2. Коэффициент сопротивления трения летательного аппарата

2.2.1. Общие сведения о сопротивлении трения

Сопротивление трения ЛА определяется суммой трения отдельных его частей с учётом их взаимного влияния. Формула для определения коэффициента сопротивления трения имеет вид

(2.5)

где , и – коэффициенты сопротивления изолированных корпуса (фюзеляжа) и несущих поверхностей.

При расчете коэффициентов сопротивления трения изолированных частей используется методика ЦАГИ, согласно которой сопротивление трения любого удобообтекаемого тела (например, несущей поверхности) определяется через сопротивление трения плоской пластинки. Согласно этой методике,

. (2.6)

З

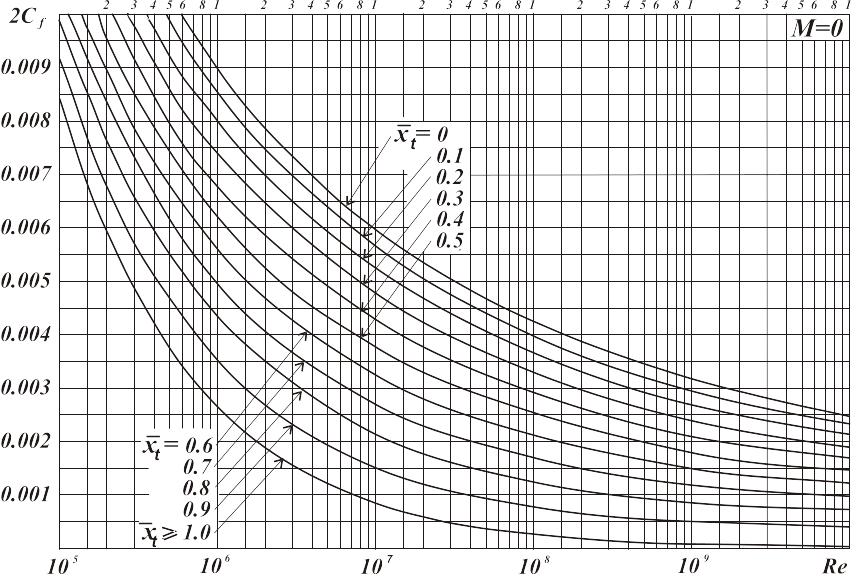
Рис. 2.1. График зависимости удвоенного коэффициента трения плоской пластинки от числа и значения при

десь – коэффициент сопротивления трения одной стороны плоской пластинки в несжимаемом потоке ( ) при одинаковых с данным телом числе Рейнольдса и положении точки перехода ламинарного пограничного слоя в турбулентный . Удвоенное значение коэффициента учитывает обтекание пластинки с двух сторон. График зависимости приведен на рис. 2.1.

Коэффициент учитывает влияние сжимаемости (числа ) на сопротивление трения плоской пластинки, а коэффициент – влияние градиента давления (формы тела) на сопротивление трения.

Приведенные данные соответствуют гладким поверхностям. Реальные ЛА всегда имеют шероховатую поверхность, зависящую от технологии процесса её обработки. Шероховатость поверхности турбулизирует пограничный слой, т. е. смещает точку перехода к носику тела. Однако по мере роста числа это влияние становится менее заметным. Поэтому при увеличении числа требования к чистоте поверхности могут быть значительно снижены практически без ущерба для аэродинамических характеристик ЛА. Здесь речь идёт об увеличении шероховатости в разумных пределах.

Число рассчитывается по параметрам потока перед обтекаемым телом и характерному размеру этого тела :

, (2.7)

где функция ( – скорость звука, – кинематический коэффициент вязкости) определяется для заданной высоты полёта через параметры стандартной атмосферы. Значения (её размерность м^-1) для ряда высот приведены в табл. 2.1.

Таблица 2.1

,	0	2	4	6	8	10	12	14	16	18	20
	2,330	1,939	1,601	1,310	1,061	0,850	0,647	0,473	0,345	0,252	0,184

Значения функции при удовлетворительно аппроксимирует следующая формула:

, (2.8)

где – высота полёте, .

Влияние числа на коэффициент трения показано на рис. 2.2.

О

Рис. 2.2. Коэффициент, учитывающий влияние числа на коэффициент трения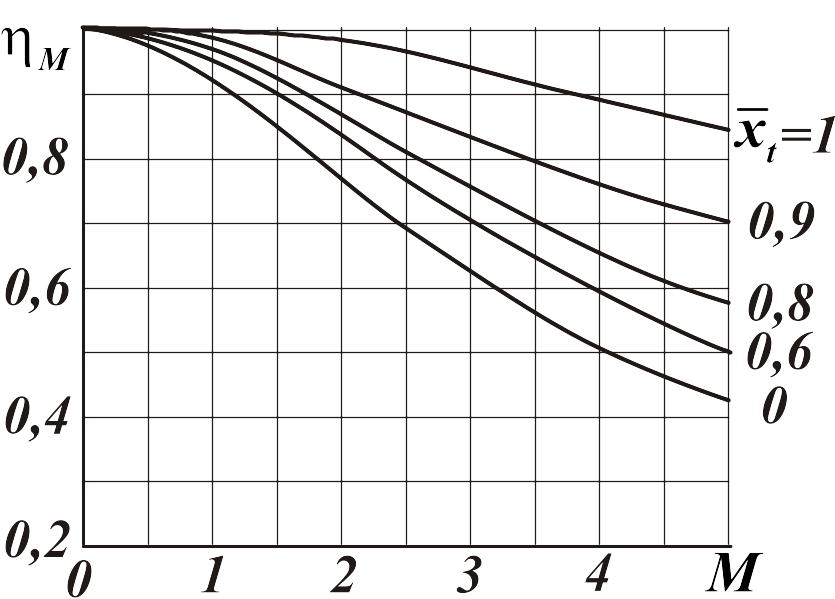

пределение точного положения точки перехода ламинарного пограничного слоя в турбулентный даже для изолированных частей ЛА довольно затруднительно. Это объясняется частично тем, что на положение точки перехода оказывают влияние многие факторы (числа и , чистота поверхности, градиент давления вдоль тела, явления теплообмена и т. п.), систематические исследования по которым пока отсутствуют. Кроме того, положения точек перехода, определённые для изолированных частей, могут сильно измениться при установке этих частей на ЛА, т. е. положение зон перехода также сильно зависит от компоновки ЛА и режима полёта.

Например, при сверхзвуковой скорости полёта и малом угле атаки из мест стыка передних кромок несущих поверхностей с корпусом выходит скачок уплотнения, «соприкасающийся» с поверхностью корпуса по двум линиям. Резкое увеличение давления за скачком уплотнения стремится вызвать переход ламинарного пограничного слоя в турбулентный вдоль этих линий. При увеличении угла атаки давление на верхней поверхности снижается и этот переход может не произойти. Следует отметить, что положение зоны перехода зависит также от характера движения, наличия тряски и других причин и может быть определено только на основании экспериментальных данных.

При аэродинамическом расчёте на начальном этапе проектирования допустимо считать, что на всех элементах конструкции ЛА формируется турбулентный пограничный слой ( ). В этом случае величина сопротивления трения ЛА получается несколько завышенной, что создаёт некоторый «гарантийный запас» в получении требуемых лётных характеристик.

Для расчёта коэффициента сопротивления трения при турбулентном пограничном слое ( ) можно воспользоваться следующими формулами:

при ; (2.9)

при . (2.10)

Для определения этих величин при известном положении зоны перехода необходимо пользоваться графиками, приведенными на рис. 2.1 и 2.2.

Следует заметить, что представленные формулы и графики справедливы только при отсутствии теплообмена между средой и телом. При наличии теплопередачи можно использовать приближенный метод расчета сопротивления трения, представленный в работе [7].