Раздел третий

ДЕТАЛИ МАШИН

ОСНОВНЫЕ ПОНЯТИЯ О ПЕРЕДАЧАХ

Назначение передач и их классификация

Механическими передачами называют механизмы, передающие работу двигателя исполнительному органу машины.

В зависимости от принципа действия все механические передачи делятся на две группы: передачи трением – фрикционные и ремённые; передачи зацеплением – зубчатые, червячные, цепные.

В зависимости от способа соединения ведущего и ведомого звеньев бывают: передачи непосредственного контакта – фрикционные, зубчатые, червячные; передачи гибкой связью – ремённые, цепные.

Основные силовые и кинематические соотношения

Основные характеристики передачи: мощность на ведущем P₁ и ведомом P₂ валах, угловая скорость ведущего ω₁ и ведомого ω₂ валов (рис. 1).

Рис. 1. Схема для определения направления вращающих моментов в передаче: а – колёса в рабочем положении; б – колёса, условно раздвинутые.

Дополнительные характеристики:

- механический к.п.д.

η = P₂/ P₁;

- общий к.п.д.

η_общ = η₁ η₂… η_n,

где η₁ η₂… η_n - к.п.д. каждой кинематической пары (зубчатой, червячной, ременной и других передач подшипников, муфт);

- окружная скорость:

v = ωd/2,

где d - диаметр колеса, шкива и др.

- окружная сила:

F_t = P/v = 2T/d,

- вращающий момент:

T = P/ω = F_t d/2,

Передаточным отношением называется отношение уголовых скоростей ведущего и ведомого звеньев. В передаче, понижающей угловые скорости u>1, при u<1 угловые скорости повышаются.

Для многоступенчатой передачи общее передаточное число

u_общ = u₁u₂…u_n,

где u₁u₂…u_n - передаточные числа каждой ступени.

ЦИЛИНДРИЧЕСКИЕ ПРЯМОЗУБАЯ И КОСОЗУБАЯ ПЕРЕДАЧИ

Общие сведения о прямозубых передачах

Прямозубые передачи показаны на рис. 2.

Рис. 2. Прямозубые передачи.

В прямозубой передаче зубья входят в зацепление сразу по всей длине. Передаточное число

u = ω₁/ω₂ = d₂/d₁.

Для зубчатых передач отношение числа зубьев колеса z₂ к числу зубьев шестерни z₁ также называется передаточным числом u

u = z₂/z₁.

Размеры зубчатого колеса выражают через модуль и число зубьев.

Делительный и начальный диаметры

d = d_ω = mz.

Диаметр вершин

d_a = d + 2h_a = d + 2m.

Диаметр впадин

d_f = d – 2h_f = d – 2,5m.

Межосевое расстояние

a_ω = (d₁ + d₂)/2 = d₁(u + 1)/2 = mz₁(u + 1)/2 = mz_Σ /2,

где z_Σ = z₁ + z₂ - суммарное число зубьев;

m = p/π.

Зная z_Σ, определяют число зубьев шестерни

z₁ = z_Σ /(u+1)

и колеса

z₂ = z_Σ - z₁.

Силы в зацеплении прямозубых передач

Силы взаимодействия между зубьями определяют в полюсе зацепления П (рис. 3).

Рис. 3. Схема сил в прямозубой цилиндрической передаче.

Распределенную по контактным линиям нагрузку в зацеплении заменяют равнодействующей F_n, которая направлена по линии давления (зацепления) NN. Для расчета зубьев, валов и опор силу F_n раскладывают на составляющие:

окружная сила

F_t = F_n cos α_ω = 2T₂/d₂ = T₂(u + 1)/(a_ωu);

радиальная сила

F_r = F_t tg α_ω,

где T₂ - вращающий момент на колесе;

α_ω - угол зацепления.

Расчёт на контактную прочность прямозубых передач

Наибольшее контактное напряжение в зоне зацепления определяют по формуле Герца:

,

где Е_пр = 2Е₁Е₂/(Е₁ + Е₂) - приведенный модуль упругости;

Е₁ и Е₂ - модули упругости материала шестерни и колеса;

μ - коэффициент Пуассона;

q - нормальная нагрузка на единицу длины контактной линии зуба.

Формула проверочного расчёта цилиндрических прямозубых передач

.

Формула проектного расчёта цилиндрических прямозубых передач:

,

где а_ω - межосевое расстояние;

Т₂ - вращающий момент на валу колеса;

σ_Н - допускаемое контактное напряжение;

ψ_а = b₂/a_ω - коэффициент ширины венца колеса;

b₂ – ширина венца колеса;

K_Hβ - коэффициент неравномерности нагрузки по длине зуба, зависит от коэффициента ψ_d = b₂/d₁ = 0,5ψ_a(u + 1);

K_Hv - коэффициент динамической нагрузки.

Расчёт на изгиб прямозубых передач

Формула для проверочного расчета прямозубых передач:

,

где b=b₂ - ширина венца колеса;

K_Fβ - коэффициент неравномерности нагрузки;

K_Fv - коэффициент динамической нагрузки;

Y_F - коэффициент формы зуба.

Основные геометрические соотношения косозубых передач

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном цилиндре, называют косозубыми (рис. 3). В косозубой передаче зубья входят в зацепление постепенно. У пары сопряженных косозубых колес с внешним зацеплением углы β равны, но противоположны по направлению. Одно колесо левое, другое - правое.

Рис. 3. Косозубая передача.

У косозубого колеса расстояние между зубьями можно измерить в торцовом (рис. 4), или окружном (t-t), и нормальном (n-n) направлениях. В первом случае получим окружной шаг p_t , во втором - нормальный шаг р. Различными в этих направлениях будут и модули зацепления:

m_t = p_t /π; m = p/π,

где m_t и m - окружной и нормальный модули зубьев.

Согласно рис. 4

p_t = p/cos β,

следовательно,

m_t = m/cos β,

где β - угол наклона зуба на делительном цилиндре.

Рис. 4. Геометрические размеры косозубого колеса.

Делительный и начальный диаметры

d = d_ω = m_t z/cos β.

Высоты головки зуба h_a и ножки h_f соответственно равны:

h_a = m; h_f = 1,25m.

Диаметр вершин

d_a = 2m.

Межосевое расстояние

a_ω = (d₁ + d₂)/2 = m(z₁ + z₂)/2 cos β = mz_Σ /2 cos β.

Силы в зацеплении

В косозубой передаче нормальная сила F_n составляет угол β с торцом колеса (рис. 5). Разложив F_n на составляющие, получим:

окружную силу

F_t = 2T₂/d₂;

радиальную силу

F_r = F_t tg α_ω /cos β;

осевую силу

F_a = F_t tg β.

Рис. 5. Схема сил в косозубой передаче

Расчёт на контактную прочность косозубых передач

Проектный расчет. Межосевое расстояние для косозубой пары

.

Проверочный расчет. Контактные напряжения

,

где K_Нα - коэффициент, учитывающий распределение нагрузки между зубьями,

K_Нβ - коэффициент неравномерности нагрузки по ширине венца;

K_Hv - коэффициент динамической нагрузки.

Расчёт на изгиб косозубых передач

Условия прочности на изгиб зубьев шестерни и колеса косозубой передачи

где Y_F -коэффициент формы зуба;

Y_β = 1 – β/140° - коэффициент, учитывающий наклон зуба;

K_Fα - коэффициент, учитывающий распределение нагрузки между зубьями;

K_Fβ - коэффициент, учитывающий распределение нагрузки;

K_Fv - коэффициент, учитывающий динамическую нагрузку в зацеплении.

 

КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

Общие сведения

Конические зубчатые колеса применяют в передачах, когда оси валов пересекаются под углом Σ = 90°. Конические колеса бывают с прямыми и круговыми зубьями.

Конические колёса с круговыми зубьями по сравнению с прямозубыми колёсами обладают большей несущей способностью, работают плавно и с меньшим шумом. Рекомендуется принимать β = 35° (рис. 1.).

Рис. 1. Нарезание кругового зубчатого колеса резцовой головкой: 1-заготовка; 2-воображаемое колесо, зубьями которого являются резцы 3 головки.

Сопряжённые колёса с круговым зубом имеют правое и левое направление линий зубьев. В конических передачах шестерня имеет консольное расположение на валу (рис. 2).

Рис. 2. Подшипниковый узел вала конической шестерни: 1-стакан; 2-набор металлических прокладок для регулирования зацепления.

Геометрия зацепления колёс

Роль начальных и делительных цилиндров цилиндрических зубчатых передач играют начальные и делительные конусы. При вращении колес начальные конусы катятся друг по другу без скольжения (рис. 3). Углы делительных конусов обозначают соответственно δ₁ и δ₂.

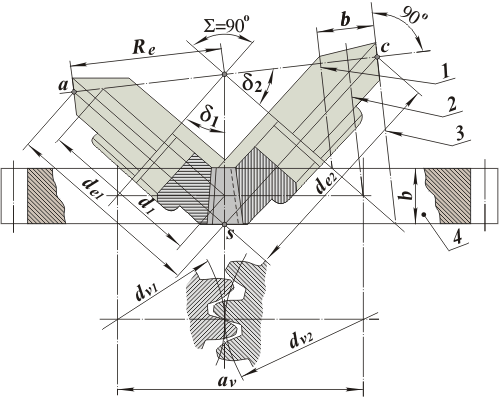
Рис. 3. Схема к геометрии зацепления конических колёс: 1, 2, 3-образующие внутреннего, среднего и внешнего дополнительных конусов; 4-эквивалентное колесо.

Зубья конических колес в зависимости от изменения размеров сечений по длине выполняются трех форм:

форма I - пропорционально понижающиеся зубья. Вершины конусов делительного диаметра и впадин совпадают (рис. 4).

Рис. 4. К геометрическому расчёту конического колеса.

форма II - понижающиеся зубья. Вершины конусов делительного диаметра и впадин не совпадают;

форма III - равновысокие зубья. Образующие конусов делительного диаметра, впадин и вершин параллельны.

Внешний окружной модуль получается по внешнему торцу колеса. Он обозначается: m_e - для прямозубых колёс и m_te - для колёс с круговыми зубьями.

Эквивалентное колесо

Из треугольника OCS (рис. 5) делительный диаметр эквивалентного колеса

d_ve = d_e /cos δ = m_e z /cos δ = m_ez_v ,

откуда эквивалентное число зубьев

z_v = z /cos δ.

Рис. 5. Схема для определения эквивалентного числа зубьев.

Для передачи с круговыми зубьями

z_v = z /(cos δ · cos³ β),

где z - действительное число зубьев конических колес.

Силы в зацеплении

Силы в конической передаче определяют по размерам средних сечений зубьев, в которых лежит точка приложения силы F_n , действующей перпендикулярно поверхности зуба. Силу F_n раскладывают на составляющие силы F_t , F_r и F_a .

Рис. 6. Схема сил в конической прямозубой передаче.

В прямозубой передаче окружная сила на шестерне или колесе

F_t = 2T₂ /d₂ = 2T₂ / (0,857 d_e2).

Радиальная сила на шестерне

F_r1 = F_t tg α_ω cos δ₁ = 0,36 F_t cos δ₁.

Осевая сила на шестерне

F_a1 = F_t tg α_ω sin δ₁ = 0,36 F_t sin δ₁.

Силы на колесе соответственно равны:

F_r2 = F_a1; F_a2 = F_r1.

В передаче с круговым зубом:

окружная сила на шестерне или колесе

F_t = 2T₂ /d₂ = 2T₂ /(0,857 d_e2);

радиальная сила на шестерне

F_r1 = F_t (0,44 cos δ₁ – 0,7 sin δ₁;

осевая сила на шестерне

F_a1 = F_t (0,44 sin δ₁ + 0,7 cos δ₁).

Силы на колесе соответственно равны:

F_r2 = F_a1; F_a2 = F_r1.

Расчёт на контактную прочность

Проверочный расчёт:

,

где - коэффициент вида конических колес;

K_Нβ - коэффициент, учитывающий распределение нагрузки по ширине венца при ;

K_Hv - коэффициент динамической нагрузки.

Проектный расчёт:

,

где d_e2 - внешний делительный диаметр колеса.

Расчёт на изгиб

Расчетные напряжения изгиба в зубьях конических колес и условие их прочности

где m_e или m_te - внешние окружные модули;

Y_F - коэффициент формы зуба эквивалентного колеса с учетом коэффициента смещения х;

- коэффициент вида конических колес;

K_Fβ - коэффициент, учитывающий распределение нагрузки по ширине венца при ;

K_Fv - коэффициент динамической нагрузки.

Расчёт на прочность

- внешний делительный диаметр d_e2

;

- ширина зубчатого венца

b = ψ_d d₁ = 0,857 ψ_d d_e2 /u;

- внешний окружной модуль передачи m_e или m_te

.

ПЕРЕДАЧА ВИНТ-ГАЙКА

Передача винт-гайка служит для преобразования вращательного движения в поступательное. При этом гайка и винт могут иметь либо одно из названных движений, либо оба движения вместе.

Расчёт передачи

Расчет передачи на износостойкость:

р_изн = F/(Az) = F/(πd₂hz)≤[р_изн],

где F - осевая сила;

А - площадь рабочей поверхности витка;

d₂ - средний диаметр резьбы;

h - рабочая высота профиля;

z - число витков в гайке высотой Н;

z = H/h;

р - шаг резьбы.

Формула для проектного расчета передачи:

,

где ψ_Н = Н/d₂ - коэффициент высоты гайки;

ζ - коэффициент рабочей высоты профиля резьбы.

Наружный диаметр гайки

,

где F_расч = 1,3F₀,

F₀ - сила затяжки болта.

Диаметр буртика гайки

.

Сильно нагруженные винты проверяют на прочность по гипотезе энергии формоизменения:

,

где σ_Е - эквивалентное напряжение для опасной точки винта;

N и M_k - продольная сила и крутящий момент, возникающие в проверяемом поперечном сечении винта;

d₁ - внутренний диаметр резьбы.

Сжатые винты проверяют на устойчивость

s_у = σ_кр /σ ≥ [s_у],

где s_у - расчетный коэффициент запаса устойчивости;

- расчетное напряжение в поперечном сечении винта;

σ_кр - критическое напряжение, возникающее в поперечном сечении винта.

ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ

Общие сведения

Червячные передачи (рис. 1) применяют для передачи вращательного движения между валами, у которых угол скрещивания осей составляет θ = 90°. Параметрам червяка приписывается индекс 1, а параметрам колеса — индекс 2.

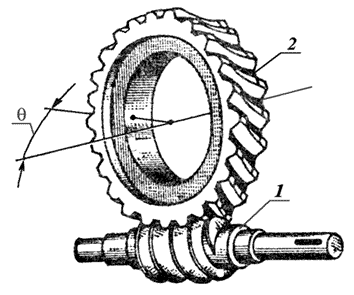
Рис. 1. Червячная передача: 1 – червяк; 2 – венец червячного колеса.

Червячная передача – это зубчато-винтовая передача, движение в которой осуществляется по принципу винтовой пары.

Достоинства:

- плавность и бесшум­ность работы;

- компактность и сравнительно небольшая масса конструкции;

- возможность большого получения больших передаточных чисел;

- возможность получения самотормозящей передачи.

Недостатки:

- сравнительно низкий к. п. д. вследствие скольжения витков червяка по зубьям колеса;

- значительное выделение теплоты в зоне зацепления червяка с колесом;

- необходимость применения для венцов червячных колес антифрикционных материалов;

- повышенное изнашивание зубчатой пары.

Классификация передачи

В зависимости от формы внешней поверхности червяка передачи бывают с цилиндрическим (рис. 2, а) или с глобоидным (рис. 2, б) червяком.

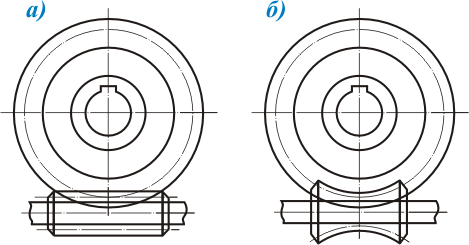
Рис. 2. Схемы червячных передач.

В зависимости от направления линии витка червяка червячные передачи бывают с правым и левым направлением линии витка. В зависимости от числа витков червяка передачи бывают с одновитковым или с многовитковым червяком. В зависимости от расположения червяка относительно колеса передачи бывают с нижним (а), боковым (б) и верхним (в) червяками (рис. 3).

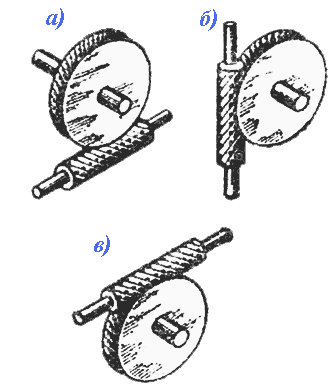
Рис. 3. Виды червячных передач.

В зависимости от формы винтовой поверхности резьбы цилиндрического червяка передачи бывают с архимедовым (рис. 4) и эвольвентным (рис. 5) червяками.

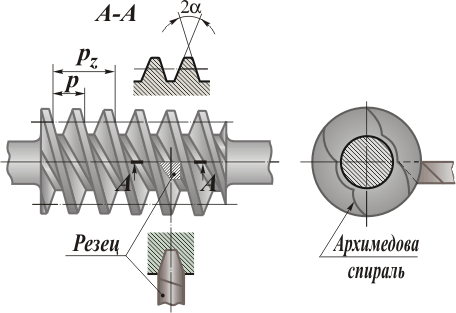
Рис. 4.

Рис. 5.

Основные геометрические соотношения

В червячной передаче расчетным является осевой модуль червяка m, равный торцовому модулю червячного колеса.

Основными геометрическими размерами червяка являются (рис. 6):

- угол профиля витка в осевом сечении 2α = 40°;

- расчетный шаг червяка p = πm;

- расчетный модуль m = p/π;

- ход витка (рис. 7) p_z = pz₁, где z₁ - число витков червяка;

- высота головки витка червяка и зуба колеса h_a1 = h_a2 = m;

- высота ножки витка червяка и зуба колеса h_f1 = h_f2 = 1,2m;

- делительный диаметр червяка d₁= qm, где q — число модулей в делительном диаметре червяка, или коэффициент диаметра червяка.

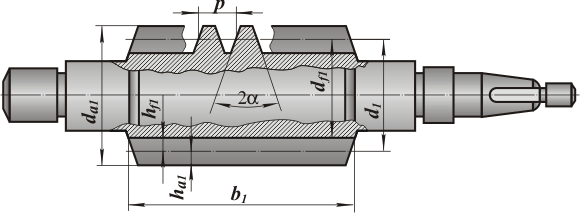
Рис. 6. Основные размеры цилиндрического червяка.

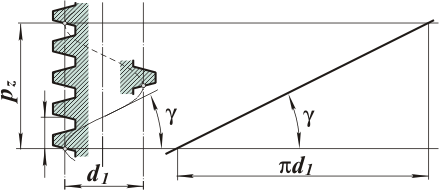
Рис. 7. Схема определения делительного угла подъёма линии витка.

Делительный угол подъема линии витка:

tg γ = p_z /πd₁ = z₁ /q.

Диаметр вершин витков:

d_a1 = d₁ + 2h_a1 = m(q + 2).

Диаметр впадин витков:

d_f1 = d₁ – 2h_f1 = m(q – 2,4).

Длина нарезанной части:

b₁ ≥ (c₁ + c₂ z₂)m,

где z₂ - число зубьев колеса;

коэффициенты c₁ и c₂ зависят от коэффициента смещения инструмента х.

Коэффициент смещения инструмента:

x = a_ω /m – 0,5(q + z₂).

Основные геометрические размеры венца червячного колеса (рис. 8) определяют в среднем его сечении. К ним относятся:

делительный диаметр

d₂ = mz₂;

диаметр вершин зубьев

d_a2 = m(z₂ + 2 + 2x);

диаметр впадин колеса

d_f2 = m(z₂ – 2,4 + 2x);

межосевое расстояние передачи

a_ω = 0,5m(q + z₂ + 2x);

наибольший диаметр червячного колеса

d_aM2 ≤ d_a2 + 6m /(z₁ + 2);

ширина венца червячного колеса зависит от диаметра вершин витков червяка: при z₁ =1...2

b₂ ≤ 0,75 d_a1,

при z₁ = 4

b₂ ≤ 0,67 d_a1;

условный угол обхвата червяка колесом

sin δ = b₂ /(d_a1 – 0,5m).

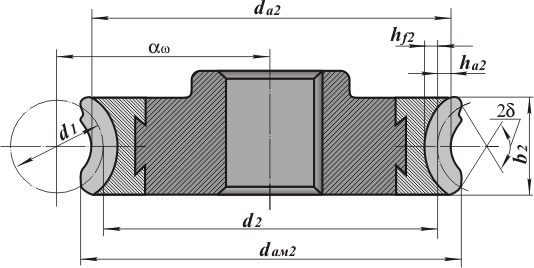
Рис. 8.

Скорость скольжения в передаче

Скорость скольжения v_s направлена по касательной к винтовой линии делительного цилиндра червяка и определяется из параллелограмма скоростей (рис. 9)

v_s = v₁ /cos γ = ω₁d₁ /(2 cos γ) = uω₂d₁ /(2 cos γ),

где v₁ и v₂ - окружные скорости червяка и колеса.

Рис. 9. Схема определения скорости скольжения в червячной передаче.

Силы в зацеплении

Силу взаимодействия червяка и колеса F_n (рис. 10, а) принимают сосредоточенной и приложенной в полюсе зацепления П по нормали к рабочей поверхности витка. По правилу параллелепипеда F_n раскладывают по трем взаимно перпендикулярным направлениям на составляющие F_t1, F_r1, F_a1. Для ясности изображения сил на рис. 11, б червячное зацепление раздвинуто. Окружная сила на червячном колесе F_t2 численно равна осевой силе на червяке

F_a1:F_t2 = F_a1 = 2T₂ /d₂,

где T₁ - вращающий момент на червячном колесе.

Рис. 10. Схема сил, действующих в червячном зацеплении.

Окружная сила на червяке F_t2 численно равна осевой силе на червячном колесе F_a2:

,

где T₁ - вращающий момент на червяке;

η - к. п. д. передачи.

Радиальная сила на червяке F_r1 численно равна радиальной силе на колесе F_r2 (рис. 10, в):

F_r1 = F_r2 = F_t2 tg α.

Направление силы F_t2 совпадает с направлением вращения колеса, а сила F_t1 направлена в сторону, противоположную вращению червяка (рис. 11, г).

Допускаемые напряжения для материалов венцов червячных колёс

Допускаемые контактные напряжения определяют из условия сопротивления усталостному износу рабочих поверхностей зубьев:

[σ]_H = K_HL C_v [σ]_H0,

где - коэффициент долговечности при расчете на контактную прочность;

N_Σ - число циклов нагружения зубьев червячного колеса за весь срок службы передачи;

C_v - коэффициент, учитывающий интенсивность изнашивания зуба колеса в зависимости от скорости скольжения;

[σ]_H0 - допускаемое контактное напряжение, соответствующее пределу контактной выносливости при числе циклов перемены напряжений 10⁷.

Расчёт на прочность

Расчёт по контактным напряжениям. Наибольшее контактное напряжение в зоне зацепления определяют по формуле Герца

,

где E_пр = 2Е₁Е₂ /(Е₁ + Е₂) - приведенный модуль упругости;

μ - коэффициент Пуассона;

q - нормальная нагрузка на единицу длины контактных линий.

Проверочный расчёт по контактным напряжениям

,

где d₁, d₂ - диаметры червяка и колеса;

T₂ - вращающий момент на червячном колесе.

Проектный расчёт по контактным напряжениям

.

Расчёт по напряжениям изгиба. Проверочный расчёт по напряжениям изгиба.

,

где σ_F - расчетное напряжение изгиба в опасном сечении зубьев червячного колеса;

Y_F2 - коэффициент формы зуба колеса, который выбирают в зависимости от эквивалентного числа зубьев z_v2 = z₂ /cos³ γ.

Тепловой расчёт

Тепловой расчет червячной передачи производится на основе теплового баланса т. е. равенства тепловыделения Q_B и теплоотдачи Q₀.

Количество теплоты, выделяющейся в непрерывно работающей передаче в одну секунду:

Q_B = (1 – η)P₁,

где η - к.п.д. червячной передачи;

P₁ - мощность на червяке.

По условию теплового баланса Q_B = Q₀, т. е.

(1 – η)Р₁ = К_Т(t_M – t_B)A,

откуда температура масла в корпусе червячной передачи

t_M = t_B + (1 – η)P₁ /(K_TA) ≤ [t]_M.

Здесь A - площадь поверхности корпуса; t_B - температура воздуха вне корпуса; t_M - температура масла в корпусе передачи; K_T - коэффициент теплопередачи.

ЦЕПНЫЕ ПЕРЕДАЧИ

Общие сведения

Цепная передача относится к передачам зацеплением с гибкой связью (рис. 1). Передача состоит из ведущей и ведомой звездочек, огибаемых цепью.

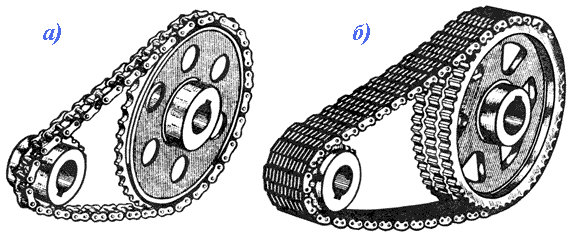
Рис. 1. Цепная передача: а – роликовой цепью; б – зубчатой цепью.

Достоинства:

- по сравнению с зубчатыми передачами цепные передачи могут передавать движение между валами при значительных межосевых расстояниях (до 8 м);

- по сравнению с ременными передачами:

а) более компактны,

б) могут передавать большие мощности (до 3000 кВт),

в) сравнительно небольшие силы, действующие на валы.

Недостатки:

- значительный шум вследствие удара звена цепи при входе в зацепление;

- сравнительно быстрое изнашивание шарниров цепи;

- удлинение цепи из-за износа шарниров.

Приводные цепи

Приводная цепь состоит из соединённых шарнирами звеньев.

Основными типами приводных цепей являются втулочные, роликовые и зубчатые.

Роликовые цепи. Состоят из двух рядов наружных и внутренних пластин (рис. 2). В наружные пластины запрессованы валики, пропущенные через втулки, на которые запрессованы внутренние пластины. Валики и втулки образуют шарниры. На втулки свободно надеты ролики. Зацепление цепи со звездочкой происходит через ролик, который перекатывается по зубу и уменьшает его износ. Кроме того, ролик выравнивает давление зуба на втулку и предохраняет ее от изнашивания.

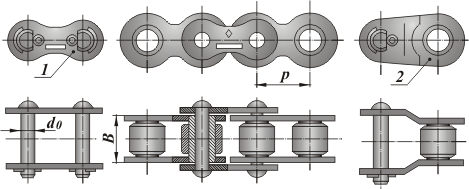
Рис. 2. Приводная роликовая однорядная цепь: 1 – соединительное звено; 2 – переходное звено.

Втулочные цепи. Эти цепи по конструкции аналогичны предыдущим, но не имеют роликов. В зависимости от передаваемой мощности втулочные и роликовые цепи изготовляют однорядными и многорядными (рис. 3). Соединение цепи при четном числе звеньев производят соединительным звеном 1, при нечетном - переходным 2.

Рис. 3. Втулочная цепь.

Зубчатые цепи. Состоят из набора пластин зубообразной формы, шарнирно соединенных между собой. Рабочими гранями пластин являются плоскости зубьев, расположенные под углом 60° (рис. 4).

Рис. 4.

Для устранения бокового спадания цепи со звездочки применяют направляющие пластины 1, расположенные по середине цепи или по бокам ее (рис. 5).

Рис. 5. Приводная зубчатая цепь.

Шарнир трения качения (рис. 6) состоит из двух призм 1 и 2 с цилиндрическими поверхностями, которые обеспечивают трение качения. Длина призм равна ширине цепи. Призма 1 закреплена в пластинах А, а призма 2 - в пластинах Б.

Рис. 6.

Звёздочки

Звездочки по конструкции отличаются от зубчатых колес лишь профилем зубьев, размеры и форма которых зависят от типа цепи (рис. 7).

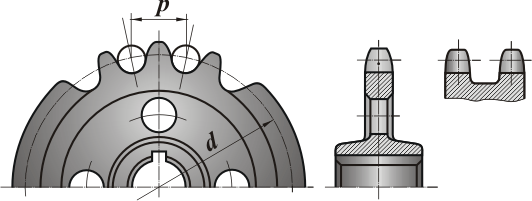
Рис. 7. Звёздочки роликовой и втулочной цепей.

Делительная окружность звездочек проходит через центры шарниров цепи. Из треугольника Оас

d = p/sin (180°/z),

где z - число зубьев звездочки (см рис. 4).

Шаг р у звездочек измеряется по хорде делительной окружности.

Число зубьев малой звездочки для втулочных и роликовых цепей принимают по эмпирической зависимости

z_1min = 29 – 2u,

где u - передаточное число.

Передаточное число цепной передачи

Цепь за один оборот звездочки проходит путь pz, следовательно, скорость цепи

v = pz₁ω₁/2π = pz₂ω₂/2π,

где р - шаг цепи;

z₁ и z₂ - числа зубьев ведущей и ведомой звездочек;

ω₁ и ω₂ - угловые скорости ведущей и ведомой звездочек.

Из равенства скоростей цепи на звездочках передаточное число

u = ω₁/ω₂ = z₂/z₁.

Основные геометрические соотношения в цепных передачах

Межосевое расстояние передачи (рис. 8)

а = (30...50)p,

где р - шаг цепи.

Рис. 8. Схема цепной передачи.

Длина цепи

,

где l_p - длина цепи в шагах или число звеньев цепи.

Межосевое расстояние передачи при окончательно выбранном числе шагов

.

Сила в ветвях цепи

Окружная сила:

F_t = 2T/d,

где d - делительной диаметр звездочки.

Предварительное натяжение цепи

F₀ = k_f qag,

где k_f - коэффициент провисания;

q - масса 1 м цепи;

а - межосевое расстояние;

Натяжение цепи от центробежных сил

F_v = qv².

Сила F_v нагружает звенья цепи по всему ее контуру, но звездочками не воспринимается (рис. 9) .

Рис. 9. Эпюра сил в звеньях при работе передачи.

Натяжение ведущей ветви цепи работающей передачи

F₁ = F_t + F₀ + F_v .

Натяжение ведомой ветви цепи F₂ равно большему из натяжений F₀ и F_v .

Нагрузка на валы звёздочек. Цепь действует на валы звездочек с силой

F_n = k_BF_t + 2F₀ ,

где k_B - коэффициент нагрузки вала.

Расчёт цепной передачи на износостойкость

Расчет передачи с роликовой (втулочной) цепью. Нагрузочная способность цепи определяется из условия, чтобы среднее давление р_ц в шарнире звена не превышало допускаемого [р_ц]:

р_ц = F_tK_э /A ≤ [р_ц],

где F_t - окружная сила, передаваемая цепью;

А - площадь проекции опорной поверхности шарнира, для роликовых (втулочных) цепей A = d₀B;

d₀ - диаметр оси;

В - длина втулки;

K_э - коэффициент эксплуатации, K_э = K_ДK_сK_θK_р,

K_Д - коэффициент динамичности нагрузки;

K_с - коэффициент способа смазывания;

K_θ - коэффициент наклона линии центров звездочек к горизонту;

K_р - коэффициент способа регулирования натяжения цепи.

Выразив в формуле р_ц = F_tK_э /A ≤ [р_ц] окружную силу F_t через момент T₁ на малой звездочке, шаг цепи р и число зубьев z₁, а площадь проекции опорной поверхности шарниров через шаг р, получим формулу для предварительного выбора шага роликовой (втулочной) цепи:

,

где v - число рядов роликовой (втулочной) цепи;

[р_ц] - допускаемое давление в шарнирах роликовой цепи.

Расчёт передачи с зубчатой цепью. Особенности выбора зубчатых цепей заключатся в том, что для одного шага р цепи существует пять или шесть стандартных ширин B цепи. Шаг цепи р выбирают в зависимости от максимально допустимой угловой скорости ω_1max меньшей звездочки. Число зубьев z₁ меньшей звездочки определяют по формуле z_1min = 29 – 2u.

Исходя из критерия износостойкости шарнира зубчатой цепи по известным Р, р и v вычисляют требуемую ширину В цепи:

,

где K_v - скоростной коэффициент, учитывающий снижение несущей способности цепи из-за центробежных сил K_v = 1-1,1·10^-3v².

РЕМЁННЫЕ ПЕРЕДАЧИ

Общие сведения

Ременная передача относится к передачам трением с гибкой связью. Такая передача состоит из ведущего и ведомого шкивов, огибаемых ремнем (рис. 1). В зависимости от формы поперечного сечения ремня передачи бывают: плоскоременные (рис. 2, а), клиноременные (рис. 2, б), круглоременные (рис. 2, в), поликлиноременные (рис. 2, г).

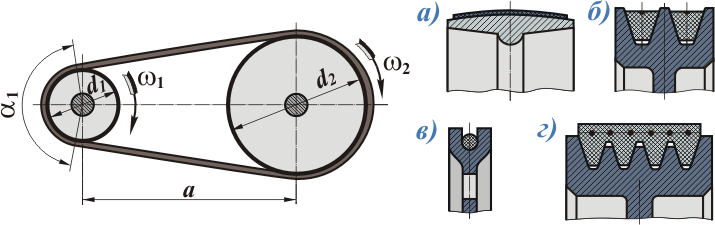
Рис. 1. Схема ремённой передачи.

Рис. 2. Формы поперечного сечения ремня.

Основные геометрические соотношения ремённых передач

- межосевое расстояние (рис. 3).

для плоскоременных передач

a ≥ 1,5(d₂ + d₁);

для клиноременных и поликлиноременных передач

a ≤ 0,55(d₂ + d₁) + h;

где d₁, и d₂ - диаметры шкивов;

h - высота сечения ремня.

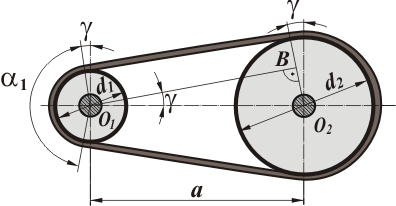
Рис. 3. Геометрические параметры ремённой передачи.

- расчетная длина ремня

l = 2a + π(d₂ + d₁)/2 + (d₂ – d₁)²/4a;

- межосевое расстояние при окончательно установленной длине ремня

;

- угол обхвата ремнем малого шкива

α₁ = 180° - 2γ.

или

α₁ = 180° - 57° (d₂ – d₁) / a.

Для плоскоременной передачи рекомендуется |α₁| ≥ 150°, а для клиноременной и поликлиноременной | α₁| ≥ 120°.

Силы в передаче

Для создания трения между ремнем и шкивом ремню после установки на шкив создают предварительное натяжение F₀. (рис. 3, а). При приложении рабочей нагрузки T₁ происходит перераспределение натяжений в ветвях ремня: ведущая ветвь дополнительно натягивается до силы F₁, а натяжение ведомой ветви уменьшается до F₂ (рис. 3, б). Из условия равновесия моментов внешних сил относительно оси вращения

F₁ – F₂ = F_t ,

где F_t = 2T₁ / d₁ - окружная сила на шкиве.

Рис. 3. Силы в ветвях ремня.

F₁ + F₂ = 2F₀.

Решая совместно уравнения F₁ – F₂ = F_t и F₁ + F₂ = 2F₀, получаем

F₁ = F₀ + F_t /2; F₂ = F₀ – F_t /2.

При обегании ремнем шкивов в ремне возникает центробежная сила

F_v = ρAv²,

где А - площадь сечения ремня;

ρ- плотность материала ремня.

Натяжение в ведущей и ведомой ветвях передачи

F₁ + F_v , F₂ + F_v ;

для холостого хода

F₀ + F_v .

Нагрузка на валы и подшипники. Силы натяжения ветвей ремня нагружают валы и подшипники. Из треугольника Оаb равнодействующая сила F_n = 2F₀ sin (α₁ / 2) (рис. 4).

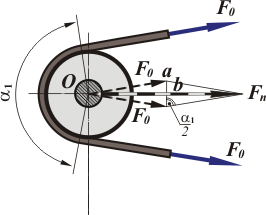
Рис. 4. К определению нагрузки на валы ремённой передачи.

Скольжение ремня. Передаточное число.

В ременной передаче возникают два вида скольжения ремня по шкиву: упругое - при нормальной работе передачи и буксование - при перегрузке.

В процессе обегания ремнем ведущего шкива натяжение его падает от F₁ до F₂ (рис. 5). Ремень укорачивается и отстает от шкива - возникает упругое скольжение. На ведомом шкиве происходит аналогичное скольжение, но здесь натяжение ремня возрастает от F₂ до F₁, он удлиняется и опережает шкив. Упругое скольжение ремня происходит не на всей дуге обхвата, а лишь на части её – дуге скольжения α_c .

Рис. 5. Скольжение в ремённой передаче.

Со стороны набегания ремня на шкив имеется дуга покоя α_п. Сумма дуг α_c и α_п равна дуге обхвата α.

Упругое скольжение ремня характеризуется коэффициентом скольжения ξ:

ξ = (v₁ – v₂) / v₁,

где v₁ и v₂ - окружные скорости ведущего и ведомого шкивов.

Передаточное число ременной передачи:

u = ω₁ / ω₂ = d₂ / [d₁ (1 – ξ)],

где ω₁ и ω₂ - угловые скорости ведущего и ведомого шкивов.

Напряжения в ремне

При работе ременной передачи напряжения по длине ремня распределяются неравномерно. Различают следующие виды напряжения в ремне (рис. 6):

Рис. 6. Эпюра напряжений в ремне при работе передачи.

1. Предварительное напряжение

σ₀ = F₀ / A,

где А - площадь поперечного сечения ремня.

2. Удельная окружная сила

k_п = F_t / A.

3. Напряжение изгиба. Возникает в ремне при огибании шкивов (рис. 7). По закону Гука

σ_и = εE,

где ε = y_max / r - относительное удлинение волокон на выпуклой стороне ремня при изгибе;

y_max = 0,5 δ;

r = 0,5 (d + δ), следовательно,

σ_и = εE / (d + δ).

Рис. 7. К изгибу ремня на шкиве.

Пренебрегая значением δ по сравнению с d, получаем

σ_и = εE / d,

где δ - толщина ремня;

Е - модуль продольной упругости материала ремня.

4. Напряжение от центробежных сил

σ_v = F_v / A.

Плоскоременная передача

Расчёт плоскоремённой передачи. Расчет по тяговой способности плоскоременной передачи сводится к определению ширины сечения ремня b из условия

F_t ≤ δ b [k_п],

где F_t, δ и [k_п] - соответственно окружная сила, толщина ремня и допускаемая удельная окружная сила.

Разделив обе части равенства [F_t] = 2φ₀F₀ на площадь поперечного сечения ремня А, получим

[k₀] = 2φ₀σ₀,

где [k₀] - допускаемая приведенная удельная окружная сила в ремне;

[k_п] = [k₀]C_θC_αC_vC_pC_dC_F,

где C_θ - коэффициент угла наклона линии центров шкивов к горизонту;

C_α - коэффициент угла обхвата;

C_v - коэффициент влияния натяжения от центробежной силы;

C_p- коэффициент динамичности нагрузки и длительности работы;

C_d - коэффициент влияния диаметра меньшего шкива;

C_F - коэффициент неравномерности распределения нагрузки между нитями ремня.

Клиноремённая передача

Расчет передач с клиновыми и поликлиновыми ремнями. Допускаемая мощность, передаваемая одним ремнем или одним клином:

[Р_п] = [P₀]C_αC_lC_pC_z ,

где C_α - коэффициент, учитывающий влияние угла обхвата на тяговую способность ремня;

C_l - коэффициент, учитывающий влияние на долговечность длины ремня;

C_p - коэффициент динамичности нагрузки и режима работы;

C_z - коэффициент, учитывающий число ремней в комплекте.

Число клиновых ремней в комплекте или число клиньев в поликлиновом ремне передачи

z = P₁ / [Р_п] ≤ [z],

где P₁ - передаваемая мощность на валу малого шкива.

Сила предварительного натяжения ветвей поликлинового ремня или комплекта клиновых ремней

F₀ = 0,85P₁C₁ / (vC_αC_p).

Зубчато-ремённая передача

Расчёт зубчато-ремённой передачи. Расчет передачи ведут по допускаемой удельной окружной силе

[k_п] = [k₀]C_pC_F – qv²,

где C_p- коэффициент динамичности нагрузки и режима работы;

C_F - коэффициент, учитывающий неравномерность распределения нагрузки;

qv² - центробежная сила;

q - масса 1 м ремня;

Делительные диаметры шкивов:

d₁ = mz₁, d₂ = mz₂,

где z₁ и z₂ - числа зубьев шкивов.

Межосевое расстояние передачи

a ≥ 0,5 (d₂ + d₁).

Длина ремня в шагах (число зубьев ремня)

,

где р - шаг ремня.

Окончательное значение а при выбранной длине ремня

.

Число зубьев ремня, находящихся в зацеплении с меньшим шкивом

z₀ = z₁α₁ / 360° ≥ [z₀],

где α₁ - угол обхвата на меньшем шкиве.

Предварительное натяжение

F₀ = 1,2 bqv².

Сила, действующая на валы

F_n = 1,1 F_t.

МУФТЫ

Общие сведения

Муфты применяются для соединения валов механизмов. Использование муфт вызвано необходимостью: компенсации небольших неточностей монтажа в относительном расположении соединяемых валов; амортизации резких колебаний вращающего момента; наличие предохранительного звена; включения и выключения отдельных узлов.

Общая классификация муфт:

- соединительные;

- сцепные;

- предохранительные.

Соединительные муфты

Соединительные глухие муфты

Втулочные муфты (рис. 1) применяют в случаях, когда вал должен работать как одно целое. Такие муфты требуют точной соосности соединяемых валов. Втулочную муфту закрепляют на валу шпонками или штифтами.

Рис. 1.

Фланцевые муфты состоят из двух фланцевых полумуфт 1 и 2, установленных на концах валов и шпоночными соединениями (рис. 2). Эти муфты надёжно соединяют соосные валы и способны передавать большие моменты.

Рис. 2. Муфта фланцевая открытая.

Расчёт фланцевой муфты

Болты установлены с зазором

где Т_тр – момент трения на рабочих поверхностях;

F_з – сила затяжки одного болта;

f – коэффициент трения;

z – число болтов;

D₀ – диаметр центра болта;

d₁ – внутренний диаметр резьбы болта;

К- коэффициент затяжки.

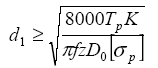
где Т_р – расчётный момент.

Болты установлены без зазора

где Т_ср – момент среза болтов;

F_t – окружная сила, срезающая болт;

d₀ – наружный диаметр стержня болта;

n – число поверхностей среза.

.

Соединительные компенсирующие муфты с подвижным элементом

Компенсирующие муфты применяют для уменьшения нагрузок на валы и опоры за счёт компенсации радиальных, осевых и угловых смещений.

Зубчатые муфты компенсируют продольные и радиальные смещения валов в пределах 1-8 мм и угловое до 1°. Зубчатая муфта состоит из двух полумуфт 1 и 2 с наружными зубьями и разъёмной обоймы 3 с двумя рядами внутренних зубьев (рис. 3).

Рис. 3. Муфта зубчатая: 1 – обойма; 2 – втулка.

Расчёт на прочность

,

где К_д - коэффициент динамичности;

F_t – окружная сила;

b, h – длина и рабочая высота зуба;

z – число зубьев;

D₀ = mz – делительный диаметр зубьев,

где ψ = 0,12…0,16.

Сила, действующая на валы

F_M ≈ (0,15…0,2)F_t.

Соединительные компенсирующие муфты с упругим элементом

Упругие втулочно-пальцевые муфты (МУВП) имеют широкое распространение в приводах электродвигателей с малыми и средними вращающими моментами (рис. 4). Деформация резиновых упругих элементов смягчает толчки и удары. МУВП компенсирует радиальное смещение до 0,6 мм, угловое до 1° и небольшое осевое смещение валов.

Рис. 4. Муфта упругая втулочно-пальцевая.

Для проверки прочности рекомендуется рассчитывать пальцы по напряжениям изгиба, а резину – по напряжениям смятия на поверхности соприкосновения втулок с пальцами.

Пальцы

,

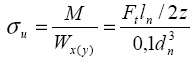где l_n – длина пальцев;

z- число пальцев;

d_n – диаметр пальцев;

D₁ – диаметр центра пальцев;

.

Втулки

,

где l_в – длина втулки;

.

Муфты упругие со звёздочкой (рис. 5) применяют для валов диаметром 12…48 мм в диапазоне крутящих моментов 6,3…400 Н∙м. Муфты такого типа допускают радиальное смещение до 2 мм, угловое до 1°30′; их применяют для соединения быстроходных валов (3000…6000 об/мин).

Рис. 5. Муфта упругая со звёздочкой.

Работоспособность резиновой звёздочки определяется напряжением смятия

,

где D – наружный диаметр звёздочки;

z – число зубьев звёздочки;

h – ширина зубьев звёздочки;

d₁ – диаметр вала.

Муфты с торообразной упругой оболочкой (рис. 6) обладают высокой податливостью, угол закручивания до 5°, могут компенсировать радиальные смещения валов до 5 мм, осевые – до 4 мм, углы поворота до 4°.

Рис. 6. Муфта с торообразной оболочкой.

Оболочку рассчитывают по напряжениям сдвига в сечении около зажима фланцами

Используя эту формулу и принятые соотношения, можно получить выражение для наружного диаметра оболочки

.

Сцепные муфты. Классификация

Сцепные муфты классифицируют:

- кулачковые (жёсткие);

- фрикционные: дисковые, конусные, колодочные.

Кулачковые муфты состоят из двух полумуфт с кулачками на торцевых поверхностях (рис. 7). Кулачки имеют профиль прямобочный, трапецеидальный и треугольный соответственно для больших, средних и малых нагрузок.

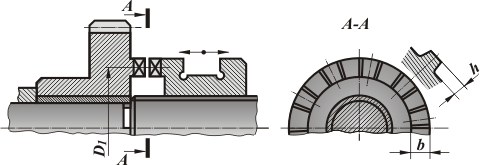
Рис. 7. Кулачковая сцепная муфта.

Расчёт на изгиб

,

где К₁ – коэффициент неравномерности распределения нагрузки по кулачкам;

z – число кулачков;

a, b, h – размеры кулачков;

D₁ – средний диаметр кулачков.

Расчёт на смятие

.

Фрикционные муфты позволяют соединять валы под нагрузкой и с большей разностью начальных угловых скоростей, так как при включении муфт вращающий момент возрастает постепенно, по мере увеличения силы давления на поверхности трения. По форме поверхностей трения фрикционные муфты делятся на дисковые (рис. 8, а), конусные (рис. 8, б) и цилиндрические (рис. 8, в).

Рис. 8. Муфты фрикционные: а – дисковая; б – коническая; в – цилиндрическая.

Многодисковая фрикционная муфта (рис. 9) состоит из двух полумуфт в виде корпуса 1 и втулки 3, дисков 4, и нажимного механизма 2. В продольные пазы на внутренней поверхности корпуса входят зубья ведущих дисков 4, а в пазы на наружной поверхности втулки – зубья ведомых дисков 5, между которыми возникают силы трения, что обуславливает передачу вращающего момента.

Рис. 9. Муфта фрикционная многодисковая: 1 – корпус; 2 – нажимной механизм; 3 – втулка; 4 – диск ведущий; 5 – диск ведомый.

Расчёт

где Т_тр – момент трения на рабочих поверхностях дисков;

β – коэффициент запаса сцепления.

где f – коэффициент трения;

Z – число пар трущихся поверхностей;

D₁, D₂ – наружный и внутренний диаметры рабочей поверхности дисков;

- средний диаметр поверхности трения дисков.

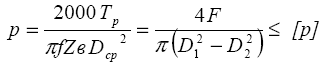
где F – общая сила нажатия на диски муфты.

где K_Z – коэффициент, учитывающий влияние числа дисков в муфте на силу включения;

.

.

Предохранительные муфты

Муфты, срабатывающие без разрушения деталей

Пружинно-кулачковая предохранительная муфта (рис. 10) При перегрузке сумма осевых составляющих сил на гранях кулачков становится больше прижимного усилия пружины и муфта многократно прощелкивает кулачками.

Рис. 10. Пружинно-кулачковая предохранительная муфта.

Фрикционные предохранительные муфты (рис. 11). Сила нажатия в них создается пружинами, отрегулированными на передачу предельного вращающего момента.

Рис. 11. Многодисковая фрикционная предохранительная муфта.

Муфты со специальным разрушающимся элементом

При возникновении перегрузок применяют предохранительные муфты со срезным штифтом (рис. 12). Штифты снабжают выточкой в предполагаемом месте разрушения.

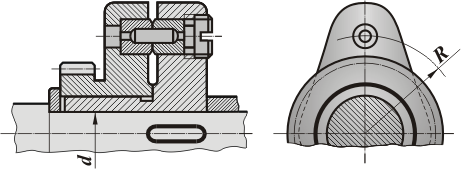
Рис. 12. Муфта предохранительная со срезным штифтом.

Диаметр штифта в месте разрушения

где K_z – коэффициент неравномерности распределения нагрузки между штифтами;

z – число штифтов;

R – радиус расположения сечения среза штифтов.

РЕЗЬБОВЫЕ СОЕДИНЕНИЯ

Образование резьбы

Резьбовые соединения являются наиболее распространенными разъемными соединениями. Их образуют болты, винты, шпильки, гайки и другие детали, снабженные резьбой. Основным элементом резьбового соединения является резьба, которая получается путем нарезания или накатки на поверхности деталей канавок по винтовой линии. Винтовую линию образует гипотенуза прямоугольного треугольника при навертывании на прямой круговой цилиндр.

Если плоскую фигуру (треугольник, трапецию и т.п.) перемещать по винтовой линии (рис. 1) так, чтобы ее плоскость при движении всегда проходила через ось винта, то эта фигура образует резьбу соответствующего профиля (рис. 2).

Рис. 1. Образование винтовой линии.

Рис. 2. Образование резьбы.

В зависимости от формы поверхности, на которой образуется резьба, различают цилиндрическую и коническую резьбу (рис. 3).

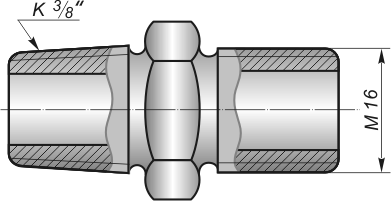
Рис. 3. Цилиндрическая и коническая резьба.

В зависимости от формы профиля резьбы делятся на пять основных типов (рис. 4): треугольные (а), упорные (б), трапецеидальные (в), прямоугольные (г) и круглые (д).

Рис. 4. Профили резьбы.

В зависимости от направления винтовой линии резьбы бывают правые и левые (рис. 5). У правой резьбы винтовая линия поднимается слева вверх направо.

В зависимости от числа заходов резьбы делятся на однозаходные и многозаходные (см. рис. 5). Многозаходные резьбы получаются при перемещении по винтовым линиям нескольких рядом расположенных профилей.

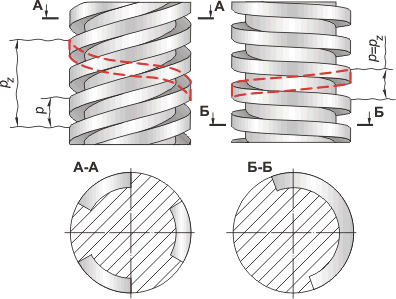
Рис. 5. Правая трёхзаходная и левая однозаходная резьба.

Геометрические параметры резьбы

Основные геометрические параметры цилиндрической резьбы (рис. 6): d - наружный диаметр; d₁ - внутренний диаметр; d₂ - средний диаметр; p - шаг резьбы; p_z - ход резьбы; α – угол профиля резьбы; γ – угол подъёма резьбы:

tg γ = p_z /(πd₂).

Рис. 6. Геометрические параметры цилиндрической резьбы.

Конструктивные формы резьбовых соединений

Основными резьбовыми соединениями являются соединения болтами, винтами и шпильками (рис. 8, а, б, в).

а) б) в)

Рис. 8. Резьбовые соединения.

Силовые соотношения в винтовой паре

Рассмотрим силы, возникающие в винтовой паре с прямоугольной резьбой (рис. 9).

Рис. 9. Схема сил в винтовой паре.

Гайка нагружена осевой силой F и, равномерно вращаясь под действием окружной силы F_t, приложенной по касательной к окружности среднего диаметра d₂ резьбы перемещается вверх. Развернем виток резьбы в наклонную плоскость, а всю гайку представим в виде ползуна. При равномерном перемещении вверх по наклонной плоскости ползун находится в состоянии равновесия под действием системы сил F, F_t, N и R_f, из которых N - нормальная реакция наклонной плоскости, а R_f = fN – сила трения.

Заменим силы N и R_f их равнодействующей R. Угол ρ между векторами сил R и N называется углом трения. Из теоретической механики известно, что tg ρ = f, где f - коэффициент трения. Проецируя систему сил на ось х-х, расположенную под углом γ + ρ к горизонтали, получим

∑Х = 0;

-F sin (γ + ρ) + F_t cos (γ + ρ) = 0,

откуда

F_t = F tg (γ + ρ).

Согласно схеме сил в винтовой паре сила трения в прямоугольной резьбе (рис. 10, а)

R_f = fN,

но при γ = 0 нормальная реакция N = F, следовательно

R_f = fF.

Для треугольной резьбы (рис. 10, б) также

R_f = fN,

где N = N′ / cos α′, α′ - угол наклона рабочей грани витка.

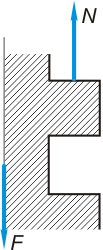
а) б)

Рис. 10. Схема сил на витках: а – прямоугольной резьбы; б – треугольной резьбы.

При γ = 0 составляющая реакции N′ = F, следовательно

R_f = fF/cos α′ = f′F,

где f′ = f / cos α′ - приведенный коэффициент трения.

Приведенный угол трения

ρ′ = arctg f′ = arctg (f / cos α′).

Таким образом, для определения окружной силы с треугольной или трапецеидальной резьбой в формулу F_t = F tg (γ + ρ) необходимо подставить вместо действительного приведенный угол трения, т. е. F_t = F tg (γ + ρ′).

Момент завинчивания

При завинчивании гайки или винта (рис. 11) к ключу прикладывают момент завинчивания

Т_зав = F_pl = T + T_f,

где F_p - сила на конце ключа;

l - расчетная длина ключа;

T - момент в резьбе от окружной силы:

T = F_t d2 /2 = (F₀ d2 / 2) tg(γ + ρ′),

F₀ - сила затяжки болта;

T_f - момент трения на опорном торце гайки или головки винта.

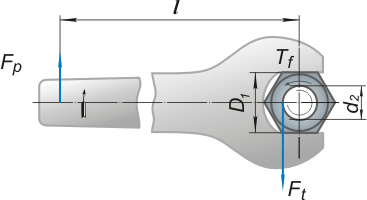
Рис. 11. Схема для определения момента завинчивания.

Опорный торец гайки представляет собой кольцо с наружным D₁ и внутренним диаметром d₀ (рис. 12). Равнодействующая сила трения R_f = R₀ f приложена на среднем радиусе R_ср = (D₁ + d₀) / 4 опорной поверхности гайки. При этом

T_f = R_f R_ср = F₀ f (D₁ + d₀) / 4.

Следовательно, момент завинчивания

Т_зав = F_p l = F₀ [(d₂ / 2) tg (γ + ρ′) + f (D₁ + d₀) / 4].

Рис. 12. Схема для определения момента трения на торце гайки.

Расчёт на прочность резьбовых соединений

Случай 1. Болт нагружен только внешней растягивающей силой F без начальной затяжки (рис. 13).

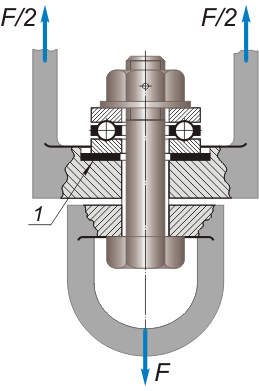
Рис. 13. Схема расчёта болта без начальной затяжки.

Опасным является сечение, ослабленное нарезкой. Расчет сводится к определению расчетного диаметра d_p резьбы из условия прочности на растяжение:

,

откуда

,

где [σ]_p - допускаемое напряжение на растяжение для болта.

Случай 2. Болтовое соединение нагружено поперечной силой F_r (рис. 14).

Рис. 14. Схема для расчёта болта, нагруженного поперечной силой.

При затяжке болта на стыке деталей возникают силы трения, которые препятствуют относительному их сдвигу. Внешняя сила F_r непосредственно на болт не передается, поэтому его рассчитывают по силе затяжки F₀:

F₀ = F_r K / (f i z)

где К - коэффициент запаса по сдвигу деталей;

f - коэффициент трения;

i - число стыков;

z - число болтов.

Расчетный диаметр резьбы болта определяют по формуле

.

Случай 3. Болтовое соединение предварительно затянутое и нагружено внешней осевой растягивающей силой (рис. 15).

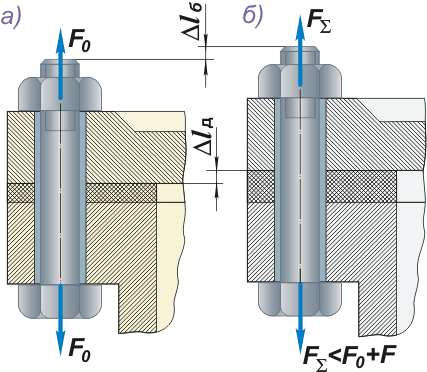
Рис. 15. Схемы для расчёта болтового соединения: а – болт затянут; б – к болту приложена сила.

Обозначим: F₀ - сила предварительной затяжки болта; F - внешняя растягивающая сила, приходящаяся на один болт.

Внешняя растягивающая сила передается болту. От этой силы болт дополнительно удлиняется на ∆l_б. На то же значение ∆l_д происходит сжатие деталей. Суммарная нагрузка на болт

F_∑ < F₀ + F.

Так как изменение нагрузки на болт со стороны сжатых деталей связано с появлением силы F, в этом случае только часть силы F (χF) воспринимается болтом, а остальная часть (1 – χ)F - сжатыми деталями. В этом случае:

F_∑ = F₀ + χ F,

где χ - коэффициент внешней нагрузки.

Лекция № 8

ШПОНОЧНЫЕ СОЕДИНЕНИЯ

8.1. Устройство, назначение и типы соединений

Шпоночные соединения служат для закрепления ни валу вращающихся деталей, а также для передачи вращающего момента от вала 1 к ступице детали 2 посредством шпонки 3 (рис. 87).

г)

д)

Рис. 87. Шпоночное соединение

Преимущества:

- надёжность конструкции;

- низкая стоимость;

- простота сборки.

Недостатки:

- ослабление вала и ступицы шпоночными пазами.

По конструкции шпонки подразделяют на:

- призматические со скруглёнными (рис. 87, а, в) и плоскими торцами (рис. 88, б);

- сегментные (рис. 87, г);

- клиновые (рис. 87, д).

8.2. Расчёт шпоночных соединений

Расчёт шпоночных соединений призматическими шпонками

Соединения призматическими шпонками проверяют на смятие.

Рис. 89. Схема к расчёту соединения призматической шпонкой.

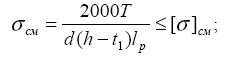
где l_p = l – b – рабочая длина шпонки со скруглёнными торцами,

l – длина шпонки.

Расчёты напряжённых шпоночных соединений клиновыми шпонками

где f – коэффициент трения на рабочих поверхностях.

Соединение фрикционной шпонкой

.

Соединение цилиндрической шпонкой

.

ШЛИЦЕВЫЕ СОЕДИНЕНИЯ

8.1. Устройство, назначение, достоинства, недостатки

Шлицевое соединение можно рассматривать как многошпоночное соединение (рис. 1).

Рис. 1. Шлицевое соединение.

Достоинства:

- высокая надёжность,

- технологичность.

Недостатки:

- высокая стоимость.

В зависимости от профиля зубьев различают три основных типа соединений (рис. 2): с прямобочными, эвольвентными и треугольными зубьями.

а) б) в)

Рис. 2. Профили зубьев: а – прямобочные; б – эвольвентные; в – треугольные.

8.2. Расчёт шлицевых соединений

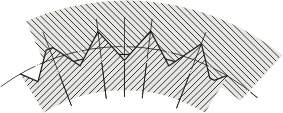
В зависимости от диаметра вала d (рис. 93) выбирают параметры зубчатого соединения, после чего соединение проверяют на смятие.

Рис. 93. Схема к расчёту шлицевого соединения прямобочными шлицами.

Для соединений с прямобочными шлицами

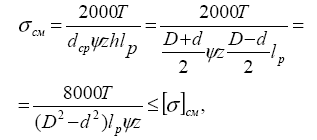
где ψ = 0,75;

z – число шлицев;

l_p – рабочая длина шлицев.

Для соединений с эвольвентным профилем зубьев

где m – модуль соединения.

СОЕДИНЕНИЯ СВАРКОЙ

8.1. Преимущества и недостатки

Существуют следующие способы сварки: ручная дуговая сварка, автоматическая дуговая сварка под слоем флюса, электрошлаковая и контактная сварка.

В зависимости от взаимного размещения соединяемых деталей различают следующие основные виды сварных соединений: стыковые, нахлёсточные, тавровые и угловые.

Достоинства:

- герметичность;

- технологичность;

- высокая производительность.

Недостатки:

- появление температурных напряжений и связанная с ними возможность искривление деталей после сварки;

- значительная концентрация напряжений возле сварных швов.

Швы стыковых соединений имеют следующие виды: односторонний без скоса кромок, односторонний со скосом кромок, двусторонний с двумя симметричными скосами одной кромки, двусторонний с двумя симметричными скосами двух кромок (рис. 1).

Рис. 1. Стыковые швы: а - односторонний без скоса кромок; б - односторонний со скосом кромок; в - двусторонний с двумя симметричными скосами одной кромки; г - двусторонний с двумя симметричными скосами двух кромок.

Швы, предназначенные для соединения элементов, расположенных в разных (параллельных или пересекающихся плоскостях), называются угловыми. В зависимости от формы сечения различают швы в виде равнобедренного треугольника; треугольника, основание которого больше высоты; треугольника с криволинейными сторонами (рис. 2). За катет шва принимают меньший катет вписанного в сечение шва треугольника. Катет шва выбирают из условия k ≤ s.

Рис. 2. Угловые швы: нормальная (а), вогнутая (б), выпуклая (в) и специальная (г) форма сечения.

В зависимости от размещения шва относительно линии действия силы F угловые швы называют лобовыми, фланговыми, и комбинированными (рис. 3).

Рис. 3. Нахлесточные соединения угловыми швами: а - лобовой шов; б - фланговый шов; в - комбинированный шов