Тема 3: элементы векторного анализа.

Сложение, вычитание векторов, угол между векторами, скалярное произведение векторов.

Проверка на базис.

Линейный оператор. Собственные значения и собственные векторы линейных операторов.

Квадратичная форма. Исследование на знакоопределенность квадратичной формы.

1. СЛОЖЕНИЕ, ВЫЧИТАНИЕ ВЕКТОРОВ, УГОЛ МЕЖДУ ВЕКТОРАМИ, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец с концом вектора при условии, что начало вектора совпадает с концом вектора (рис 1) (правило треугольников).

Очевидно, что вектор в этом случае представляет диагональ параллелограмма, построенного на векторах и (рис 1) (правило параллелограмма).

Рис. 1.

Разностью двух векторов и называется сумма вектора и вектора , противоположного . Легко убедится в том, что на параллелограмме, построенном на векторах и это будет другая диагональ (рис 2).

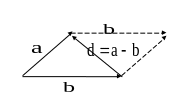
Рис. 2.

Координатами вектора называются координаты его конечной точки.

Если и , то суммой и разностью являются соответственно векторы:

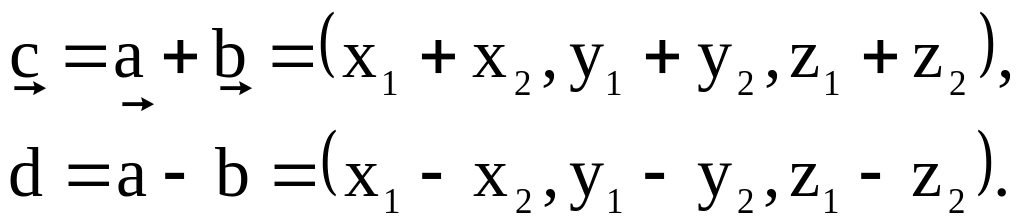
А произведение вектора на число есть вектор .

Длина вектора равна корню квадратному его из суммы квадратов его координат:

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними:

Угол между векторами и определяется по формуле

Пример 3.1. Даны векторы:

Найти:

а) векторы и ;

б) длины векторов и ;

в) скалярный квадрат вектора ;

г) скалярное произведение векторов ;

д) угол меду векторами и ;

Решение:

а) По определению и .

б) Найдем длины векторов:

в) Скалярный квадрат вектора равен квадрату модуля вектора, т.е.:

г) Найдем скалярное произведение:

д) Найдем угол между векторами:

откуда

2. ПРОВЕРКА НА БАЗИС.

Совокупность линейно независимых векторов мерного пространства называются базисом.

Векторы векторного пространства называются линейно зависимыми, если существуют такие числа , такие что хотя бы одно из них отлично от нуля, и выполняется равенство:

.

Если три вектора являются линейно независимыми (т.е. являются базисом) то они компланарны (не лежат в одной плоскости или на параллельных плоскостях).

Необходимым и достаточным условием компланарности трех векторов, заданных в декартовом базисе, является равенство нулю определителя третьего порядка, в первой строке которого записаны координаты первого вектора, во второй строке – второго, в третьей – третьего.

Пример 3.2. Проверить, образуют ли вектора базис.

и найти координаты вектора в этом базисе.

Решение.

Базис в трехмерном пространстве могут образовывать любые три линейно независимые вектора, для этого построим определитель, и убедимся что он не равен нулю.

Итак, векторы образуют базис. По теореме про линейную зависимость любых четырех векторов в трехмерном пространстве разложим вектор на векторах .

где искомые координаты вектора .

Решая полученную систему уравнений получим . Таким образом вектор имеет в базисе такие координаты .

3. ЛИНЕЙНЫЙ ОПЕРАТОР

Если задан закон (правило), по которому каждому вектору пространства ставится в соответствие единственный вектор пространства , то говорят, что задан оператор , действующий из в , и записывают .

Оператор называется линейным, если для любых векторов и пространства и любого числа выполняются соотношения:

1. - свойство аддитивности оператора;

2. - свойство однородности оператора.

Вектор называется образом вектора , а сам вектор - прообразом вектора .

Каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице -ого порядка соответствует линейный оператор -мерного пространства.

Связь между вектором и его образом можно выразить в матричной форме уравнением:

,

где А – матрица линейного оператора, , - матрицы-столбцы из координат векторов и .

Пример 3.3. Пусть в пространстве линейный оператор в базисе задан матрицей . Найти образ вектора .

Решение.

По формуле имеем:

Следовательно, .

4. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ

Вектор называется собственным вектором линейного оператора , если найдется такое число , что

.

Число называется собственным значением оператора (матрицы А), соответствующим вектору .

Равенство можно переписать в матричной форме:

отсюда получим:

.

Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения системы необходимо и достаточно, чтобы определитель системы был равен нулю.

Определитель является многочленом -ой степени относительно . Этот многочлен называется характеристическим многочленом оператора или матрицы А, а уравнение характеристическим уравнением оператора или матрицы А.

Пример 3.4. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей .

Решение. Составляем характеристическое уравнение или ,

откуда собственные значения линейного оператора .

Находим собственный вектор , соответствующий собственному значению . Для этого решаем матричное уравнение:

, или .

Откуда находим или . Положив , получим, что векторы при являются собственными векторами линейного оператора с собственным значением .

Аналогично определяем вектор при любом являются собственными векторами линейного оператора с собственным значением .

5. ИССЛЕДОВАНИЕ НА ЗНАКООПРЕДЕЛЕННОСТИ КВАДРАТИЧНОЙ ФОРМЫ

Квадратичной формой от переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух переменных, взятых с некоторым коэффициентом:

.

Предполагается, что коэффициенты квадратичной формы - действительные числа, причем . Матрица , составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид:

где - матрица-столбец переменных.

Теорема. Для того чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения матрицы А были положительны (отрицательны).

Если собственные значения разных знаков то знакоопределённость квадратичной формы установить нельзя.

В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.

Теорема. Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. , где:

, , …,

Для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка:

, , …, .

Если не один из критериев не выполняется, то знакоопределённость матрицы не устанавливается.

Пример 3.5. Проверить знакоопределенность квадратичной формы

a)

б)

Решение:

а) При помощи собственных значений:

Матрица квадратичной формы имеет вид . Для матрицы А характеристическое уравнение имеет вид:

или .

Решая уравнение найдем . Так как корни характеристического уравнения матрицы А положительны, но квадратичная форма положительно определенная.

При помощи критерия Сильвестра:

Так как главные миноры матрицы А

положительны, то по критерию Сильвестра данная квадратичная форма положительно определенная.

б) Матрица квадратичной формы имеет вид . Поскольку при нахождении собственных значений получим уравнение третей степени, для определения знакоопределенности воспользуемся для удобства лишь критерием Сильвестра.

Главные миноры матрицы А:

.

Так как знаки миноров чередуются начиная со знака «минус», то это означает что квадратичная форма отрицательно определена.