
- •Тема 1. Матрицы и определители.
- •Тема 2. Системы линейных алгебраических уравнений (слау)
- •Тема 3: элементы векторного анализа.
- •Тема 4. Пределы и непрерывность.
- •Тема 5. Производная.
- •Тема 6. Неопределенный интеграл.
- •Тема 7. Определенный интеграл.
- •Тема 8. Дифференциальные уравнения.
- •1. Однородные уравнения.
- •1) Однородные линейные уравнения с постоянными
- •Тема 9. Числовые ряды.
- •Степенные ряды. Свойства степенных рядов
- •12.5. Ряды тейлора и маклорена. Разложение функций в ряд
Тема 1. Матрицы и определители.
Умножение матриц.
Нахождение определителя.
Нахождение обратной матрицы.
Определение ранга матрицы.
УМНОЖЕНИЕ МАТРИЦ.
Для того чтобы
умножить матрицу А размерности
![]() (
(![]() - количество строк,
- количество строк,
![]() - количество столбцов) на матрицу В
размерности
- количество столбцов) на матрицу В
размерности
![]() необходимо следовать следующему
алгоритму:
необходимо следовать следующему
алгоритму:
Проверить существует ли произведение АВ, т.е. совпадает ли количество столбцов матрицы А с количеством строк матрицы В. Если совпадает, то переходим ко второму шагу, иначе произведение не существует.
Определить размерность результирующей матрицы С по следующему правилу: необходимо записать последовательно размерности сначала матрицы А, а затем размерность матрицы В, и исключить серединку, т.е.

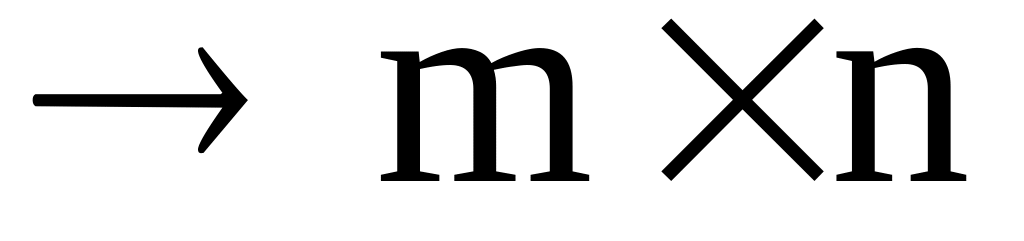 (
исключили). Таким образом размерность
матрицы С будет
строк и
(
исключили). Таким образом размерность
матрицы С будет
строк и
 столбцов.
Затем необходимо определить элементы
результирующей матрицы.
столбцов.
Затем необходимо определить элементы
результирующей матрицы.Каждый элемент
 результирующей матрицы С, размерности
результирующей матрицы С, размерности
 ,
равен сумме произведений элементов
,
равен сумме произведений элементов
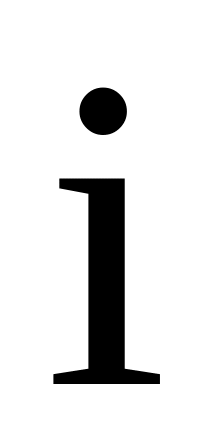 -ой
строки матрицы А на соответствующие
элементы
-ой
строки матрицы А на соответствующие
элементы
 -ого
столбца матрицы В, т.е.
-ого
столбца матрицы В, т.е.
![]()
![]() ;
;
![]() .
.
Пример 1.1. Даны матрицы А и В. Найти АВ и ВА.
![]()

Решение:
Для решения воспользуемся описанным выше алгоритмом.
Произведение АВ существует так как количество столбцов матрицы А (3 столбца) совпадает с количеством строк матрицы В (3 строки). Также существует и произведение ВА (2 столбца и 2 строки).
Определим размерность матриц С и
 ,
которые получаются в результате
произведения матриц АВ и ВА соответственно.
,
которые получаются в результате
произведения матриц АВ и ВА соответственно.
Размерность
матрицы
![]() :
: ![]()
![]()
![]()
Размерность
матрицы
![]() :
:
![]()
Таким образом матрица С содержит 2 строки и 2 столбца, матрица содержит 3 строки и 3 столбца.
Определим элементы матрицы С и :
![]()
![]()


Умножение матриц в Microsoft Excel.
Для умножения матриц используется стандартная функция МУМНОЖ.
Функция возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.
МУМНОЖ(массив1;массив2)
Массив1, массив2 — перемножаемые массивы(матрицы).
Замечание. Количество столбцов аргумента массив1 должно быть таким же, как количество сток аргумента массив2, и оба массива должны содержать только числа.
Решение примера 1.1 в Microsoft Excel:
Запускаем Microsoft Excel.
Вводим матрицы в виде массивов чисел. Матрица А записывается в диапазоне ячеек А2:С3. Матрица В записывается в диапазоне ячеек А5:В7.
Поскольку матрица А содержит 3 столбца а матрица В содержит 3 строки, то произведение АВ существует. Результатом умножения матрицы А на матрицу В будет матрица С, размерности 2х2, т.е.
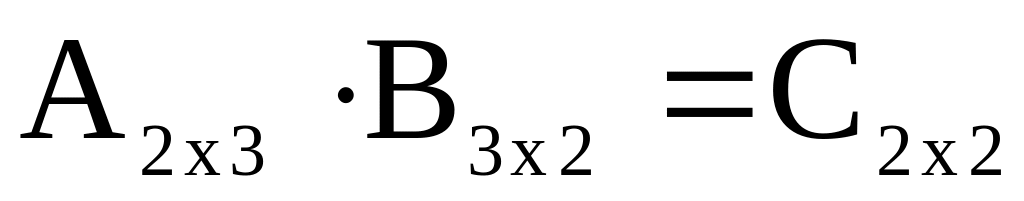 .
Поэтому подготовим диапазон ячеек куда
будет выведен массив чисел матрицы С,
для этого выделим ячейки В9:С10.
.
Поэтому подготовим диапазон ячеек куда
будет выведен массив чисел матрицы С,
для этого выделим ячейки В9:С10.В меню Вставка>Функция выбираем функцию МУМНОЖ (она находится в математических функциях). Вводим в поле массив1 диапазон ячеек А2:С3 а в поле массив2 диапазон А5:В7. Нажимаем ОК, затем для корректного вывода массива чисел нажимаем клавишу F2, а затем сочетание клавиши CTRL+SHIFT+ENTER.
В результате выполненных операций диапазон ячеек В9:С10 будут записаны элементы матрицы .
Аналогично найдём произведение ВА.
Поскольку матрица В содержит 2 столбца а матрица А содержит 2 строки, то произведение АВ существует. Результатом умножения матрицы В на матрицу А будет матрица D, размерности 3х3, т.е.
 .
Поэтому подготовим диапазон ячеек куда
будет выведен массив чисел матрицы D,
для этого выделим ячейки B12:D14.
.
Поэтому подготовим диапазон ячеек куда
будет выведен массив чисел матрицы D,
для этого выделим ячейки B12:D14.В меню Вставка>Функция выбираем функцию МУМНОЖ. Вводим в поле массив1 диапазон ячеек А5:В7 а в поле массив2 диапазон А2:С3. Нажимаем ОК, затем для корректного вывода массива чисел нажимаем клавишу F2, а затем сочетание клавиши CTRL+SHIFT+ENTER.
В результате выполненных операций диапазон ячеек B12:D14 будут записаны элементы матрицы .
2. НАХОЖДЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ.
Определителем
матрицы первого порядка
![]() ,
или определителем первого порядка,
называется элемент
,
или определителем первого порядка,
называется элемент
![]() :
:
![]() .
.
Определителем
квадратной матрицы второго порядка
![]() ,
или определителем второго порядка,
называется число, которое вычисляется
по формуле:
,
или определителем второго порядка,
называется число, которое вычисляется
по формуле:
![]() .
.
Пусть дана квадратная матрица третьего порядка:
 .
.
Определителем матрицы третьего порядка А, или определителем третьего порядка, называется число, которое вычисляется по формуле:
![]() .
.
Определители квадратных матриц более высоких порядков определяются по теореме Лапласа.
Пример 1.2. Даны
матрицы
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
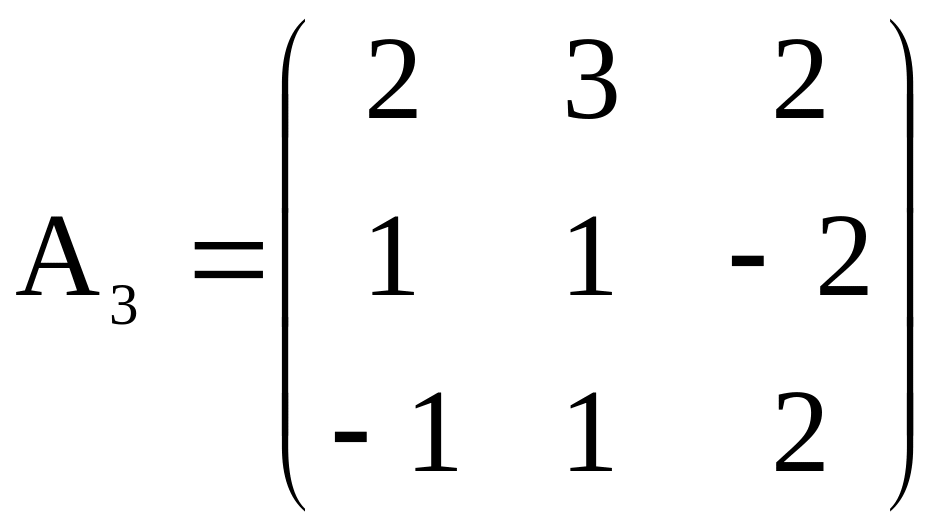
Найти
![]() -?
-?
Решение:
![]()
![]()
![]()
Нахождение определителя матрицы в Microsoft Excel.
Для нахождения определителя матрицы используется стандартная функция МОПРЕД.
Функция возвращает определитель матрицы (матрица хранится в массиве).
МОПРЕД(массив)
Массив — числовой массив с равным количеством строк и столбцов.
Решение примера 1.2. в Microsoft Excel:
Найдем определитель матрицы .
Запускаем Microsoft Excel, если запущен, то переходим на новый лист.
Вводим матрицу А в диапазон ячеек А2:С4.
Выделяем свободную ячейку В6 куда будет выведен результат.
В меню Вставка>Функция выбираем функцию МОПРЕД. Вводим в поле массив диапазон ячеек А2:С4. Нажимаем ОК.
В результате выполненных операций в ячейке В6 будет записано значение определителя матрицы
 .
.
НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ.
Матрица
![]() называется обратной по отношению к
квадратной матрице А, если при умножении
этой матрицы на данную как справа, так
и слева получается единичная матрица:
называется обратной по отношению к
квадратной матрице А, если при умножении
этой матрицы на данную как справа, так
и слева получается единичная матрица:
![]() .
.
Алгоритм вычисления обратной матрицы:
Находим определитель исходной матрицы. Если
 ,
то матрица А – вырожденная и обратной
матрицы
не существует. Если
,
то матрица А – вырожденная и обратной
матрицы
не существует. Если
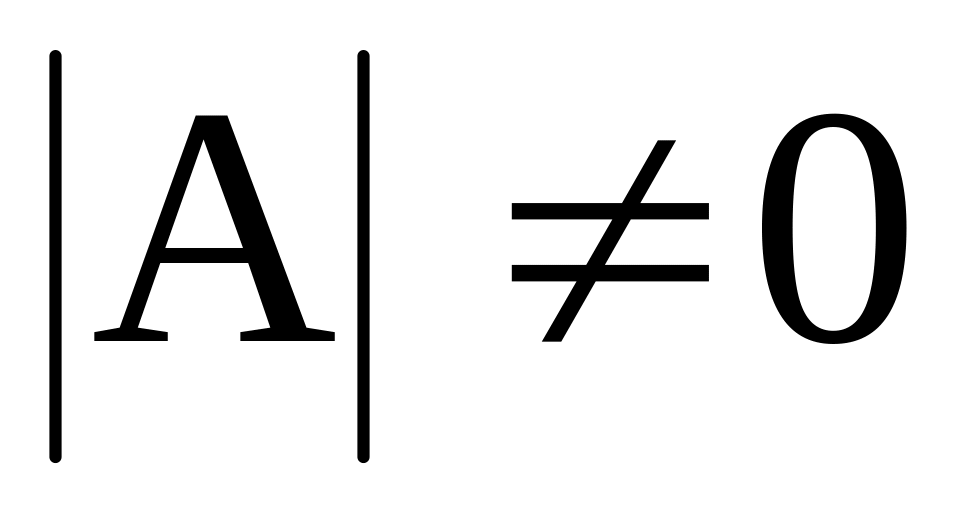 ,
то матрица А – невырожденная и обратная
матрица существует.
,
то матрица А – невырожденная и обратная
матрица существует.Находим матрицу
 ,
транспонированную к А.
,
транспонированную к А.Находим алгебраические дополнения элементов транспонированной матрицы
 и составляем из них присоединенную
матрицу
и составляем из них присоединенную
матрицу
 .
.Вычисляем обратную матрицу по формуле:
![]() .
.
Проверяем правильность вычисления обратной матрицы , исходя из ее определения (пункт 5 не обязателен).
Пример 1.3. Найти матрицу, обратную к данной:

Решение:
Для нахождения обратной матрицы воспользуемся описанным выше алгоритмом.
Определитель матрицы
 (см.
пример 2), т.е. матрица А – невырожденная
и обратная матрица
существует.
(см.
пример 2), т.е. матрица А – невырожденная
и обратная матрица
существует.Находим матрицу , транспонированную к А:

Находим алгебраические дополнения элементов матрицы и составляем из них присоединенную матрицу
 :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 .
.
Вычисляем обратную матрицу :

Нахождение обратной матрицы в Microsoft Excel.
Для нахождения обратной матрицы используется стандартная функция МОБР.
Функция возвращает обратную матрицу для матрицы, хранящейся в массиве.
МОБР(массив)
Массив — числовой массив с равным количеством строк и столбцов.
Решение примера 1.3. в Microsoft Excel:
Запускаем Microsoft Excel, если запущен, то переходим на новый лист.
Вводим матрицу А в диапазон ячеек А2:С4.
Выделяем свободные ячейки А6:С8 куда будет выведен результат.
В меню Вставка>Функция выбираем функцию МОБР. Вводим в поле массив диапазон ячеек А2:С4. Нажимаем ОК, затем для корректного вывода массива чисел нажимаем клавишу F2, а затем сочетание клавиши CTRL+SHIFT+ENTER.
В результате выполненных операций в ячейках А2:С4 будет записана обратная матрица
 .
.
ОПРЕДЕЛЕНИЕ РАНГА МАТРИЦЫ
В матрице А размера
вычеркиванием каких-либо строк и столбцов
можно вычленить квадратные подматрицы
-ого
порядка, где
![]() .
Определители таких подматриц называются
минорами
-ого
порядка матрицы А.
.
Определители таких подматриц называются
минорами
-ого
порядка матрицы А.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Из определения следует:
а) ранг матрицы
![]() не превосходит меньшего из ее размеров,
т.е.
не превосходит меньшего из ее размеров,
т.е.
![]() 4
4
б)
![]() тогда и только тогда, когда все элементы
матрицы равны нулю, т.е. А = 0;
тогда и только тогда, когда все элементы
матрицы равны нулю, т.е. А = 0;
в) для квадратной
матрицы
-ого
порядка
![]() тогда и только тогда, когда матрица А –
невырожденная.
тогда и только тогда, когда матрица А –
невырожденная.
Теорема. Ранг матрицы не изменяется при элементарных преобразования матрицы.
К элементарным преобразованиям матрицы относятся следующие:
1) Отбрасывание нулевой строки (столбца).
2) Умножение всех элементов сроки (столбца) матрицы на число, не равное нулю.
3) Изменение порядка строк (столбцов) матрицы.
4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженного на любое число.
5) Транспонирование матрицы.
С помощью элементарных преобразований можно матрицу к ступенчатому виду (когда все элементы расположенные выше (ниже) главной диагонали равны нулю), когда вычисление ее ранга не представляет труда.
Рассмотрим алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример 4.
Найти ранг матрицы:

Решение:
Если
 ,
то при перестановке строк или столбцов
добиваемся того, что
,
то при перестановке строк или столбцов
добиваемся того, что
 .
В данном примере поменяем местами,
например, 1-ю и 2-ю строки матрицы:
.
В данном примере поменяем местами,
например, 1-ю и 2-ю строки матрицы:

Если , то умножая элементы 2-й, 3-й и 4-й строк на подходящие числа (именно на
 ,
,
 ,
,
 )
и прибавляя полученные числа соответственно
к элементам 2-й, 3-й и 4-й строк, добьемся
того, чтобы все элементы 1-го столбца
(кроме
)
равнялись нулю:
)
и прибавляя полученные числа соответственно
к элементам 2-й, 3-й и 4-й строк, добьемся
того, чтобы все элементы 1-го столбца
(кроме
)
равнялись нулю:

Если в полученной матрице
 (у нас
(у нас
 ),
то умножая элементы 3-й и 4-й строк на
подходящие числа (а именно, на
),
то умножая элементы 3-й и 4-й строк на
подходящие числа (а именно, на
 ,
,
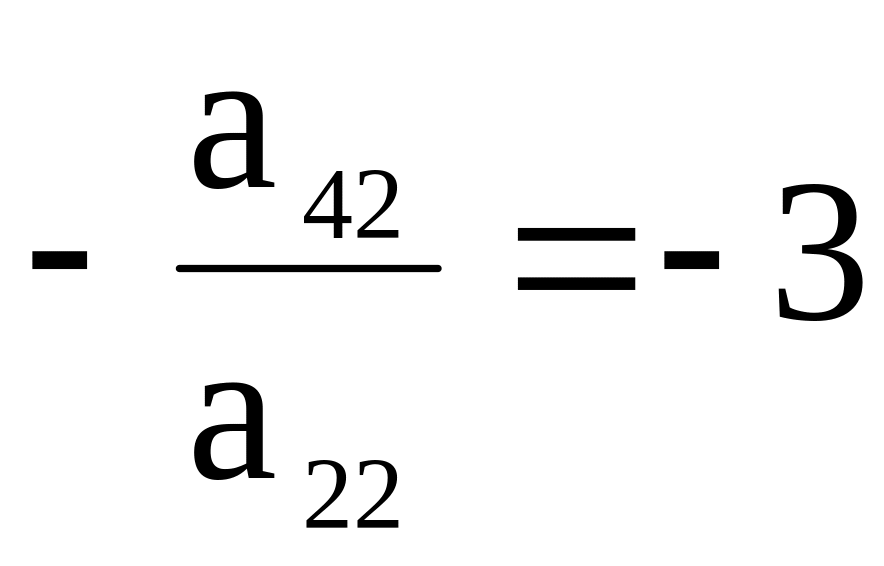 ),
добьемся того, чтобы все элементы 2-го
столбца (кроме
),
добьемся того, чтобы все элементы 2-го
столбца (кроме

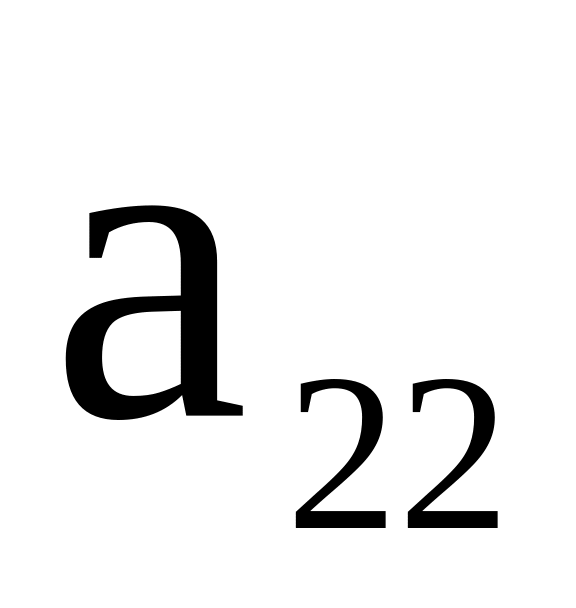 )
равнялись нулю. Если в процессе
преобразований получаются строки (или
столбцы), целиком состоящие из нулей
(как в данном примере), то отбрасываем
эти строки (или столбцы):
)
равнялись нулю. Если в процессе
преобразований получаются строки (или
столбцы), целиком состоящие из нулей
(как в данном примере), то отбрасываем
эти строки (или столбцы):

Последняя матрица
имеет ступенчатый вид и содержит миноры
второго порядка, не равные нулю, например,
![]() .
Поэтому ранг полученной ступенчатой,
а следовательно, и данной матрицы равен
2.
.
Поэтому ранг полученной ступенчатой,
а следовательно, и данной матрицы равен
2.
