2.4 Расчет листа «РегенСис».

Математическое описание и аналитическое решение уравнений элементов тепловой схемы выполняем последовательно против хода питательной воды (на­чиная от верхнего ПВД).

Математическое описание группы пвд

1. Уравнение теплового баланса ПВД 7 и его решение относительно расхода греющего пара:

, (15)

тогда

, (16)

где – расход и энтальпия пара от концевого уплотнения ЦВД в ПНД 7;

- расход сливаемого дренажа из ПНД 7. (17)

2. Уравнение теплового баланса ПВД 6 и его решение относительно расхода греющего пара:

, (18)

значит:

, (19)

где (20)

3. Уравнение теплового баланса ПВД 5 и его решение относительно расхода греющего пара:

, (21)

, (22)

где – энтальпия питательной воды на выходе из питательного насоса,

(23)

Используемые обозначения:

– расход греющего пара, поступающего в i-й подогреватель;

– энтальпия греющего пара из j-й камеры регенеративных отборов;

– расход питательной воды;

– энтальпия питательной воды на выходе i-го подогревателя;

– расход сливаемого дренажа из i-ого подогревателя

– коэффициент, учитывающий рассеивание теплоты от i-го подогревателя в окружающую среду.

1. Математическое описание деаэратора

Деаэратор моделируется уравнениями материального и теплового баланса.

1. Уравнение материального баланса (УМБ) деаэратора

, (24)

где – расходы пара из деаэратора на концевые уплотнения турбины и на эжекторы; – расход пара от уплотнений штоков клапанов в деаэратор.

2. Уравнение теплового баланса (УТБ) деаэратора

, (25)

где – коэффициент рассеивания теплоты деаэратора;

– энтальпия питательной воды на выходе из деаэратора;

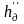– энтальпия насыщенного пара, уходящего из деаэратора на уплотнения и эжекторы;

– энтальпия свежего пара.

В УМБ деаэратора две неизвестные переменные:

– расход основного конденсата на выходе ПНД 4,

– расход греющего пара в деаэратор.

Выражая из УМБ деаэратора и подставляя его в УТБ, определяем :

(26)

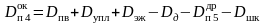(27)

Математическое описание пнд и псг

1. Уравнение теплового баланса ПНД 4 и его решение относительно расхода греющего пара:

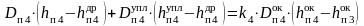, (28)

откуда

, (29)

где – расход и энтальпия смешанного потока пара, поступающего в ПНД 4 от камер концевых уплотнений;

Расход сливаемого из ПНД 4 дренажа составляет . (30)

2. Уравнение теплового баланса ПНД 3 и его решение относительно расхода греющего пара:

, (31)

, (32)

где энтальпию на входе в ПНД-3 принимаем в качестве итеративной пере­менной;

- расходы основного конденсата в ПНД 3 и ПНД 4 равны;

Расход сливаемого конденсата (дренажа) из ПНД 3,используемое для дальнейшего расчета, равен:

. (33)

3. Уравнения материального и теплового баланса смесителя С2:

, (34)

, (35)

где энтальпия основного конденсата на выходе из смесителя С2;

и расход и энтальпия в точке смешения сливов основного конденсата из ПНД2 и ПСГ2(формулы для их определения приведены ниже).

Используя уравнение (35) теплового баланса для С2, получаем выражение для итеративного уточнения значения энтальпии основного конденсата на входе в ПНД 3:

. (36)

Следующая итерация не выполняется если кДж/кг. (37)

4. Запишем систему из 3-х уравнений:

₍₃₈₎

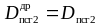
Первое уравнение этой системы - тепловой баланс для ПСГ2, а второе – материальный баланс в точке С2.

Расход , необходимый для определения неизвестен.

Запишем систему уравнений для верхнего сетевого подогревателя ПСГ2:

, (39)

откуда выражаем :

, (40)

где и энтальпия воды на выходе из ПСГ 1 и ПСГ 2 соответственно, определенные как и ранее на листе “Теплофикационная установка”.

Из 1-ого и 2-ого уравнений системы (38) получаем выражение для расхода пара В ПНД 2:

(41)

Эта формула вычисляется при итеративном задании значения . Значение итеративной переменной уточняется после расчета подсистемы состоящей из ПНД 1, ПСГ 1 и С1.Теперь расчитываем из 2-ого уравнения системы _.

_{Далее составив тепловой и материальный баланс для точки смешения сливов из ПГС2 и ПНД2 выразим} и _:

(42)

_{,где . Значение рассчитано в ячейке Q35 листа} «РегенСис».

5. Система из 3–х уравнений для ПНД 1, ПСГ 1:

,

, (43)

,

где 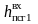- равна энтальпии обратной сетевой воды, определенной ранее;

= - энтальпия на входе в ПНД 1 значение которой пока неизвестно. Присваиваем ей начальное значение равное максимально допустимому на выходе из сальникового подогревателя, равное 248 кДж/кг. Из последнего уравнения системы (43) выражаем который равен :

(44)

Заметим, что = .

После определяе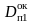м , а затем из 1-ого и 2-ого уравнений системы (43).

Для итеративного уточнения значения переменной используется УТБ смесителя С1, решенное относительно энтальпии выходящего потока

(45)

Итеративный расчет по методу поиск решения заканчивается если

кДж/кг. (46)

Также в дальнейшем необходимо соблюдение кДж/кг. (47)

присваиваем равным .

Расчет контура рециркуляции

Энтальпия потока после сальникового подогревателя:

(48)

Задавались расходом основного конденсата в КН , контролируя при этом значение энтальпии конденсата, проходящей через клапан рециркуляции.

кДЖ/кг.

Расход по линии рециркуляции:

₍₄₉₎

=39 кг/с, исходя из диаметра трубопровода рециркуляции. (В моем расчете данное условие не было выполнено в связи с высоким давлением в конденсаторе Pк=0,005 МПа)

=39 кг/с, по условиям работы ЭУ.