3.4. Структурные методы автоматической коррекции погрешностей средств измерительной техники

Выбор той или иной структурной схемы инвариантных СИТ с автоматической коррекцией погрешностей определяется видом измеряемой величины, нужной точностью измерений, простотой аппаратурной реализации и другими факторами. В зависимости от наличия связи выхода со входом СИТ их структурные схемы могут быть разомкнутыми и замкнутыми.

Корректирующее влияние при структурной коррекции погрешностей СИТ может образовываться с помощью или дополнительного измерительного канала (пространственное разделение), или дополнительного цикла измерения (временное разделение).

Как при пространственном, так и при временном разделении каналов корректирующее влияние может вводиться в основной измерительный канал адитивно, мультипликативно и комбинировано. Рассмотрим типичные структурные схемы инвариантных СИТ с пространственным и временным разделением измерительных каналов.

3.4.1. Разомкнутые структурные схемы инвариантных средств измерительной техники

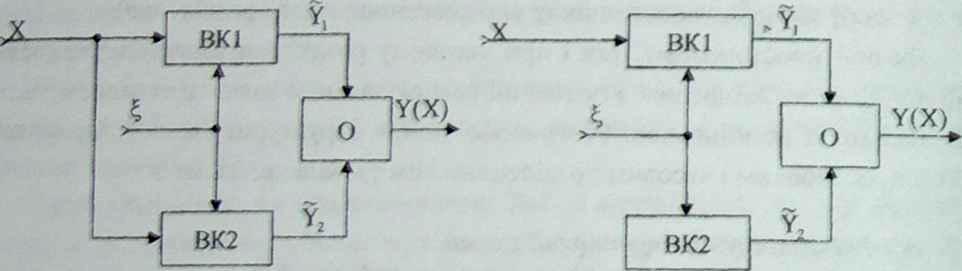
Два варианта обобщенных разомкнутых структурных схем инвариантных СИТ с пространственным разделением каналов приведены на рис.3.4. Они имеют одинаковый состав функциональных блоков - по два измерительных канала (ИК1 и ИК2) и вычислитель (В), но отличаются алгоритмом обработки выходных величин измерительных каналов Y₁ и Y₂.

В схеме (рис.3.4,а) измеряемая величина X подается на оба канала (ИК1 и ИК2), а в схеме (рис.3.4,б) - на один канал (ИК1). Влияющая величина  согласно с принципом инвариантности в обеих схемах поступает на оба измерительных канала. Выходные величины и ИК1 и ИК2 соответственно подаются в вычислитель В, где исключают зависимость выходной величины вычислителя Y(Х) от влияющей величины .

Запишем функции преобразования измерительной информации в обеих схемах СИТ.

Для СИТ со структурной схемой (рис.3.4,а) имеем:

- для величины Y₁ на выходе ИК1

= f₁(X,);

-для величины на выходе ИК2

= f₂(X,);

- для величины Y на выходе вычислителя

Y = f( , ) = Y(Х).

Аналогично для СИТ со структурной схемой (рис.3.4,б) запишем:

= f₁(X,);

= f₂(X,);

Y = f( , ) = Y(Х).

Рис.3.4. Разомкнутые структурные схемы инвариантных СИТ с пространственным разделением каналов, в которых измеряемая величина X направляется: а - на оба измерительных канала (ИК1 и ИК2); б - на один измерительный канал (ИК1)

Если влияющих величин несколько (₁ ,,…), то количество измерительных каналов инвариантного СИТ зависит от измеряемой величины X, количества влияющих величин и связей между каналами. Структурные схемы таких СИТ могут строиться аналогично схемам на рис.3.4, а также как комбинация этих схем.

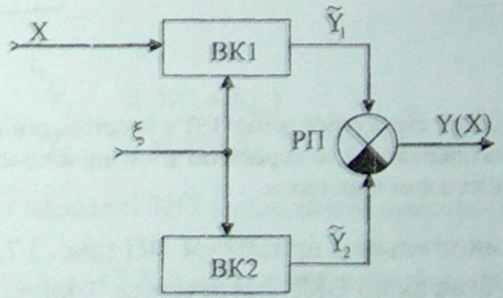
Разомкнутая схема инвариантного СИТ с временным разделением каналов, или циклическим по времени введением измерительной информации в вычислитель приведена на рис.3.5.

В этой схеме выделен третий измерительный канал ИК3, который объединяет общие элементы схемы СИТ, и введен переключатель S. Измерение выполняется за два цикла: первый цикл - переключатель S в состоянии I, второй цикл - переключатель S в состоянии II. Алгоритм обработки измерительной информации в вычислителе является аналогичным алгоритму для схемы (рис.3.4.б).

Рис.3.5. Разомкнутая структурная схема СИТ с временным разделением каналов

Выделение ИК3 позволяет уменьшить, во-первых, погрешность от неидентичности измерительных каналов ИК1 и ИК2 и, во-вторых, количество элементов в схеме СИТ.

Если влияющая величина  имеет только аддитивний характер или только мультипликативний характер, то остается справедливой структурная схема СИТ на рис.3.4,а, но в ней конкретизируется вычислитель В. Так, для исключения аддитивного влияния  (аддитивная коррекция) как вычислитель используется разностное устройство(рис.3.6)

Рис. 3.6. Разомкнутая структурная схема СИТ с пространственным разделением каналов и аддитивной коррекцией

Для статического режима измерений согласно формуле (3.1) запишем соотношение для выходных величин и измерительных каналов ИК1 и ИК2:

= k₁Х + k_1 = k₁Х + _1ад ; (3.10)

= k_2 = _2ад , (3.11)

где k₁, k_1 - соответственно коэффициенты передачи измерительного канала ИК1 для измеряемой величины X и влияющей величины ;

_1ад = k_1; _2ад = k_2 - соответственно аддитивные погрешности измерительных каналов ИК1 и ИК2, обусловленные влияющей величиной .

Как видно из уравнений (3.10) и (3.11), СИТ будет инвариантным к влияющей величине при условии _1ад = _2ад или k_1 = k_2, что отвечает выходной величине разностного устройства

Y(Х) = - = k₁Х + _1ад - _2ад = k₁Х,

которая действительно не зависит от влияющей величины .

Для исключения мультипликативного влияния  (мультипликативная коррекция) как вычислитель может использоваться или множительное устройство (МП), или делительное устройство (ДП) (рис.3.7). В обеих схемах измеряемая величина X поступает на измерительный канал ИК1, а на измерительный канал ИК2 подается образцовая величина Х₀. Ее называют калибровочной величиной, а операцию - мультипликативной коррекцией погрешности СИТ.

Рис.3.7. Разомкнутые структурные схемы СИТ с пространственным разделением каналов и мультипликативной коррекцией: а - с множительным устройством; б - с делительным устройством

Схема СИТ с множительным устройством МП (рис.3.7,б) выполняется так, что влияющая величина , на входе ИК2 инвертируется. Тогда для выходных величин и измерительных каналов ИК1 и ИК2, согласно формуле (3.3), имеем:

= k₁Х(1 + k_1) = k₁Х(1 + _1м);

= k₂Х₀(1 – k_2) = k₂Х₀(1 - _2м),

где k₁, k₂ - номинальные коэффициенты передачи измерительных каналов ИК1 и ИК2 по измеряемой величине X;

k_1, k_2 - коэффициенты передачи измерительных каналов ИК1 и ИК2 по влияющей величине ;

_1м = k_1, _2м = k_2 - относительные мультипликативные погрешности измерительных каналов ИК1 и ИК2 соответственно.

Выходная величина Y(Х) на выходе множительного устройства равняется

Y(Х) = = k₁k₂Х₀Х(1 + _1м)(1 - _2м),

или, пренебрегая величиной второго порядка малости _1м, _2м получим

Y(Х) = k₁k₂Х₀Х(1 + _1м - _2м),

При условии равенства относительных мультипликативных погрешностей _1м = _2м, или коэффициентов передачи влияющей величины k_1 = k_2 , это выражение принимает вид

Y(Х) = k₁k₂Х₀Х = kХ,

где k = k₁k₂Х₀ - коэффициент передачи СИТ с множительным устройством. Как видно из формулы (3.12), выходная величина Y(Х) СИТ с множительным устройством не зависит от мультипликативной влияющей величины .

Схема СИТ с делительным устройством ДП (рис.3.7,б) выполняется так, что влияющая величина  проходит через измерительные каналы ИК1 и ИК2 с одинаковым знаком, тогда для выходных сигналов и этих каналов запишем:

= k₁Х(1 + _1м);

= k₂Х₀(1 + _2м).

Тогда выходная величина Y(Х) на выходе делительного устройства ДП (и СИТ) при условии _1м = _2м

, (3.13)

где k = k₁ / (k₂Х₀) - коэффициент передачи СИТ с делительным устройством.

Следовательно, согласно формуле (3.13), результат измерения Y(Х) СИТ с делительным устройством не зависит от мультипликативной величины .

В тех случаях, когда влияющая величина приводит к погрешности СИТ, которая содержит аддитивную и мультипликативную составляющие, необходимо использовать комбинацию двух предыдущих схем.