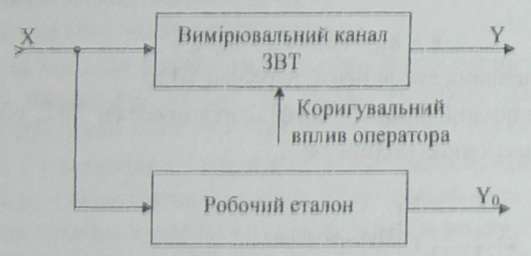
3.3. Коррекция погрешностей средств измерительной техники при участии оператора

Эта коррекция может осуществляться с ручным влиянием и без влияния оператора на СИТ.

3.3.1. Коррекция погрешностей средств измерительной техники с помощью ручного влияния оператора

Ручная коррекция погрешностей СИТ разделяется на аддитивную и мультипликативную.

Аддитивная коррекция (или установка нуля) направлена на исключение аддитивной погрешности СИТ. Она осуществляется регулировкой «Установка 0», которой градуировочная характеристика СИТ смещается параллельно самой себе. В стрелочных измерительных приборах такая регулировка выполняется оператором посредством смещения указания прибора на нулевую отметку при нулевом значении измеряемой величины (X = 0).

Мультипликативная коррекция (или калибровка) направлена на исключение мультипликативной погрешности СИТ. Она осуществляется изменением его чувствительности, то есть изменением крутизны (угла наклона) градуировочной характеристики СИТ, которая выполняется ручной регулировкой «Калибровка». При этом в схемах коррекции мультипликативной погрешности СИТ могут использоваться меры, образцовые измерительные приборы и образцовые обратные преобразователи с разностным устройством. Наиболее распространенными являются схемы коррекции с мерой (рис.3.1), которая может быть внутренней или внешней.

При наличии мультипликативной погрешности в режиме измерения величины X (состояние I переключателя S) сигнал измерительной информации Y на выходе измерительного канала СИТ

Y = k X, (3.1)

где k - реальное значение коэффициента передачи преобразования СИТ, который равняется

k = k_н + k = k_н + k_н_м , (3.2)

где k_н - номинальное значение коэффициента передачи СИТ;

k = k_н_м - абсолютный прирост коэффициента передачи СИТ, обусловленный относительной мультипликативной погрешностью _м.

Рис. 3.1. Структурная схема калибровки СИТ с помощью меры

С учетом равенства (3.2) формула (3.1.) принимает вид

Y = k_нX + k_н_мХ. (3.3)

В режиме калибровки (состояние II переключателя S) на вход измерительного канала СИТ из меры подается строго заданное значение Х₀ физической величины той же природы, что и измеряемая величина X. В этом случае с учетом равенства (3.2) имеем

Y₀ = kX₀ = k_нX₀ + k_н_мХ₀ = Y_н + Y_м ,

где Y_н = k_нX₀ - номинальное значение сигнала измерительной информации Y на выходе СИТ, который отвечает заданному значению образцовой величины меры;

Y_м = k_н_мХ₀ - абсолютная мультипликативная погрешность СИТ.

В процессе калибровки оператор с помощью ручного корректирующего влияния изменяет коэффициент передачи (преобразования) СИТ до тех пор, пока реальное значение сигнала измерительной информации Y будет равняться номинальному значению Y_н, которое отвечает условию Y_м = 0, то есть отсутствию мультипликативной погрешности СИТ. При этом коэффициент передачи СИТ будет номинальным: k_н = Y_н/X₀.

Мультипликативную коррекцию, или калибровку СИТ с помощью образцового измерительного прибора (рис.3.2) рекомендуется проводить при значении заданной входной величины X, близкому к номинальному значению Х_н для данного СИТ. Во время калибровки оператор с помощью ручного корректирующего влияния изменяет коэффициент передачи (преобразования) СИТ до тех пор, пока значение сигналов измерительной информации Y и Y₀ соответственно не совпадут, то есть Y = Y₀ .

Рис.3.2. Структурная схема калибровки СИТ с помощью рабочего эталона

Схема калибровки измерительного преобразователя (или СИТ) с образцовым обратным преобразователем и разностным устройством приведена на рис.3.3. В процессе калибровки оператор с помощью ручного корректирующего влияния изменяет коэффициент преобразования измерительного преобразователя до выполнения условия Х = Х – Х_ооп = 0, где Х_ооп - величина на выходе образцового обратного измерительного преобразователя. При этом , то есть k = k_н .

Рис.3.3 Структурная схема калибровки измерительных преобразователей с образцовым обратным преобразователем

3.3.2. Коррекция погрешностей средств измерительной техники без влияния оператора

Коррекция погрешностей без влияния оператора на СИТ осуществляется или введением оператором поправки в результат измерения, или обработкой оператором нескольких результатов показаний СИТ.

Коррекция погрешности результата измерения введением поправки оператором позволяет исключить систематическую составляющую дополнительной погрешности и может быть использована только в том случае, когда известна зависимость между дополнительной погрешностью и влияющей величиной, которая приводит к этой погрешности. Тогда по этой зависимости оператором вычисляется дополнительная погрешность, например от влияния температуры Y_t , и в неисправленный результат измерения величины вводится поправка П_t на температурную погрешность Y_t (П_t = -Y_t). Получаем уточненный результат измерения

Y = + П_t.

Коррекция погрешности результата измерения обработкой оператором нескольких показаний СИТ используется для исключения как аддитивной, так и мультипликативной погрешностей.

Если СИТ имеет адитивную систематическую погрешность _ад, то при измерении величины X его показания будут равняться

= kX + _ад. (3.4)

Для исключения аддитивной погрешности _ад необходимо провести одно дополнительное измерение при Х = 0, получим показания прибора Y_ад = _ад. Возьмем разницу двух показаний СИТ (или фактически введем в результат измерения поправку П_ад = -_ад), имеем

Y = - Y_ад = kX,

то есть получаем уточненный результат измерения, который не содержит аддитивную систематическую погрешность.

Для СИТ с относительной мультипликативной погрешностью _м для ее исключения проводятся два измерения: измеряемой величины X и образцовой величины Х₀, заданной нерегулируемой мерой. Получают два показания СИТ, которые согласно формуле (3.3) равняются:

_х = k(1 + _м)Х

_х0 = k(1 + _м)Х₀

Измеряемую величину X находят из соотношения

Х = ( _х / _х0 ) Х₀ (3.5)

Если погрешность СИТ имеет аддитивную и мультипликативную составляющие, то для их исключения проводятся два дополнительных измерения: при X₁ = 0 и при Х₂ = Х₀, а потом проводятся вычисления согласно формулам (3.4) и (3.5).

Аддитивная и мультипликативная систематические составляющие погрешности СИТ могут быть одновременно исключены при использовании метода замещения, когда проводятся два цикла измерений. В первом цикле на вход СИТ направляется измеряемая величина X и его показание будет

= k(1 + _м)Х + _ад . (3.6)

Во втором цикле измерений на вход СИТ подается образцовая величина Х₀ из регулируемой меры, регулированием которой устанавливают то же показание СИТ. Если систематические аддитивная и мультипликативная составляющие погрешности СИТ являются постоянными, то это показание равняется

= k(1 + _м)Х₀ + _ад . (3.7)

Из сравнения соотношений (3.6) и (3.7) имеем Х = Х₀.Следовательно, результат измерений не зависит от аддитивной и мультипликативной постоянных систематических составляющих погрешности.

Метод замещения может также использоваться для коррекции низкочастотных (медленно изменяющихся) случайных адитивних и мультипликативных составляющих погрешности СИТ.

Если градуировочная характеристика СИТ является нелинейной, то для коррекции аддитивной и мультипликативной погрешностей необходимо осуществить по меньшей мере три измерения в узком интервале, который охватывает измеряемое значение X. Считая этот интервал градуировочной характеристики линейным, для трех измерений имеем систему уравнений:

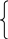
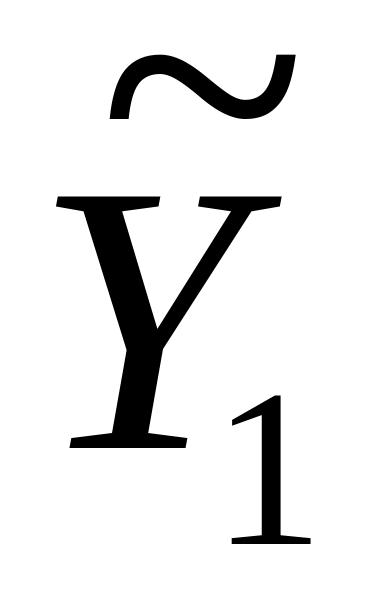= (Х) = kХ + ад ;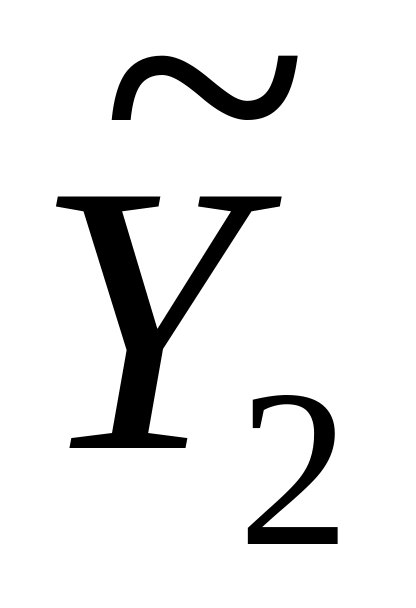 = (Х + Х0) = k(Х + Х0) + ад ; (3.8)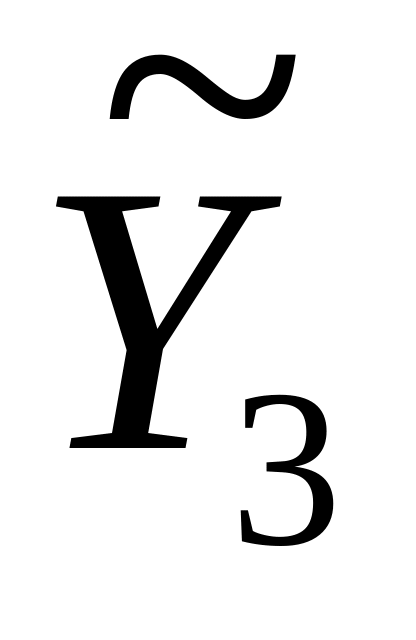 = (Х) = kХ + ад ,

где Х₀ - заданный прирост измеряемой величины X;

 - масштабный коэффициент, близкий к 1;

_ад - аддитивная погрешность измерений.

Решая систему уравнений (3.8) относительно измеряемой величины X, имеем

, (3.9)

откуда видно, что результат измерения X не содержит аддитивной погрешности _ад и коэффициента k, изменение которого связано с мультипликативной погрешностью. (В этой системе вектор неизвестных: { X, _ад, k}).

Ручная коррекция погрешностей СИТ приводит к увеличению времени измерений, поэтому у современных СИТ, особенно цифровых, ее автоматизируют.