10.7. Деформации крыла и особенности работы его корневой части

Крыло рассматривается как балка, защемленная у борта фюзеляжа, за ее упругую ось Z принимается ось жесткости крыла (рис. 10.24).

Деформации крыла характеризуются прогибами “у” его сечений и углами закручивания (рис. 10.25).

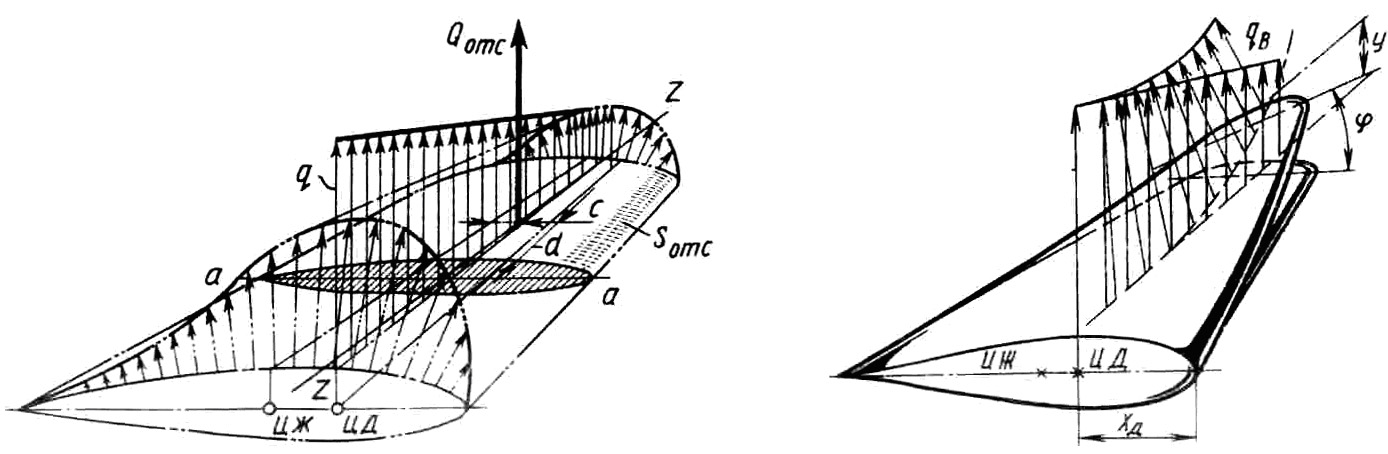
Рис. 10.24. Распределение воздушной нагрузки

по размаху и по хорде крыла

По данным расчета на прочность можно вычислить для сечений крыла значения :

где – модуль упругости для фиктивной прямолинейной диаграммы ; – редуцированный момент инерции всего сечения. Если схематизировать крыло как двухпоясную балку с высотой Н и равными редуцированными площадями поясов (панелей) F, то

Рис. 10.25. Деформация крыла под действием

воздушной нагрузки

Девиация (угол наклона касательной к изогнутой оси) определяется как интеграл функции у":

Прогиб вычисляется как интеграл функции

Обычно аналитических выражений для и от оси Z нет, и интегрирование производится планиметрированием, графическим или численным путем.

Относительный угол закручивания (для однозамкнутого конту- ра) равен

где – криволинейный интеграл, который берется по длине контура сечения; – удвоенная площадь контура; – толщина обшивки. Полный угол закручивания на участке z от борта равен

Интегрирование производится численным способом или графически. Найденные таким образом деформации не учитывают деформаций подфюзеляжной части крыла.

Рассчитывая деформацию стреловидного крыла, следует интегрирование вести вдоль его упругой оси, лежащей в плоскости изгиба.

При определении деформаций кручения нужно учитывать различие значений модуля сдвига G разных элементов крыла.

При расчете крыла обычно принимают следующие допущения:

а) крыло (как и другие тонкостенные конструкции каркаса) работает на сдвиг и кручение в условиях свободной депланаций сечений;

б) деформации, вызванные действием изгибающих моментов, сами по себе подчиняются закону плоских сечений и на депланацию сечений не влияют.

Эксперименты и теоретические исследования подтверждают справедливость этих допущений для концевой части крыла обычной конструкции.

Что касается корневой части крыла, то на ее напряженное состояние при упругой работе крыла оказывает влияние стеснение депланаций, приводящее к возникновению в поперечных сечениях дополнительных нормальных напряжений при работе на сдвиг и кручение (рис. 10.26).

а

б

4

1

2

5

6

3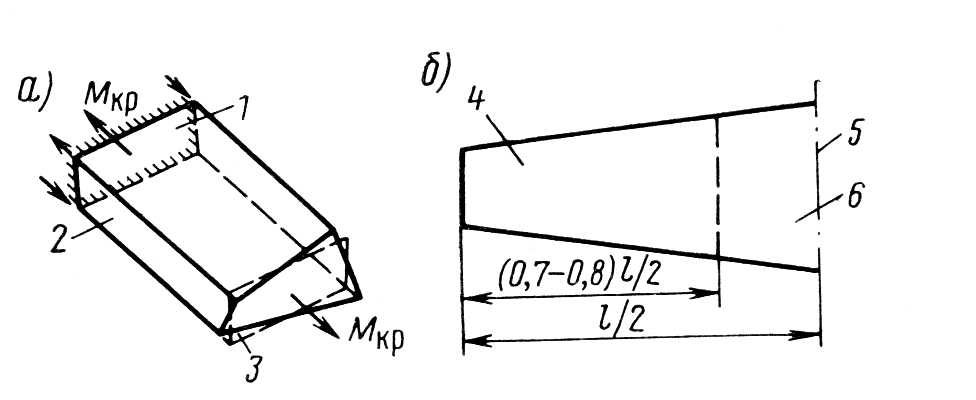

Рис. 10.26. Особенности работы различных участков крыла при кручении [6]:

а, б – схемы депланации сечений:

1 – заделка; 2 – стеснение депланации; 3 – свободная депланация; 4 – зона свободных

депланаций; 5 – полное стеснение депланаций; 6 – частичное стеснение депланаций

На схеме (рис. 10.26, а) показаны дополнительные нормальные усилия в поясах, возникающие в заделке отсека крыла из-за стеснения депланаций, обусловленных кручением. В таких условиях полного стеснения депланаций находится при симметричной нагрузке крыла сечение крыла по плоскости симметрии самолета.

Примыкающий участок крыла работает в условиях частичного стеснения депланаций (рис. 10.26, б).

Распределение усилий в элементах сечения крыла в зоне полного стеснения депланаций сходно с распределением усилий между болтами или заклепками в узловом соединении, метод расчета которого (метод центра жесткости) предложен известным русским инженером В. Г. Шуховым. Метод расчета крыла на стесненное кручение разработан в 1932 г. В. Н. Беляевым.

Необходимо отметить, что при наступлении пластических деформаций указанные выше дополнительные напряжения в элементах корневой части крыла уменьшаются. На основании этого при расчетах на действие расчетной разрушающей нагрузки в случае А и А' можно приближенно не учитывать влияние стеснения депланаций и отклонений от закона плоских сечений.

Как показали исследования, при упругой работе конструкции стреловидного двухлонжеронного или моноблочного крыла вблизи корня возникают значительные дополнительные напряжения из-за отклонения деформаций изгиба от закона плоских сечений. Эти дополнительные напряжения превышают по величине напряжения от стеснения депланаций настолько, что последними при расчете стреловидного крыла можно пренебречь.