10.6. Приближенный расчет крыла на сдвиг и кручение

В приближенном расчете на сдвиг и кручение рассматривается раздельно действие поперечной силы Q, расположенной в центре жесткости сечения, и действие крутящего момента М_кр (рис. 10.21).

Определение касательных напряжений от поперечной силы, приложенной в центре жесткости сечения. Основное допущение, принимаемое при приближенном определении , состоит в предположении, что поперечная сила Q, проходящая через центр жесткости сечения, вызывает касательные напряжения только в стенках. Касательными напряжениями, возникающими при этом в верхней и нижней обшивке, пренебрегают.

ЦЖ

ЦН

ЦЖ

Рис. 10.21. Поперечная сила и крутящий момент

в сечении крыла

Как уже отмечалось, лонжероны в составе балки крыла работают совместно. Поэтому поперечная сила Q, проходящая через центр жесткости сечения, распределяется между лонжеронами пропорционально их изгибным жесткостям.

На этом основании для двухлонжеронного крыла

.

Отсюда

Для многолонжеронного крыла

Погонное касательное усилие в стенке от поперечной силы находится как

q_Qi =

где – рабочая высота лонжерона.

Касательные напряжения в стенках равны

где – площадь сечения стенки, ; – толщина стенки.

Если крыло имеет конусность, то в формулы вводится

где . Конусность крыла спереди характеризуется углом который приближенно находится по формуле

где – угол между осями поясов i-го лонжерона; m – число лонжеронов.

Определение положения центра жесткости сечения. Центр жесткости сечения крыла находится как точка, через которую проходит равнодействующая Q сил Q_i (рис. 10.22). В частности, для двухлонжеронного крыла (рис. 10.22, а) условие равенства моментов относительно первого лонжерона от силы и ее составляющих и имеет вид:

где – расстояние от переднего лонжерона до центра жесткости.

Отсюда

Для трехлонжеронного крыла (рис. 10.22, б) подобным же образом получим

а

б

ЦЖ

ЦЖ

а_ж

а_ж

Рис. 10.22. Схема к определению положения центра жесткости крыла:

а – двухлонжеронного; б – трехлонжеронного

Определение касательных напряжений от крутящего момента. Точные расчеты показывают, что влияние конусности (непараллельности продольных элементов) на распределение усилий от М_кр незначительно. Поэтому М_кр определяется без учета конусности:

где – эпюрное значение поперечной силы (без поправки на конусность); а – расстояние от линии действия силы Q до центра жесткости сечения (см. рис. 10.21).

В расчет на М_кр следует вводить все участки сечения крыла, имеющие замкнутый контур (рис. 10.23).

Сечения хвостовой части крыла обычно не представляют собой замкнутого контура, так как там размещены элероны или элементы механизации крыла.

Носок крыла, если он не имеет вырезы, вводится в расчет. Работой внутренних стенок на М_кр пренебрегают, так как касательные напряжения от кручения в них обычно невелики. Принимают, что М_кр воспринимается внешним замкнутым контуром.

Определение производится по формулам расчета на кручение при свободном искажении:

При подсчете для каждого элемента берется свое значение

Площадь контура подсчитывается по формулам трапеции. Передняя часть спрямляется по форме трапеции, равновеликой площади носка (рис. 10.23, а). Так, для двухлонжеронного крыла

а

б

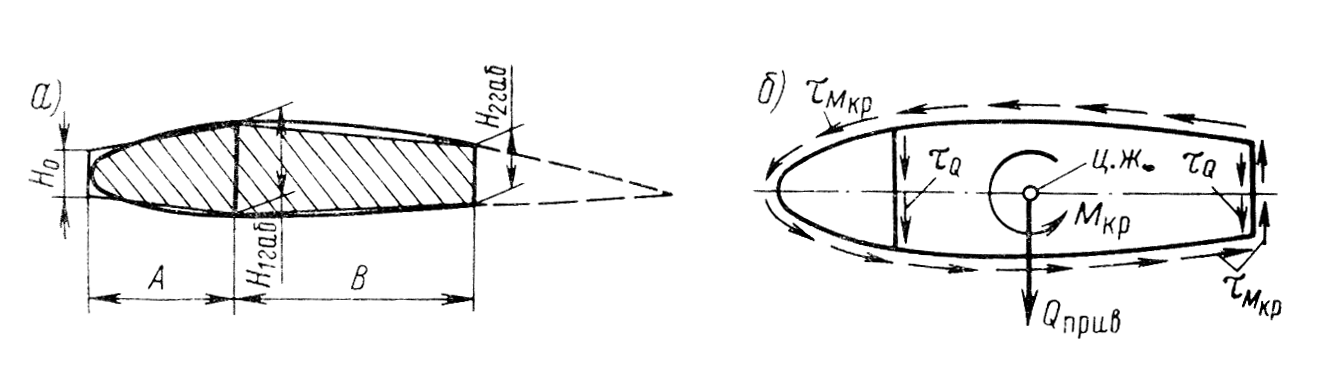
Рис. 10.23. Схема к расчету касательных напряжений:

а – площадь контура сечения; б – поперечная сила, крутящий момент и соответствующие им касательные напряжения в элементах сечения

Если необходимо учесть наличие в сечении нескольких замкнутых контуров, полный крутящий момент можно приближенно распределить между ними пропорционально их крутильным жесткостям с:

где

где S_i – длина участка периметра рассматриваемого контура с толщиной стенки ; G - модуль сдвига.

Тогда погонное касательное усилие в каждом контуре

Величина внутренней стенки находится как разность значений для соседних контуров.

Суммирование погонных касательных усилий и напряжений. Суммарное погонное касательное усилие в элементе контура равно

Суммарное касательное напряжение находится как

Усилия в сечении и напряжения от них показаны на рис. 10.23, б. Для проверки правильности расчета можно использовать условие

.

Проверка прочности. Условие прочности элементов, работающих на сдвиг, выглядит как

Коэффициент избытка прочности равен

Для стенки, нагруженной только , условие прочности на сдвиг является основным. Для обшивки должно быть учтено, что она работает совместно на  и .