
- •III. Основные теоремы о пространствах
- •3.1. Полные метрические пространства
- •1. Из элементов данного неполного метрического пространства построим некоторое пространство .
- •2.2. Независимость от выбора представителей.
- •2.3. Проверим выполнение аксиом метрики.
- •3.2. Понятие меры
- •3.3. Понятие меры Лебега
- •3.4. Понятие измеримой функции
- •3.5. Схема построения интеграла Лебега (На множестве конечной меры)
- •3.6. Конструкция интеграла Лебега
- •3.7. Компактность в метрических пространствах
- •Культурный минимум.
- •Вопросы.
- •Задачи.
3.5. Схема построения интеграла Лебега (На множестве конечной меры)
Разбиение области интегрирования осуществляется по признаку близости значений интегрируемой функции.
1.
Рассматриваются
простые
измеримые функции
 ,
то
есть функции, принимающие
не более чем счетное число значений
,
то
есть функции, принимающие
не более чем счетное число значений , где
, где
 при
.
Для
таких функций под интегралом по множеству
понимается сумма или ряд (при условии
абсолютной сходимости)
при
.
Для
таких функций под интегралом по множеству
понимается сумма или ряд (при условии
абсолютной сходимости)
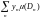 ,
где
,
где
 меры тех отрезков,
на которых функция
принимает значения
меры тех отрезков,
на которых функция
принимает значения
 .
То есть
.
То есть
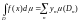 .
.
2. Множество значений
простых
функций,
можно
рассматривать, как метрическое
пространство с метрикой
 .
Но значений не более, чем счётное число,
то есть это множество первой категории,
следовательно, пространство
значений
не полное. Пополнение этого пространства
осуществляется по схеме доказательства
теоремы Хаусдорфа о пополнении
метрического пространства.
.
Но значений не более, чем счётное число,
то есть это множество первой категории,
следовательно, пространство
значений
не полное. Пополнение этого пространства
осуществляется по схеме доказательства
теоремы Хаусдорфа о пополнении
метрического пространства.
4. Из элементов
данного неполного метрического
пространства
строится
полное пространство, где в качестве
классов эквивалентности, объявляется
множество всех почти всюду равных
простых
измеримых функций,
почти всюду (или равномерно) сходящихся
к функции
.
Таким образом мы получили новое фактор
множество
,
элементами которого являются
непересекающиеся классы фундаментальных
последовательностей
представителями которых являются
фундаментальные последовательности
пространства
 .
Если фундаментальная последовательность
сходится к точке
.
Если фундаментальная последовательность
сходится к точке
 ,
то и эквивалентная ей последовательность
сходится к той же точке.
Сходимость
влечёт за собой
существование предела
,
то и эквивалентная ей последовательность
сходится к той же точке.
Сходимость
влечёт за собой
существование предела
 ,
который и объявляется интегралом Лебега
,
который и объявляется интегралом Лебега
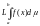 .
.
3.6. Конструкция интеграла Лебега
Пусть
 измеримое множество,
на котором задана ограниченная и
измеримая функция (функционал)
измеримое множество,
на котором задана ограниченная и
измеримая функция (функционал)
 .
.
Обозначив
 ,
а
,
а
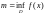
 ,
назовём
,
назовём
 разбиением
произвольное множество точек
разбиением
произвольное множество точек
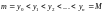 .
.Пусть
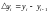 ,
а
,
а
 диаметр разбиения
при фиксированном
диаметр разбиения
при фиксированном
 .
При изменении
или при выборе
других точек разбиения диаметр разбиения
будет меняться.
.
При изменении
или при выборе
других точек разбиения диаметр разбиения
будет меняться.разбиение называется нормальным, если
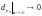 .
.Лебеговым разбиением множества называется кортеж
 ,
где
,
где
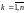 ,
а
,
а
 ,
если
.
Здесь
,
если
.
Здесь
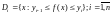 .
.
Пусть
 произвольная точка элемента кортежа
.
Составим сумму
произвольная точка элемента кортежа
.
Составим сумму
 интегральную
сумму Лебега.
интегральную
сумму Лебега.Число
 ,
если оно существует, называется
определённым интегралом Лебега от
ограниченной и измеримой функции
,
заданной на измеримом множестве
,
если для любой нормальной последовательности
,
если оно существует, называется
определённым интегралом Лебега от
ограниченной и измеримой функции
,
заданной на измеримом множестве
,
если для любой нормальной последовательности
 разбиений, любого
выбора точек
разбиений, любого
выбора точек
 и
и
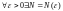 и
и
 и
и
 .
.
Комментарий.
Определение интеграла Лебега аналогично
определению интеграла Римана, но только
интегральные суммы составляются
разбиением не области определения, а
множества значений функции. Если у вас
есть несколько конвертов денег, то
пересчитать их можно или посчитав деньги
в каждом конверте (метод Римана) или
выложить их из конвертов и сгруппировать
по купюрам (метод Лебега). Отсюда ясно,
что функция, интегрируемая по Риману,
будет интегрироваться и по Лебегу и
интегралы будут совпадать. Обратное,
вообще говоря, неверно. Для существования
интеграла Римана необходимо и достаточно
(теорема Дюбуа
Раймона), чтобы множество точек конечного
разрыва имело меру ноль. По Лебегу можно
интегрировать и всюду разрывные функции.
Например, функция Дирихле разрывна во
всех иррациональных точках, то есть
множество точек разрыва имеет меру
один. Она не интегрируема по Риману, но
интегрируема по Лебегу:
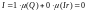 .
Для интеграла Лебега имеют место
свойства, совпадающие с соответствующими
свойствами интеграла Римана с точностью
до формулировок.
.
Для интеграла Лебега имеют место
свойства, совпадающие с соответствующими
свойствами интеграла Римана с точностью
до формулировок.
Примеры.
1.
Взять интеграл Лебега
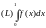 ,
если
,
если

2.
Взять интеграл Лебега
,

3.
Взять интеграл Лебега
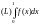 ,
если
,
если

4.
Взять интеграл Лебега
,
 где
где
 - канторов дисконтинуум,
- канторов дисконтинуум,
 - его дополнение до всего отрезка.
- его дополнение до всего отрезка.
5.
Взять интеграл Лебега
,
 где
- канторов дисконтинуум,
- его дополнение до всего отрезка.
где
- канторов дисконтинуум,
- его дополнение до всего отрезка.
6.
Взять интеграл Лебега
,
,
где
- канторов дисконтинуум,
- его дополнение до всего отрезка, а
 - неизмеримое множество.
- неизмеримое множество.
7.
Вычислить с точностью до 0,001 интеграл
Лебега от функции

на
множестве
 ,
полученном удалением из отрезка
,
полученном удалением из отрезка
 интервалов
интервалов
 .
.
Это
множество есть объединение множества
меры ноль, состоящего из точек 0 и 1, и
сегментов
 ,
на каждом из которых функция интегрируема
по Риману.
,
на каждом из которых функция интегрируема
по Риману.

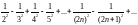
8.
Взять интеграл Лебега
,
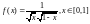 .
Функция
.
Функция
 неотрицательна и непрерывна на своей
области определения, то есть интеграл
Лебега существует, если и только если
существует соответствующий интеграл
Римана.
неотрицательна и непрерывна на своей
области определения, то есть интеграл
Лебега существует, если и только если
существует соответствующий интеграл
Римана.
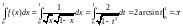 .
.
