III. Основные теоремы о пространствах

Никакие доказательства не имеют заранее установленной силы.

статья 17 УПК РФ

3.1. Полные метрические пространства

Теорема 1 (Критерий полноты Кантора). Метрическое пространство полно, если и только если любая последовательность непустых вложенных замкнутых шаров, радиусы которых стремятся к нулю, имеет непустое пересечение.

Необходимость. .Пусть последовательность вложенных шаров при и пространство полное. Тогда существует и единственна точка , принадлежащая всем шарам сразу. Рассмотрим последовательность центров этих шаров и оценим расстояние при m>n. Так как при m>n , но по условию теоремы , стало быть и при . То есть последовательность фундаментальна и силу полноты пространства сходится. Члены её, начиная с m-го, принадлежат шару , а так как шар замкнутый, то и предел принадлежит этому шару, а , то есть пересечение шаров не пусто.

Достаточность. Пусть - произвольная фундаментальная последовательность в пространстве . Будем полагать, что это последовательность центров замкнутых шаров и покажем её сходимость, то есть полноту пространства . Выделим из последовательности подпоследовательность , такую, что Покажем, что подпоследовательность замкнутых шаров является последовательностью вложенных шаров, т.е. при m>k . Действительно, пусть произвольная точка х принадлежит шару . Тогда Из неравенства треугольника найдём, что . ( )Таким образом, точка х принадлежит и шару . Стало быть, шары вложены друг в друга. По условию теоремы последовательность вложенных шаров имеет непустое пересечение. Пусть – общая точка всех шаров. Поскольку радиусы вложенных шаров стремятся к нулю, то т.е. подпоследовательность сходится к точке . Тогда и сама фундаментальная последовательность ( ) сходится к той же точке . Действительно, согласно неравенству треугольника имеем При этом так как подпоследовательность сходится к . Тогда т.е. последовательность сходится.

Комментарий. Нарушение любых условий теоремы приводит к тому, что пересечение шаров пусто. В пункте 2.5.3. было рассмотрено метрическое пространство . Это пространство полное, фундаментальные последовательности здесь может быть только стационарными. а они сходится.

Возьмём последовательность шаров 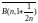: Очевидно, это последовательность замкнутых вложенных шаров, но их пересечение пусто: .

Пример. Может ли в банаховом пространстве иметь пустое пересечение последовательность непустых вложенных замкнутых множеств? Да, может. Рассмотрим банахово пространство вещественных чисел и последовательность непустых замкнутых вложенных множеств в нем . Ясно, что .

Определение 1. Пусть множество , где носитель метрического пространства . Множество называется множеством I категории, если его можно представить в виде объединения не более, чем счётного числа нигде не плотных множеств. Остальные множества называются множествами II категории.

Пример. Множество рациональных чисел есть множество I категории.

Теорема 2 (Бэра о категориях). Носитель полного метрического пространства есть множество II категории.

Пусть Носитель полного метрического пространства есть множество I категории, то есть , где нигде не плотные в множества. Пусть – некоторый замкнутый шар радиуса 1. Так как нигде не плотное множество, оно не плотно и в , то есть существует замкнутый шар радиуса менее такой, что и . Поскольку множество нигде не плотно, то существует замкнутый шар радиуса менее , для которого . И так далее. В результате образуется последовательность вложенных замкнутых шаров полного метрического пространства , радиусы которых стремятся к нулю. Тогда по теореме 1 существует точка , принадлежащая всем шарам сразу. Но по построению , то есть , следовательно .

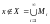Комментарий. Ясно, что в полном метрическом пространстве всякое не пустое открытое множество есть множество второй категории, а множества, дополнительные к множествам первой категории, тоже множества второй категории.

Определение 2. Полное метрическое пространство называется пополнением метрического пространства , если пространство всюду плотно в пространстве .

Определение 3. Пространства и называют изомерными, если между ними существует хоть одна биекция и .

Теорема 3 (Хаусдорфа о пополнении метрических пространств). Любое неполное метрическое пространство имеет единственное с точностью до изомерности пополнение.