Задание

1) Разрезать граф G (рис. 2) на три куска по четыре вершины в каждом.

2) Определить коэффициент разрезания.

3) Сравнить полученный результат с результатами выполнения практических работ №№ 3, 4.

Решение

1) Построить стандартную матрицу F, выделив в ней единичные подматрицы, соответствующие заданному разрезанию графа.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	1	1	1	1	0	0	0	0	0	0	0	0
	2	r2	1	1	1	1	0	0	0	0	0	0	0	0
	3	r3	1	1	1	1	0	0	0	0	0	0	0	0
	4	r4	1	1	1	1	0	0	0	0	0	0	0	0
	5	r5	0	0	0	0	1	1	1	1	0	0	0	0
F =	6	c1	0	0	0	0	1	1	1	1	0	0	0	0	(2)
	7	c2	0	0	0	0	1	1	1	1	0	0	0	0
	8	vd1	0	0	0	0	1	1	1	1	0	0	0	0
	9	vd2	0	0	0	0	0	0	0	0	1	1	1	1
	10	vd3	0	0	0	0	0	0	0	0	1	1	1	1
	11	vt1	0	0	0	0	0	0	0	0	1	1	1	1
	12	vs1	0	0	0	0	0	0	0	0	1	1	1	1

2) Построить матрицу смежности R и разбить её на подматрицы в соответствии с разбиением матрицы F.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	0	0	0	1	0	0	0	0
	2	r2	0	0	0	0	0	0	0	0	0	0	0	1
	3	r3	0	0	0	0	0	0	0	0	0	0	1	1
	4	r4	0	0	0	0	0	0	1	0	0	1	0	0
	5	r5	0	0	0	0	0	0	1	0	0	0	0	2
R =	6	c1	0	0	0	0	0	0	1	0	1	0	1	0	(3)
	7	c2	0	0	0	1	1	1	0	0	0	0	0	1
	8	vd1	1	0	0	0	0	0	0	0	1	0	1	0
	9	vd2	0	0	0	0	0	1	0	1	0	0	0	0
	10	vd3	0	0	0	1	0	0	0	0	0	0	1	0
	11	vt1	0	0	1	0	0	1	0	1	0	1	0	0
	12	vs1	0	1	1	0	2	0	1	0	0	0	0	0

Указанному разрезанию матрицы смежности R соответствует разрезание графа G, показанное на рис. 3. Общее количество рёбер внутри кусков L = 3, а количество внешних связей между кусками K = 13. Коэффициент разрезания графа (G) = 3/13 = 0,23.

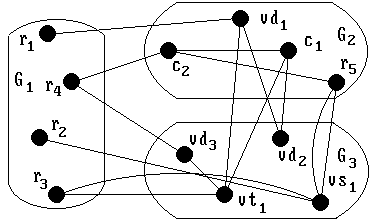
Рис. 3. Разрезание графа, соответствующее разрезанию матрицы смежности (3)

Для максимизации функции L необходимо выполнить перестановки строк и столбцов матрицы смежности (3). С этой целью вводятся некоторые вспомогательные матрицы

3) Построить вспомогательную матрицу M = m_ij_n, где i, j  J = {1, 2, …, n}, как результат умножения матриц F и R:

M = F  R (4)

Элементы матрицы M вычисляются по формулам:

m_ij = , m_ji = (5)

Для рассматриваемого графа G матрица M будет иметь вид:

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	0	0	1	1	0	1	1	2
	2	r2	0	0	0	0	0	0	1	1	0	1	1	2
	3	r3	0	0	0	0	0	0	1	1	0	1	1	2
	4	r4	0	0	0	0	0	0	1	1	0	1	1	2
	5	r5	1	0	0	1	1	1	2	0	2	0	2	3
M =	6	c1	1	0	0	1	1	1	2	0	2	0	2	3	(6)
	7	c2	1	0	0	1	1	1	2	0	2	0	2	3
	8	vd1	1	0	0	1	1	1	2	0	2	0	2	3
	9	vd2	0	1	2	1	2	2	1	2	0	1	1	0
	10	vd3	0	1	2	1	2	2	1	2	0	1	1	0
	11	vt1	0	1	2	1	2	2	1	2	0	1	1	0
	12	vs1	0	1	2	1	2	2	1	2	0	1	1	0

Ниже приведены примеры использования формул (5) для вычисления некоторых значений элементов матрицы M.

m₁₁ = f₁₁  (r₁, r₁) + f₁₂  (r₁, r₂) + f₁₃  (r₁, r₃) + f₁₄  (r₁, r₄) + f₁₅  (r₁, r₅) +

+ f₁₆  (r₁, c₁) + f₁₇  (r₁, c₂) + f₁₈  (r₁, vd₁) + f₁₉  (r₁, vd₂) + f₁₁₀  (r₁, vd₃) +

+ f₁₁₁  (r₁, vt₁) + f₁₁₂  (r₁, vs₁) =

= 1  0 + 1  0 + 1  0 + 1  0 + 0  0 + 0  0 + 0  1 + 0  1 + 0  0 + 0  1 + 0  2 = 0

m₁₇ = f₁₁  (c₂, r₁) + f₁₂  (c₂, r₂) + f₁₃  (c₂, r₃) + f₁₄  (c₂, r₄) + f₁₅  (c₂, r₅) +

+ f₁₆  (c₂, c₁) + f₁₇  (c₂, c₂) + f₁₈  (c₂, vd₁) + f₁₉  (c₂, vd₂) + f₁₁₀  (c₂, vd₃) +

+ f₁₁₁  (c₂, vt₁) + f₁₁₂  (c₂, vs₁) =

= 1  0 + 1  0 + 1  0 + 1  1 + 0  1 + 0  1 + 0  0 + 0  0 + 0  0 + 0  0 + 0  1 = 1

…

m₁₁₂ = f₁₁  (vs₁, r₁) + f₁₂  (vs₁, r₂) + f₁₃  (vs₁, r₃) + f₁₄  (vs₁, r₄) + f₁₅  (vs₁, r₅) +

+ f₁₆  (vs₁, c₁) + f₁₇  (vs₁, c₂) + f₁₈  (vs₁, vd₁) + f₁₉  (vs₁, vd₂) + f₁₁₀  (vs₁, vd₃) +

+ f₁₁₁  (vs₁, vt₁) + f₁₁₂  (vs₁, vs₁) =

= 1  0 + 1  1 + 1  1 + 1  0 + 0  2 + 0  0 + 0  1 + 0  0 + 0  0 + 0  0 + 0  0 = 2

…

m₈₁₂ = f₈₁  (vs₁, r₁) + f₈₂  (vs₁, r₂) + f₈₃  (vs₁, r₃) + f₈₄  (vs₁, r₄) + f₈₅  (vs₁, r₅) +

+ f₈₆  (vs₁, c₁) + f₈₇  (vs₁, c₂) + f₈₈  (vs₁, vd₁) + f₈₉  (vs₁, vd₂) + f₈₁₀  (vs₁, vd₃) +

+ f₈₁₁  (vs₁, vt₁) + f₈₁₂  (vs₁, vs₁) =

= 0  0 + 0  1 + 0  1 + 0  0 + 1  2 + 1  0 + 1  1 + 1  0 + 0  0 + 0  0 + 0  0 +

+ 0  0 = 2 +1 = 3

…

Процесс продолжается до тех пор, пока не будут найдены все элементы матрицы M. Матрица M не является симметричной, т.е. в общем случае m_ij m_ji.

4) Построить вспомогательную матрицу B = ||b_ij||_n, где i, j  J = {1, 2, …, n}. Матрица B представляет собой результат поэлементного перемножения матриц F и R:

B = F  R (7)

где F – инверсия матрицы F, т.е. каждый единичный элемент матрицы F заменяется на нулевой и наоборот.

Для рассматриваемого примера матрица F имеет вид:

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	1	1	1	1	1	1	1	1
	2	r2	0	0	0	0	1	1	1	1	1	1	1	1
	3	r3	0	0	0	0	1	1	1	1	1	1	1	1
	4	r4	0	0	0	0	1	1	1	1	1	1	1	1
	5	r5	1	1	1	1	0	0	0	0	1	1	1	1
F =	6	c1	1	1	1	1	0	0	0	0	1	1	1	1	(8)
	7	c2	1	1	1	1	0	0	0	0	1	1	1	1
	8	vd1	1	1	1	1	0	0	0	0	1	1	1	1
	9	vd2	1	1	1	1	1	1	1	1	0	0	0	0
	10	vd3	1	1	1	1	1	1	1	1	0	0	0	0
	11	vt1	1	1	1	1	1	1	1	1	0	0	0	0
	12	vs1	1	1	1	1	1	1	1	1	0	0	0	0

Элемент b_ij матрицы B определяется по формуле:

b_ij = f_ij  r_ij (9)

где f_ij – элемент матрицы F.

Элементы первой строки матрицы B равны:

b₁₁ = f₁₁  (r₁, r₁) = 0; b₁₂ = f₁₂  (r₁, r₂) = 0; b₁₃ = f₁₃  (r₁, r₃) = 0;

b₁₄ = f₁₄  (r₁, r₄) = 0; b₁₅ = f₁₅  (r₁, r₅) = 0; b₁₆ = f₁₆  (r₁, c₁) = 0;

b₁₇ = f₁₁  (r₁, c₂) = 0; b₁₈ = f₁₈  (r₁, vd₁) = 1; b₁₉ = f₁₉  (r₁, vd₂) = 0;

b₁₁₀ = f₁₁₀  (r₁, vd₃) = 0; b₁₁₁ = f₁₁₁  (r₁, vt₁) = 0; b₁₁₂ = f₁₁₂  (r₁, vs₁) = 0;

Аналогично определяются все остальные элементы матрицы. В результате будет получена вспомогательная матрица B:

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	0	0	0	1	0	0	0	0
	2	r2	0	0	0	0	0	0	0	0	0	0	0	1
	3	r3	0	0	0	0	0	0	0	0	0	0	1	1
	4	r4	0	0	0	0	0	0	1	0	0	1	0	0
	5	r5	0	0	0	0	0	0	0	0	0	0	0	2
B =	6	c1	0	0	0	0	0	0	0	0	1	0	1	0	(10)
	7	c2	0	0	0	1	0	0	0	0	0	0	0	1
	8	vd1	1	0	0	0	0	0	0	0	1	0	1	0
	9	vd2	0	0	0	0	0	1	0	1	0	0	0	0
	10	vd3	0	0	0	1	0	0	0	0	0	0	0	0
	11	vt1	0	0	1	0	0	1	0	1	0	0	0	0
	12	vs1	0	1	1	0	2	0	1	0	0	0	0	0

Матрица B является симметричной относительно главной диагонали: b_ij=b_ji.

5) Построить вспомогательную матрицу P = p_ij_n, где i, j  J = {1, 2, …, n}. Матрица P определяется с помощью матриц M и B по формулам:

p_ij = m_ij – b_ij; p_ij = m_ij – b_ij (11)

Как следует из (11), матрица P не является симметричной.

Для рассматриваемого примера матрица P будет иметь вид:

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	0	0	1	0	0	1	1	2
	2	r2	0	0	0	0	0	0	1	1	0	1	1	1
	3	r3	0	0	0	0	0	0	1	1	0	1	0	1
	4	r4	0	0	0	0	0	0	0	1	0	0	1	2
	5	r5	1	0	0	1	1	1	2	0	2	0	2	1
P =	6	c1	1	0	0	1	1	1	2	0	1	0	1	3	(12)
	7	c2	1	0	0	0	1	1	2	0	2	0	2	2
	8	vd1	0	0	0	1	1	1	2	0	1	0	1	3
	9	vd2	0	1	2	1	2	1	1	1	0	1	1	0
	10	vd3	0	1	2	0	2	2	1	2	0	1	1	0
	11	vt1	0	1	1	1	2	1	1	1	0	1	1	0
	12	vs1	0	0	1	1	0	2	0	2	0	1	1	0

6) Для максимизации значения функции (1) после случайного разрезания графа необходимо выбрать пару вершин, принадлежащих разным кускам графа и переставить их, если значение L при этом увеличивается. Перестановочные коэффициенты определяются по формуле:

_ij = p_ij + p_ji – (p_ii + p_jj) (13)

Следует заметить, что вершины x_i и x_j принадлежат разным кускам. Отсюда следует, что первые два члена выражения (13) характеризуют внешние связи между кусками, а вторые два (в скобках) – внутренние. В таком случае положительное максимальное значение _ij является условием для перестановки вершин из одного куска в другой. Для определения перестановочных коэффициентов целесообразно построить матрицу H = _ij_n, где i, j  J = {1, 2, …, n}. Так как матрица H строится только по результатам операций с элементами симметричной матрицы P, то матрица H также будет симметричной, поэтому достаточно построить только треугольную полуматрицу.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vd1	vd2	vd3	vt1	vs1
	1	r1	0	0	0	0	0	0	0	0	0	0	0	+2
	2	r2		0	0	0	-1	-1	-1	+1	+1	+1	+1	+1
	3	r3			0	0	-1	-1	-1	+1	+2	+2	0	+2
	4	r4				0	0	0	-2	+2	+1	-1	+1	+3
	5	r5					0	0	0	0	+1	0	+2	0
H =	6	c1						0	0	0	+1	0	0	+4	(14)
	7	c2							0	0	+1	-2	0	0
	8	vd1								0	+2	+1	+1	+5
	9	vd2									0	0	0	0
	10	vd3										0	0	0
	11	vt1											0	0
	12	vs1												0

Наибольшее положительное значение имеет элемент _8-12, расположенный на пересечении строки vd₁ и столбца vs₁. После перемещения вершины vd₁ из куска G₂ в кусок G₃, а вершины vs₁ – из куска G₃ в кусок G₂ общее количество L рёбер внутри кусков увеличится на и 5 станет равным 8. Соответственно количество внешних связей K между кусками графа уменьшится и станет равным 8 (рис. 4). Коэффициент разрезания графа G = 8/8 = 1.

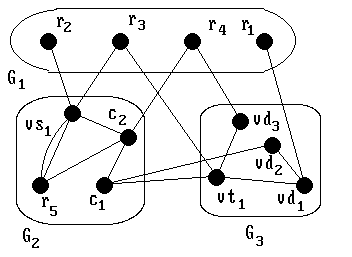
Рис. 4. Разрезание графа G после перестановки вершин vd₁ и vs₁

7) Переставить строки и столбцы vd₁ и vs₁ в матрице смежности (5.3). В результате будет получена матрица R⁽¹⁾:

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vs1	vd2	vd3	vt1	vd1
	1	r1	0	0	0	0	0	0	0	0	0	0	0	1
	2	r2	0	0	0	0	0	0	0	1	0	0	0	0
	3	r3	0	0	0	0	0	0	0	1	0	0	1	0
	4	r4	0	0	0	0	0	0	1	0	0	1	0	0
	5	r5	0	0	0	0	0	0	1	2	0	0	0	0
R(1) =	6	c1	0	0	0	0	0	0	1	0	1	0	1	0	(15)
	7	c2	0	0	0	1	1	1	0	1	0	0	0	0
	8	vs1	0	1	1	0	2	0	1	0	0	0	0	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	1
	10	vd3	0	0	0	1	0	0	0	0	0	0	1	0
	11	vt1	0	0	1	0	0	1	0	0	0	1	0	1
	12	vd1	1	0	0	0	0	0	0	0	1	0	1	0

8) По матрицам F (2) и R⁽¹⁾ (15) построить вспомогательную матрицу M⁽¹⁾. Матрица F будет оставаться неизменной до полного окончания процесса разрезания графа.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vs1	vd2	vd3	vt1	vd1
	1	r1	0	0	0	0	0	0	1	2	0	1	1	1
	2	r2	0	0	0	0	0	0	1	2	0	1	1	1
	3	r3	0	0	0	0	0	0	1	2	0	1	1	1
	4	r4	0	0	0	0	0	0	1	2	0	1	1	1
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
M(1) =	6	c1	0	1	1	1	3	1	3	3	1	0	1	0	(16)
	7	c2	0	1	1	1	3	1	3	3	1	0	1	0
	8	vs1	0 1	1 0	1 1	1 1	3	1	3	3	1	0	1	0
	9	vd2					0	2	0	0	1	1	2	2
	10	vd3	1	0	1	1	0	2	0	0	1	1	2	2
	11	vt1	1	0	1	1	0	2	0	0	1	1	2	2
	12	vd1	1	0	1	1	0	2	0	0	1	1	2	2

9) Построить вспомогательную матрицу B⁽¹⁾, используя матрицы F и R⁽¹⁾. Матрица F является инверсией матрицы F, поэтому она также будет неизменной до окончания решения задачи.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vs1	vd2	vd3	vt1	vd1
	1	r1	0	0	0	0	0	0	0	0	0	0	0	1
	2	r2	0	0	0	0	0	0	0	1	0	0	0	0
	3	r3	0	0	0	0	0	0	0	1	0	0	0	0
	4	r4	0	0	0	0	0	0	1	0	0	1	0	0
	5	r5	0	0	0	0	0	0	0	0	0	0	0	0
B(1) =	6	c1	0	0	0	0	0	0	0	0	1	0	1	0	(17)
	7	c2	0	0	0	1	0	0	0	0	0	0	0	0
	8	vs1	0	1	1	0	0	0	0	0	0	0	0	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	0
	10	vd3	0	0	0	1	0	0	0	0	0	0	0	0
	11	vt1	0	0	1	0	0	1	0	0	0	0	0	0
	12	vd1	1	0	0	0	0	0	0	0	0	0	0	0

10) По матрицам M⁽¹⁾ и B⁽¹⁾, руководствуясь формулой (11), построить вспомогательную матрицу P⁽¹⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vs1	vd2	vd3	vt1	vd1
	1	r1	0	0	0	0	0	0	1	2	0	1	1	0
	2	r2	0	0	0	0	0	0	1	1	0	1	1	1
	3	r3	0	0	0	0	0	0	1	1	0	1	1	1
	4	r4	0	0	0	0	0	0	0	1	0	0	1	1
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
P(1) =	6	c1	0	1	1	1	3	1	3	3	0	0	0	0	(18)
	7	c2	0	1	1	0	3	1	3	3	1	0	1	0
	8	vs1	0	0	0	1	3	1	3	3	1	0	1	0
	9	vd2	1	0	1	1	0	1	0	0	1	1	2	2
	10	vd3	1	0	1	0	0	2	0	0	1	1	2	2
	11	vt1	1	0	0	1	0	1	0	0	1	1	2	2
	12	vd1	0	0	1	1	0	2	0	0	1	1	2	2

11) По формуле (13) определить перестановочные коэффициенты и построить полуматрицу H⁽¹⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			r1	r2	r3	r4	r5	c1	c2	vs1	vd2	vd3	vt1	vd1
	1	r1	0	0	0	0	-3	-1	-2	-1	0	+1	0	-2
	2	r2		0	0	0	-2	0	-1	-2	-1	0	-1	-2
	3	r3			0	0	-2	0	-1	-2	0	+1	0	0
	4	r4				0	-2	0	-3	-1	0	-1	0	0
	5	r5					0	0	0	0	-2	-4	-4	-5
H(1) =	6	c1						0	0	0	0	0	-2	-1	(19)
	7	c2							0	0	-3	-4	-4	-5
	8	vs1								0	-3	-4	-4	-5
	9	vd2									0	0	0	0
	10	vd3										0	0	0
	11	vt1											0	0
	12	vd1												0

В полученной матрице (19) отыскать перестановочный коэффициент _ij с максимальным положительным значением. Таких коэффициентов два: _1-10 и _3-10. Отсюда следует, что перестановке подлежит одна из двух пар вершин: r₁ и vd₃ или r₃ и vd₃. Из этих двух пар вершин выбираем ту пару, у которой сумма локальных степеней меньше. Так как (r₁) = 1 < (r₃) = 2, то для перестановки выбираем вершины r₁ и vd₃. В результате получим новый вариант разрезания графа (рис. 5).

Рис. 5. Результат разрезания графа G после перестановки вершин vd₃ и r₁.

Общее количество рёбер L внутри кусков увеличилось до 9, а количество внешних связей между кусками уменьшилось до 7. Коэффициент разрезания графа (G) = 9/7 = 1,29.

12) Переставить в матрице R⁽¹⁾ (15) строки и столбцы r₁ и vd₃. В результате получим матрицу R⁽²⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	r2	r3	r4	r5	c1	c2	vs1	vd2	r1	vt1	vd1
	1	vd3	0	0	0	1	0	0	0	0	0	0	1	0
	2	r2	0	0	0	0	0	0	0	1	0	0	0	0
	3	r3	0	0	0	0	0	0	0	1	0	0	1	0
	4	r4	1	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	1	2	0	0	0	0
R(2) =	6	c1	0	0	0	0	0	0	1	0	1	0	1	0	(20)
	7	c2	0	0	0	1	1	1	0	1	0	0	0	0
	8	vs1	0	1	1	0	2	0	1	0	0	0	0	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	1
	10	r1	0	0	0	0	0	0	0	0	0	0	0	1
	11	vt1	1	0	1	0	0	1	0	0	0	0	0	1
	12	vd1	0	0	0	0	0	0	0	0	1	1	1	0

13) По матрице смежности R⁽²⁾ и стандартной матрице F построить вспомогательную матрицу M⁽²⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	r2	r3	r4	r5	c1	c2	vs1	vd2	r1	vt1	vd1
	1	vd3	1	0	0	1	0	0	1	2	0	0	2	0
	2	r2	1	0	0	1	0	0	1	2	0	0	2	0
	3	r3	1	0	0	1	0	0	1	2	0	0	2	0
	4	r4	1	0	0	1	0	0	1	2	0	0	2	0
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
M(2) =	6	c1	0	1	1	1	3	1	3	3	1	0	1	0	(21)
	7	c2	0	1	1	1	3	1	3	3	1	0	1	0
	8	vs1	0	1	1	1	3	1	3	3	1	0	1	0
	9	vd2	1	0	1	0	0	2	0	0	1	1	1	3
	10	r1	1	0	1	0	0	2	0	0	1	1	1	3
	11	vt1	1	0	1	0	0	2	0	0	1	1	1	3
	12	vd1	1	0	1	0	0	2	0	0	1	1	1	3

14) По матрице смежности R⁽²⁾ и инверсии F стандартной матрицы F построить вспомогательную матрицу B⁽²⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	r2	r3	r4	r5	c1	c2	vs1	vd2	r1	vt1	vd1
	1	vd3	0	0	0	0	0	0	0	0	0	0	1	0
	2	r2	0	0	0	0	0	0	0	1	0	0	0	0
	3	r3	0	0	0	0	0	0	0	1	0	0	1	0
	4	r4	0	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	0	0	0	0	0	0
B(2) =	6	c1	0	0	0	0	0	0	0	0	1	0	1	0	(22)
	7	c2	0	0	0	0	0	0	0	0	0	0	0	0
	8	vs1	0	1	1	0	0	0	0	0	0	0	0	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	0
	10	r1	0	0	0	0	0	0	0	0	0	0	0	0
	11	vt1	1	0	1	0	0	1	0	0	0	0	0	0
	12	vd1	0	0	0	0	0	0	0	0	0	0	0	0

15) По матрицам M⁽²⁾ и B⁽²⁾ построить вспомогательную матрицу P⁽²⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	r2	r3	r4	r5	c1	c2	vs1	vd2	r1	vt1	vd1
	1	vd3	1	0	0	1	0	0	1	2	0	0	1	0
	2	r2	1	0	0	1	0	0	1	1	0	0	2	0
	3	r3	1	0	0	1	0	0	1	1	0	0	1	0
	4	r4	1	0	0	1	0	0	0	2	0	0	2	0
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
P(2) =	6	c1	0	1	1	1	3	1	3	3	0	0	0	0	(23)
	7	c2	0	1	1	1	3	1	3	3	1	0	1	0
	8	vs1	0	1	1	1	3	1	3	3	1	0	1	0
	9	vd2	1	0	1	0	0	1	0	0	1	1	1	3
	10	r1	1	0	1	0	0	2	0	0	1	1	1	3
	11	vt1	0	0	0	0	0	1	0	0	1	1	1	3
	12	vd1	1	0	1	0	0	2	0	0	1	1	1	3

16) Построить полуматрицу перестановочных коэффициентов H⁽²⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	r2	r3	r4	r5	c1	c2	vs1	vd2	r1	vt1	vd1
	1	vd3	0	0	0	0	-4	-2	-3	-2	-1	-1	-1	-3
	2	r2		0	0	0	-2	0	-1	-1	-1	-1	+1	-3
	3	r3			0	0	-2	0	-1	-1	0	0	0	-2
	4	r4				0	-3	-1	-3	-1	-2	-2	0	-4
	5	r5					0	0	0	0	-4	-4	-3	-6
H(2) =	6	c1						0	0	0	-1	0	-1	-2	(24)
	7	c2							0	0	-3	-4	-3	-6
	8	vs1								0	-3	-4	-3	-6
	9	vd2									0	0	0	0
	10	r1										0	0	0
	11	vt1											0	0
	12	vd1												0

В полученной матрице имеется единственный перестановочный коэффициент ₂₁₁, расположенный на пересечении строки r₂ и столбца vt₁. Это означает, что для максимизации функции L необходимо вершину r₂ из куска G₁ переместить в кусок G₃, а вершину vt₁ – из куска G₃ в кусок G₁. После такой перестановки разрезание графа будет иметь вид (рис. 6):

Рис. 6. Результат разрезания графа после перестановки вершин r₂ и vt₁.

Общее количество рёбер внутри кусков L = 10, количество внешних связей K = 6. Коэффициент разбиения графа (G) = 10/6 = 1,67.

17) Переставить в матрице смежности R⁽²⁾ строки и столбцы r₂ и vt₁. В результате матрица смежности примет вид:

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	c1	c2	vs1	vd2	r1	r2	vd1
	1	vd3	0	1	0	1	0	0	0	0	0	0	0	0
	2	vt1	1	0	1	0	0	1	0	0	0	0	0	1
	3	r3	0	1	0	0	0	0	0	1	0	0	0	0
	4	r4	1	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	1	2	0	0	0	0
R(3) =	6	c1	0	1	0	0	0	0	1	0	1	0	0	0	(25)
	7	c2	0	0	0	1	1	1	0	1	0	0	0	0
	8	vs1	0	0	1	0	2	0	1	0	0	0	1	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	1
	10	r1	0	0	0	0	0	0	0	0	0	0	0	1
	11	r2	0	0	0	0	0	0	0	1	0	0	0	0
	12	vd1	0	1	0	0	0	0	0	0	1	1	0	0

18) По матрице смежности R⁽³⁾ и стандартной матрице F построить вспомогательную матрицу M⁽³⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	c1	c2	vs1	vd2	r1	r2	vd1
	1	vd3	2	2	1	1	0	1	1	1	0	0	0	1
	2	vt1	2	2	1	1	0	1	1	1	0	0	0	1
	3	r3	2	2	1	1	0	1	1	1	0	0	0	1
	4	r4	2	2	1	1	0	1	1	1	0	0	0	1
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
M(3) =	6	c1	0	1	1	1	3	1	3	3	1	0	1	0	(26)
	7	c2	0	1	1	1	3	1	3	3	1	0	1	0
	8	vs1	0	1	1	1	3	1	3	3	1	0	1	0
	9	vd2	0	1	0	0	0	1	0	1	1	1	0	2
	10	r1	0	1	0	0	0	1	0	1	1	1	0	2
	11	r2	0	1	0	0	0	1	0	1	1	1	0	2
	12	vd1	0	1	0	0	0	1	0	1	1	1	0	2

19) По матрице смежности R⁽³⁾ и инверсии F стандартной матрицы F построить вспомогательную матрицу B⁽³⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	c1	c2	vs1	vd2	r1	r2	vd1
	1	vd3	0	0	0	0	0	0	0	0	0	0	0	0
	2	vt1	0	0	0	0	0	1	0	0	0	0	0	1
	3	r3	0	0	0	0	0	0	0	1	0	0	0	0
	4	r4	0	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	0	0	0	0	0	0
B(3)=	6	c1	0	1	0	0	0	0	0	0	1	0	0	0	(27)
	7	c2	0	0	0	1	0	0	0	0	0	0	0	0
	8	vs1	0	0	1	0	0	0	0	0	0	0	1	0
	9	vd2	0	0	0	0	0	1	0	0	0	0	0	0
	10	r1	0	0	0	0	0	0	0	0	0	0	0	0
	11	r2	0	0	0	0	0	0	0	1	0	0	0	0
	12	vd1	0	1	0	0	0	0	0	0	0	0	0	0

20) По матрицам M⁽³⁾ и B⁽³⁾ построить вспомогательную матрицу P⁽³⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	c1	c2	vs1	vd2	r1	r2	vd1
	1	vd3	2	2	1	1	0	1	1	1	0	0	0	1
	2	vt1	2	2	1	1	0	0	1	1	0	0	0	0
	3	r3	2	2	1	1	0	1	1	0	0	0	0	1
	4	r4	2	2	1	1	0	1	0	1	0	0	0	1
	5	r5	0	1	1	1	3	1	3	3	1	0	1	0
P(3)=	6	c1	0	0	1	1	3	1	3	3	0	0	1	0	(28)
	7	c2	0	1	1	1	3	1	3	3	1	0	1	0
	8	vs1	0	1	0	1	3	1	3	3	1	0	0	0
	9	vd2	0	1	0	0	0	0	0	1	1	1	0	2
	10	r1	0	1	0	0	0	1	0	1	1	1	0	2
	11	r2	0	1	0	0	0	1	0	0	1	1	0	2
	12	vd1	0	0	0	0	0	1	0	1	1	1	0	2

21) По матрице R⁽³⁾, используя (13), построить полуматрицу перестановочных коэффициентов H⁽³⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	c1	c2	vs1	vd2	r1	r2	vd1
	1	vd3	0	0	0	0	0	-2	-4	-4	-3	-3	-2	-3
	2	vt1		0	0	0	-5	-3	-4	-4	-3	-3	-2	-4
	3	r3			0	0	-3	0	-2	-4	-2	-2	-1	-2
	4	r4				0	-3	0	-4	-2	-2	-2	-1	-2
	5	r5					0	0	0	0	-3	-4	-2	-5
H(3)=	6	c1						0	0	0	-2	-1	+1	-3	(29)
	7	c2							0	0	-3	-4	-2	-5
	8	vs1								0	-2	-3	-2	-4
	9	vd2									0	0	0	0
	10	r1										0	0	0
	11	r2											0	0
	12	vd1												0

В матрице H⁽³⁾ имеется единственный положительный элемент _6-11, расположенный на пересечении строки c₁ и столбца r₂. Переместить вершину c₁ из куска G₂ в кусок G₃, а вершину r₂ из – куска G₃ в кусок G₂. Разрезание графа после выполнения этой перестановки примет вид:

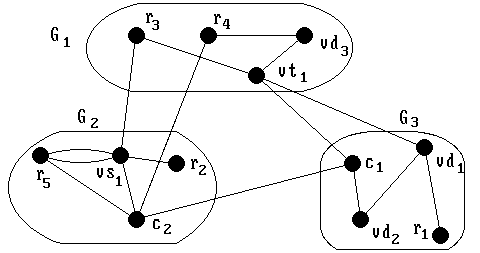
Рис. 7. Результат разрезания графа после перестановки вершин r₂ и c₁

Общее количество рёбер внутри полученных кусков L = 11, количество внешних связей между кусками K = 5. Коэффициент разрезания графа (G) = 11/5 = 2,2.

22) Переставить в матрице смежности R⁽³⁾ строки и столбцы r₂ и с₁. В результате матрица R⁽³⁾ примет вид:

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	r2	c2	vs1	vd2	r1	c1	vd1
	1	vd3	0	1	0	1	0	0	0	0	0	0	0	0
	2	vt1	1	0	1	0	0	0	0	0	0	0	1	1
	3	r3	0	1	0	0	0	0	0	1	0	0	0	0
	4	r4	1	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	1	2	0	0	0	0
R(4)=	6	r2	0	0	0	0	0	0	0	1	0	0	0	0	(30)
	7	c2	0	0	0	1	1	0	0	1	0	0	1	0
	8	vs1	0	0	1	0	2	1	1	0	0	0	0	0
	9	vd2	0	0	0	0	0	0	0	0	0	0	1	1
	10	r1	0	0	0	0	0	0	0	0	0	0	0	1
	11	c1	0	1	0	0	0	0	1	0	1	0	0	0
	12	vd1	0	1	0	0	0	0	0	0	1	1	0	0

23) Построить вспомогательную матрицу M⁽⁴⁾ по матрице смежности R⁽⁴⁾ и стандартной матрице F.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	r2	c2	vs1	vd2	r1	c1	vd1
	1	vd3	2	2	1	1	0	0	1	1	0	0	1	1
	2	vt1	2	2	1	1	0	0	1	1	0	0	1	1
	3	r3	2	2	1	1	0	0	1	1	0	0	1	1
	4	r4	2	2	1	1	0	0	1	1	0	0	1	1
	5	r5	0	0	1	1	3	1	2	4	0	0	1	0
M(4)=	6	r2	0	0	1	1	3	1	2	4	0	0	1	0	(31)
	7	c2	0	0	1	1	3	1	2	4	0	0	1	0
	8	vs1	0	0	1	1	3	1	2	4	0	0	1	0
	9	vd2	0	2	0	0	0	0	1	0	2	1	1	2
	10	r1	0	2	0	0	0	0	1	0	2	1	1	2
	11	c1	0	2	0	0	0	0	1	0	2	1	1	2
	12	vd1	0	2	0	0	0	0	1	0	2	1	1	2

24) По матрице смежности R⁽⁴⁾ и инверсии F стандартной матрицы F построить вспомогательную матрицу B⁽⁴⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	r2	c2	vs1	vd2	r1	c1	vd1
	1	vd3	0	0	0	0	0	0	0	0	0	0	0	0
	2	vt1	0	0	0	0	0	0	0	0	0	0	1	1
	3	r3	0	0	0	0	0	0	0	1	0	0	0	0
	4	r4	0	0	0	0	0	0	1	0	0	0	0	0
	5	r5	0	0	0	0	0	0	0	0	0	0	0	0
B(4)=	6	r2	0	0	0	0	0	0	0	0	0	0	0	0	(32)
	7	c2	0	0	0	1	0	0	0	0	0	0	1	0
	8	vs1	0	0	1	0	0	0	0	0	0	0	0	0
	9	vd2	0	0	0	0	0	0	0	0	0	0	0	0
	10	r1	0	0	0	0	0	0	0	0	0	0	0	0
	11	c1	0	1	0	0	0	0	1	0	0	0	0	0
	12	vd1	0	1	0	0	0	0	0	0	0	0	0	0

25) Построить вспомогательную матрицу P⁽⁴⁾ по матрицам M⁽⁴⁾ и B⁽⁴⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	r2	c2	vs1	vd2	r1	c1	vd1
	1	vd3	2	2	1	1	0	0	1	1	0	0	1	1
	2	vt1	2	2	1	1	0	0	1	1	0	0	0	0
	3	r3	2	2	1	1	0	0	1	0	0	0	1	1
	4	r4	2	2	1	1	0	0	0	1	0	0	1	1
	5	r5	0	0	1	1	3	1	2	4	0	0	1	0
P(4)=	6	r2	0	0	1	1	3	1	2	4	0	0	1	0	(33)
	7	c2	0	0	1	0	3	1	2	4	0	0	0	0
	8	vs1	0	0	0	1	3	1	2	4	0	0	1	0
	9	vd2	0	2	0	0	0	0	1	0	2	1	1	2
	10	r1	0	2	0	0	0	0	1	0	2	1	1	2
	11	c1	0	1	0	0	0	0	0	0	2	1	1	2
	12	vd1	0	1	0	0	0	0	1	0	2	1	1	2

26) Построить полуматрицу перестановочных коэффициентов H⁽⁴⁾.

			1	2	3	4	5	6	7	8	9	10	11	12
			vd3	vt1	r3	r4	r5	r2	c2	vs1	vd2	r1	c1	vd1
	1	vd3	0	0	0	0	-5	-3	-3	-5	-4	-3	-3	-3
	2	vt1		0	0	0	-5	-3	-3	-5	-2	-1	-2	-3
	3	r3			0	0	-3	-1	-1	-4	-3	-2	-1	-2
	4	r4				0	-3	-1	-3	-3	-5	-2	-1	-2
	5	r5					0	0	0	0	-5	-4	-3	-5
H(4)=	6	r2						0	0	0	-3	-2	-1	-3	(34)
	7	c2							0	0	-3	-2	-3	-3
	8	vs1								0	-6	-5	-4	-6
	9	vd2									0	0	0	0
	10	r1										0	0	0
	11	c1											0	0
	12	vd1												0

В полученной матрице H⁽⁴⁾ нет ни одного положительного коэффициента _ij. Это означает, что в матрице R⁽⁴⁾ не отыщется такой пары строк и столбцов, перестановка которых максимизировала бы функцию (1). Физически это означает, что в последнем полученном варианте разрезания графа (рис. 7) нет такой пары вершин, расположенных в разных кусках, перестановка которых привела бы к увеличению количества рёбер внутри кусков и тем самым к уменьшению количества внешних связей. Таким образом, разрезание графа, представленное на рис. 7, является окончательным и на этом процесс разрезания графа прекращается.

Граф, представленный на рис. 2, содержащий 12 вершин, разрезался на 3 куска по 4 вершины в каждом последовательным методом в практической работе № 3, итерационным методом с использованием чисел связности в практической работе № 4 и матричным методом в данной практической работе. В первом случае полученному разрезанию соответствовал коэффициент разбиения (G) = 1,29, во втором – (G) = 1,67 и самый высокий результат был достигнут при разрезании графа матричным методом – (G) = 2,2.

На рис. 8 представлен результат компоновки изделия РЭС, соответствующий полученному разрезанию графа принципиальной электрической схемы. Из рис. 8 видно, что полученное разрезание графа позволяет уменьшить количество связей между блоками изделия РЭС до четырёх. Связь конденсатора C1из первого блока с резисторами R2 и R5, конденсатором C2 и тиристором VS1 из второго блока (на рис. 8 показана пунктирной линией) устраняется за счёт соединения отрицательной обкладки конденсатора C1 с катодом стабилитрона VD2 внутри первого блока. Это позволяет минимизировать количество внешних контактов K*, посредством которых осуществляется физическое соединение первого блока со вторым. На практике это означает, что вместо четырёх внешних контактов первому блоку потребуется три (контакт, через который осуществляется связь, показанная пунктирной линией, является лишним). Уменьшение количества физических связей между блоками изделия РЭС по сравнению с количеством внешних связей между кусками разрезанного графа возможно не всегда и зависит в первую очередь от выбора вариантов покрывающих деревьев при развязке полных подграфов исходного графа принципиальной электрической схемы проектируемого изделия РЭС.

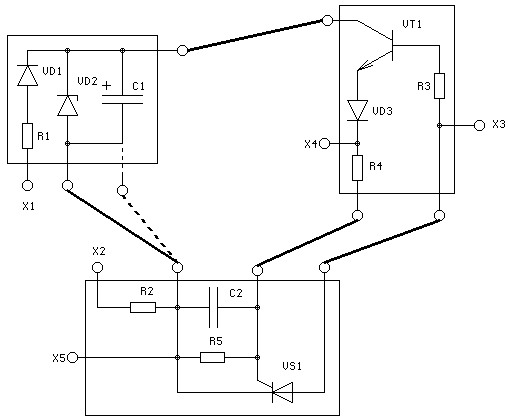
Рис. 8. Результат компоновки изделия РЭС