2 Комбинаторика

Сколько паролей можно создать, используя пять букв и два символа? Сколько времени понадобится компьютеру, чтобы взломать защиту другого компьютера? Сколькими способами можно расставить 25 человек для группового фото? В этом разделе мы рассмотрим методики подсчетов, которые позволяют давать ответы на такие вопросы.

Различные методики подсчетов будут использоваться нами при изучении курса теории вероятностей. В программировании элементарные методы подсчета – полезное средство для работы с задачами, в которых требуется перечислить все возможные состояния, рассматриваемые при выяснении корректности программы. Методы подсчета используются на разных этапах разработки корректной и эффективной программы.

2.1 Задача о коммивояжере

Задача о коммивояжере обманчива. Ее легко сформулировать, но очень трудно решить. Коммивояжер должен регулярно бывать в каждом из городов. Между каждой парой городов налажено регулярное воздушное сообщение. Задача состоит в том, чтобы составить такое расписание полетов, чтобы коммивояжер вернулся в тот же город, из которого отправился, побывав при этом ровно по одному разу во всех остальных городах, причем время в пути должно быть наименьшим.

Простейший (и не самый эффективный) алгоритм решения задачи состоит из трех шагов.

Шаг 1: Найти все возможные маршруты.

Шаг 2: Найти время в пути для всех маршрутов, найденных на первом шаге.

Шаг 3: Среди всех маршрутов найти тот, для которого время в пути минимально.

На следующем примере мы проследим за выполнением трех шагов этого алгоритма для множества из четырех городов.

Пример 2.1.1. Для четырех городов даны времена полета из одного города в другой. Найти наилучший маршрут для поездки по этим четырем городам. Число на пересечении строки и столбца – это время полета из города в город или из города в город . Ребра соединяют города, между которыми имеется воздушное сообщение. Число возле ребра – продолжительность полета между двумя городами – концам ребра.

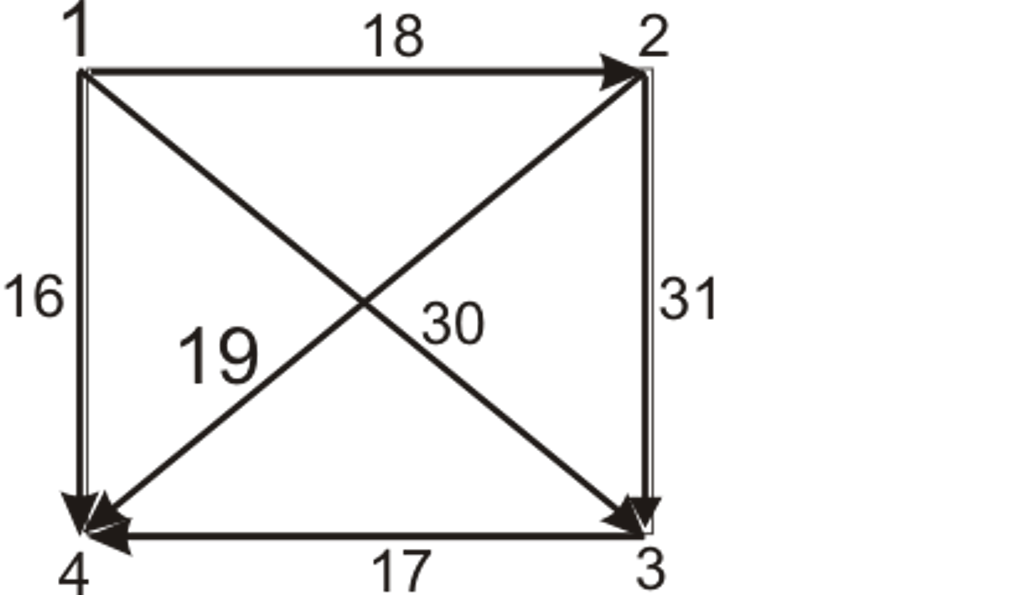
Решение.

Шаг 1: выпишем все возможные маршруты:

1-2-3-4-1

1-2-4-3-1

1-3-2-4-1

1-4-3-2-1

1-3-4-2-1

1-4-2-3-1

Шаг 2: вычислим время в пути для каждого маршрута:

1-2-3-4-1:18+31+17+16=82

1-2-4-3-1:18+19+17+30=84

1-3-2-4-1:30+31+19+16=96

1-4-3-2-1:16+17+31+18=82

1-3-4-2-1:30+17+19+18=84

1-4-2-3-1:16+19+31+30=96

Шаг 3: выберем кратчайший маршрут:

1-2-3-4-1:18+31+17+16=82.

В этом параграфе мы обратимся к задачам пересчета, чьи решения получаются с помощью двух правил: правил суммы и правило произведения.

Общие задачи пересчета связаны с выборкой некоторого числа элементов из заданного множества. Такие задачи можно разделить на типы в зависимости от того, как выбираются элементы: с повторением или без повторений, с учетом порядка выбора или без учета. Ниже мы выведем формулы для каждого из перечисленных типов задач.

В дальнейшем мы займемся эффективностью алгоритмов. Это одно из приложений комбинаторики к проблемам информатики.