Завдання 4. Задача оптимального розподілу ресурсів
1. Постановка задачі
Розглянемо приклад. Деяка установа надає послуги виду 1 та виду 2. Кожна послуга виду 1 дає прибуток 60 грн., а на її надання витрачається 1 одиниця ресурсу 1, 0.5 одиниць ресурсу 2 і 1 одна одиниця ресурсу 3. Кожна послуга виду 2 дає прибуток 160 грн., а на її надання витрачається 2 одиниці ресурсу 1, 0.4 одиниці ресурсу 2 і 4 одиниці ресурсу 3. Ресурси установи обмежені: щотижня вона може отримувати від своїх постачальників 130 одиниць ресурсу 1, 50 одиниць ресурсу 2 і 220 одиниць ресурсу 3. Наведені дані зафіксуємо у таблиці.
Послуги |
Ресурс 1 |
Ресурс 2 |
Ресурс 3 |
Прибуток |
Вид 1 |
1 |
0.5 |
1 |
60 |
Вид 2 |
2 |
0.4 |
4 |
160 |
Ресурси |
130 |
50 |
220 |
|
Треба визначити, в якій кількості спланувати надання послуг виду 1 і виду 2, щоб прибуток був максимальним.
Подібні задачі називаються задачами лінійного програмування. Вони призначені для оптимального розподілу ресурсів, тобто для найбільш економічно ефективного використання цих ресурсів з урахуванням обмеженого їх обсягу.
Сформулюємо
задачу математично. Позначимо через
і
заплановану до надання кількість послуг
1 і послуг 2 відповідно. Обмеженість
ресурсів фірми означає, що мають
задовольнятись такі нерівності:
.
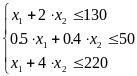Крім того, за змістом задачі її змінні
мають бути невід’ємними, тобто:
і
.
Вони також мають бути цілочисельними.
Прибуток від запланованих до виробництва
стільців та крісел визначається за
формулою
.
Отже, оптимальний план фірми, тобто
числа
і
мають бути такими, щоб задовольнялись
всі наведені нерівності, а прибуток F
досягав максимального значення.
Один
із допустимих планів цієї задачі такий:
і
.
При цьому:
,
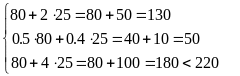тобто ресурсу 3 вистачає із запасом, а
ресурси 1 і 2 використовуються повністю.
Прибуток при цьому складає
грн. Указаний план є допустимим, але він
не є оптимальним. Дійсно, для іншого
плану
і
отримуємо:
.
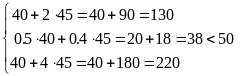При цьому ресурсу 2 вистачає із запасом,
ресурси 1 і 3 використовуються повністю,
а прибуток складає
грн., що суттєво краще у порівнянні з
попереднім.
Отже, розв’язок задачі розподілу ресурсів має багатоваріантний характер.
2. Розв’язування задачі засобами Excel
В MS Excel для розв’язування задач лінійного програмування може використовуватись спеціальна надбудова, яка має назву Поиск решения.
Порядок розв’язування задачі лінійного програмування:
Установити надбудову Поиск решения. Для цього виконати команду Сервис-Надстройки.... Внаслідок цього з’являється вікно Надстройки. В цьому вікні у прокручуваному списку Список надстроек: слід установити прапорець на пункті Поиск решения і натиснути кнопку OK.
В робочому листі Excel створити наступну форму:
A
B
1
Змінні:
2
x1 =
3
x2 =
4
5
Максимальне значення:
6
7
Обмеження:
8
№1:
9
№2:
10
№3:
В комірки B8, B9 і B10 внести такі формули: “=B2+2*B3”, “=0.5*B2+0.4*B3”, “=B2+4*B3”.
В комірку B5 внести формулу цільової функції: «=60*B2+160*B3».
Звернутися до надбудови Поиск решения з метою розв’язування задачі. Для цього виконати команду Сервис-Поиск решения.... Після цього на екрані з’являється вікно Поиск решения, в яке здійснюється внесення задачі лінійного програмування.
В полі Установить целевую ячеку: надрукувати $B$5.
Установити відмітку на пункті Равной: Максимальному значению.
В полі Изменяя ячейки: надрукувати $B$2:$B$3.
Ввести перше обмеження. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$8, в полі Ограничение: вибрати значок “<=” і надрукувати значення 130. Натиснути кнопку ОК.
Аналогічно ввести друге і третє обмеження.
Ввести умови невід’ємності змінних. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$2:$B$3, в полі Ограничение: вибрати значок «>=» і надрукувати значення 0. Натиснути кнопку OK.
Ввести умови цілочисельності змінних. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$2:$B$3, в полі Ограничение: вибрати пункт цел. Натиснути кнопку OK.
Натиснути кнопку Параметри..., установити відмітку на пункті Линейная модель і натиснути кнопку OK.
Задачу ЛП повністю підготовлено. Натиснути у вікні Поиск решения кнопку Выполнить.
З’являється вікно Результаты поиска решения, в якому повідомляється, що Решение найдено. Відмітити пункт Сохранить найденное решение і натиснути кнопку OK. На листі електронної таблиці бачимо оптимальний план.