2Розрахунок сферичного крана

2.1 Геометричний розрахунок сферичного крана

На рисунку 2.1 показана пробка сферичного крана[1].

Рисунок 2.1 – Схема ущільнювальної поверхні у

сферичному крані

Вікно проходу сферичного крана виконують у вигляді круглого циліндричного отвору. Унайпростішому варіанті сферичного крана пробка виготовляється у вигляді сфери і знаходиться між двома ущільнювальними кільцями. Герметичність затвора залежить від ширини кільця L (рисунок 2.2), яка аналогічна перекриттю у конічних кранах [1].

1 – корпус; 2 - пробка

Рисунок 3.2 – Схематичний переріз сферичного крана

Діаметр проходу (вікна) крана в корпусі визначаємо за формулою

(2.1)

де f- коефіцієнт повно прохідності;

DN – діаметр умовного проходу пробки крана, мм.

Підставляємо числові значення у формулу (2.1)

Орієнтовне значення перекриття (ширини ущільнювального кільця) у сферичних кранах при проведенні проектних розрахунків визначаємо за формулою [1]

(2.2)

де n - величина перекриття, мм;

k_у – коефіцієнт, який визначається в залежності від матеріалу ущільнювальних кілець ;

DN – умовний діаметр, мм;

PN – умовний тиск, кгс/см².

Згідно з таблицею 3.1 [1, с. 35], для сталі коефіцієнтk_у=0,25.

Підставляємо числові значення у формулу (2.2)

Діаметр сферичної пробки визначаємо, як і для конічної пробки, за формулою (1.8) при умові, що = D, тобто

, (2.3)

Оскільки центральний кут, який відповідний перекриттю n

,

то

, (2.4)

Центральний кут зовнішнього краю ущільнювального кільця визначаємо за формулою

, (2.5)

Центральний кут внутрішнього краю ущільнювального кільця визначаємо за формулою

, (2.6)

2.2 Силовий розрахунок сферичного крана

Зусилля від тиску робочого середовища на пробку сферичного крана визначаємо за формулою:

, (2.7)

де - радіус середньої лінії ущільнювального кільця;

- робочий тиск середовища, ;

Виходячи із конструктивних міркувань, приймають, що , а тому[1]

, (2.8)

де ,

.

Підставляємо числові значення у формули (2.7), (2.8)

Якщо припустити, що тиск середовища проникає до середини ущільнення, то крутячий момент, для кранів без попереднього затягування і при затягуванні зусиллям, визначаємо за такими формулами [1]

; (2.9)

, (2.10)

де - зусилля попереднього затягування ущільнювальних кілець, кгс;

– коефіцієнт тертя між пробкою і матеріалом ущільнення;

Згідно таблиці 3.2 [1, с. 37], коефіцієнт = 0,1.

Підставляємо числові значення у формули (2.9), (2.10)

Клиновий ефект у сферичному крані також не відіграє суттєвої ролі через великий кут, який утворюють ущільнювальні поверхні (біля 90⁰). У зв’язку із цим питомий тиск, який необхідний для забезпечення герметичності сферичних і циліндричних кранів без змащування визначаємо за формулою[1]

, (2.11)

де – коефіцієнт, який залежить від типу робочого середовища;

с і – сталі, які залежать від матеріалу ущільнення;

n – ширина перекриття (ущільнення), см.

Коефіцієнти , с і прийняті у розділі 1.

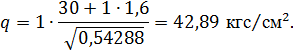
Середній питомий тиск на вихідному кільці, за умови, що ,визначаємо за формулою

, (2.12)

де – коефіцієнт, який залежить від кутової ширини ущільнювального кільця, = 4,11 -розраховано за допомогою інтерполяції за даними таблиці 3.5[1].

Підставляємо числові значення у формулу (2.12)

Максимальний питомий тиск , який буде на внутрішньому краю вихідного кільця крана без попереднього затягування і при затягуванні зусиллям, яке , визначається за формулою

, (2.13)

Якщо у формулі (2.7) врахувати формулу (2.8), то отримаємо формулу для визначення зусилля від дії тиску робочого середовища на пробку сферичного крана [1]

, (2.14)

Виходячи із умови, що момент тертя у сальнику і у опорі пробки не перевищують 30 % від моменту тертя пробки об корпус, орієнтовний розрахунковий крутячий момент на шпинделі приймається рівним [1]

, (2.15)

Діаметр шпинделя (суцільного хвостовика пробки) у сальнику при проектному розрахунку визначається із умови кручення за формулою

, (2.16)

де - розрахункове допустиме напруження.

Для стальних деталей за номінальне допустиме напруження приймається менше із двох значень [1]

; (2.17)

, (2.18)

де - тимчасовий опір розриву (межа міцності) ;

- межа плинності.

Обираємо сталь 15Х з межею міцності межа плинності .

Підставляємо числові значення у формули (2.17), (2.18)

Вибираємо мінімальне допустиме напруження .

Підставляємо числові значення у формулу (2.16)

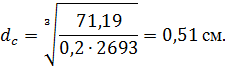
Схематично сальник крана із змащуванням показано на рисунку 2.3[1].

1 - канавка із набивкою; 2 – шпиндель; 3 – лубрикатор;

4 – порожнина для мастила

Рисунок 2.3 – Схематичне зображення сальника крана з плаваючою пробкою із змащуванням

Момент тертя у різі (у тому числі і в сальнику) при повороті шпинделя визначаєvj за формулою

, (2.19)

де _ср.р - середній діаметр різі;

- кут підйому різі;

- кут тертя;

Значення коефіцієнта тертя у різі приймаємо Тоді

, (2.20)

Кут підйому різі визначаємо із формули

, (2.21)

де - крок різі.

Розміри різі шпинделя приймаємо із конструктивних міркувань.Середній діаметр різі _ср.р = 100 мм , крок різі

Підставляємо числові значення у формулу (2.19)

Крутячий момент, який необхідно для повороту пробки крана

, (2.22)

.

28