Вариант 6

ЗАДАЧА 1

Дискретная случайная величина Х задана законом распределения:

А) Построить многоугольник распределения

Б) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение

В) Найти функцию распределения F(X) и построить ее график

ЗАДАЧА 2

Учебник издан тиражом 300 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,00003. Найти вероятность того, что тираж содержит не более трех бракованных книг.

ЗАДАЧА 3

Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=2X+5Y, если M(X)=3, M(Y)=6, D(X)=4, D(Y)=2.

ЗАДАЧА 4

Задана плотность распределения непрерывной случайной величины Х

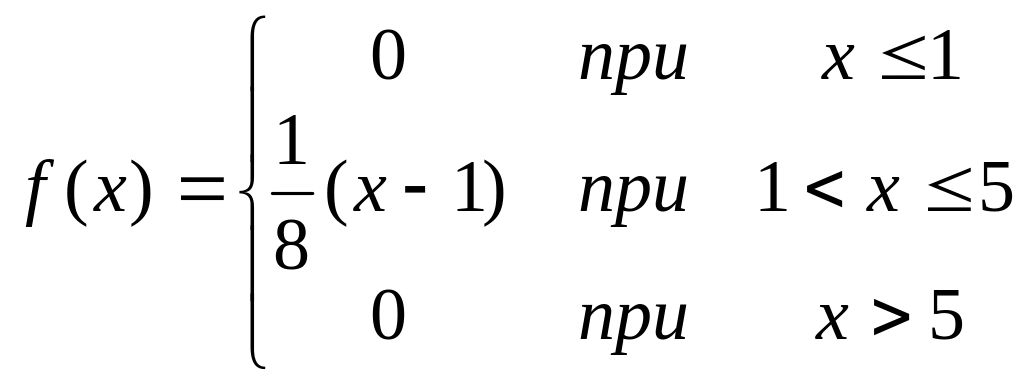
А) Найти функцию распределения F(x)

Б) Построить графики функций F(x) и f(x)

В) Найти математическое ожидание и дисперсию для этой случайной величины.

ЗАДАЧА 5

Случайные ошибки измерения Х подчинены нормальному закону распределения со средним квадратическим отклонением мм и математическим ожиданием а=0. Найти вероятность того, что измерение будет произведено с ошибкой, не превышающей по величине 10 мм.

ЗАДАЧА 6

По данному распределению выборки объема п=25

найти выборочную среднюю , выборочную дисперсию , исправленную выборочную дисперсию .

Указание. Перейти к условным вариантам.

Вариант 7

ЗАДАЧА 1

Дискретная случайная величина Х задана законом распределения:

А) Построить многоугольник распределения

Б) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение

В) Найти функцию распределения F(X) и построить ее график

ЗАДАЧА 2

Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,7. Стрелку выдают патроны, пока он не промахнется. Составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку. Найти вероятность того, что стрелку выдадут не более 4 патронов.

ЗАДАЧА 3

Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=7X+5Y, если M(X)=3, M(Y)=4, D(X)=3, D(Y)=2.

ЗАДАЧА 4

Задана плотность распределения непрерывной случайной величины Х

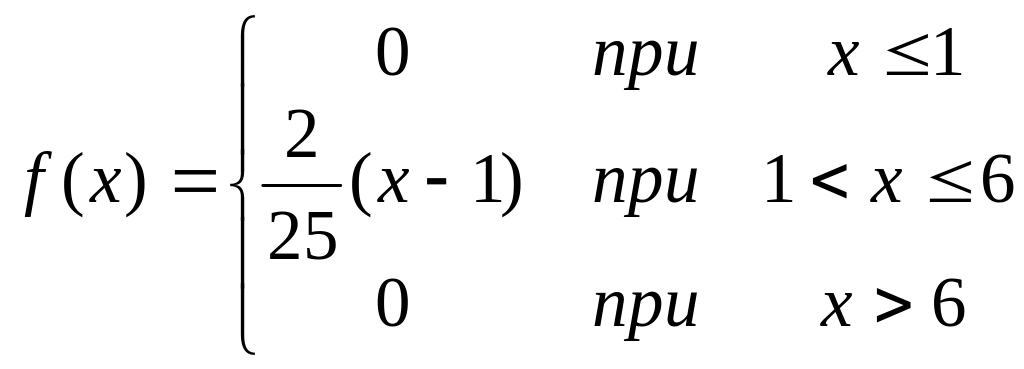
А) Найти функцию распределения F(x)

Б) Построить графики функций F(x) и f(x)

В) Найти математическое ожидание и дисперсию для этой случайной величины.

ЗАДАЧА 5

Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятности . Найти вероятность того, что в результате испытания Х попадает в интервал (0,5; 0,8)

ЗАДАЧА 6

По данному распределению выборки объема п=50

найти выборочную среднюю , выборочную дисперсию , исправленную выборочную дисперсию .

Указание. Перейти к условным вариантам.

Вариант 8

ЗАДАЧА 1

Дискретная случайная величина Х задана законом распределения:

А) Построить многоугольник распределения

Б) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение

В) Найти функцию распределения F(X) и построить ее график

ЗАДАЧА 2

Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,6. Стрелку выдают патроны, пока он не промахнется. Составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку. Найти вероятность того, что стрелку выдадут не более 5 патронов.

ЗАДАЧА 3

Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=2X+6Y, если M(X)=3, M(Y)=5, D(X)=4, D(Y)=2.

ЗАДАЧА 4

Задана плотность распределения непрерывной случайной величины Х

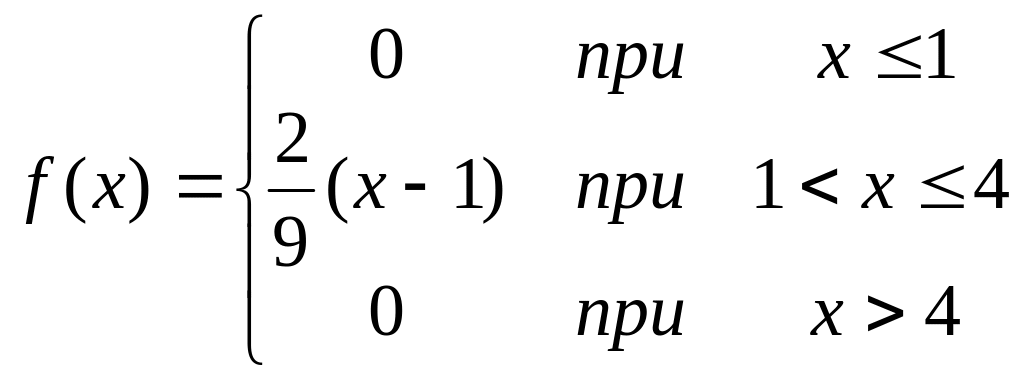
А) Найти функцию распределения F(x)

Б) Построить графики функций F(x) и f(x)

В) Найти математическое ожидание и дисперсию для этой случайной величины.

ЗАДАЧА 5

Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятности . Найти вероятность того, что в результате испытания Х попадает в интервал (2,5)

ЗАДАЧА 6

По данному распределению выборки объема п=100

найти выборочную среднюю , выборочную дисперсию , исправленную выборочную дисперсию .

Указание. Перейти к условным вариантам.