
Домашняя контрольная работа № 2 по теории вероятностей. Контрольную нужно сдать в понедельник, 3 декабря.
|
22 гр ПИ ИПОИТ |
вари ант |
1 |
Абрамова |
1 |
2 |
Бербега |
2 |
3 |
Буранбаева |
3 |
4 |
Гудкова |
4 |
5 |
Исмагилов |
5 |
6 |
Кайбышева |
6 |
7 |
Камалов |
7 |
8 |
Кидрасова |
8 |
9 |
Косинцева К |
1 |
10 |
Косинцева Э |
2 |
11 |
Кутлугильдин |
3 |
12 |
Латыпов |
4 |
13 |
Лукманова |
5 |
14 |
Матвеева |
6 |
15 |
Муфтахова |
7 |
16 |
Пономарева |
8 |
17 |
Рафиков |
1 |
18 |
Святкин |
2 |
19 |
Слюсарев |
3 |
20 |
Старцев |
4 |
21 |
Хажиев |
5 |
22 |
Харисов |
6 |
23 |
Хемраев |
7 |
24 |
Хурматуллина |
8 |
25 |
Якупова |
1 |
26 |
Яруллина |
2 |
|
|
|
Вариант 1
ЗАДАЧА 1
Дискретная случайная величина Х задана законом распределения:
![]()
А) Построить многоугольник распределения
Б) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение
В) Найти функцию распределения F(X) и построить ее график
ЗАДАЧА 2
В партии 15% нестандартных деталей. Наудачу отобраны 3 детали. Написать биномиальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди отобранных.
Для полученного закона распределения найти математическое ожидание и дисперсию.
ЗАДАЧА 3
Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=2X+5Y, если M(X)=3, M(Y)=1, D(X)=2, D(Y)=4.
ЗАДАЧА 4
Задана плотность распределения непрерывной случайной величины Х
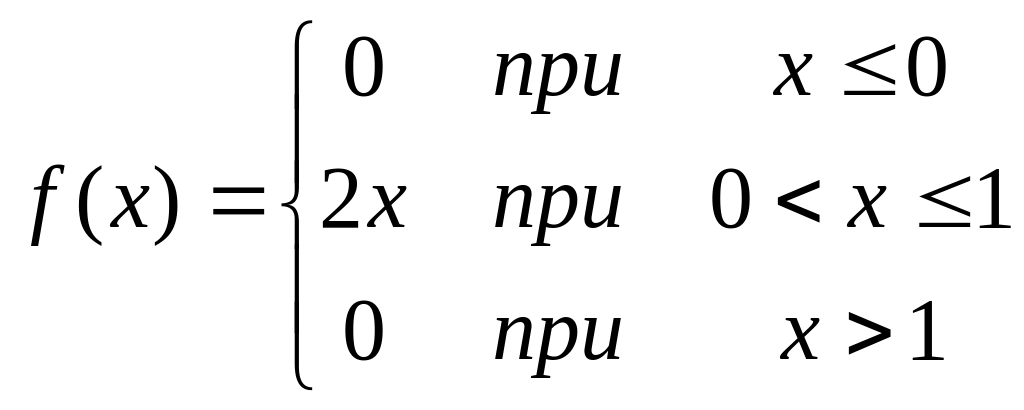
А) Найти функцию распределения F(x)
Б) Построить графики функций F(x) и f(x)
В) Найти математическое ожидание и дисперсию для этой случайной величины.
ЗАДАЧА 5
Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 25 и 3. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (20,30)
ЗАДАЧА 6
По данному распределению выборки объема п=100
![]()
найти выборочную
среднюю
![]() ,
выборочную дисперсию
,
выборочную дисперсию
![]() ,
исправленную выборочную дисперсию
,
исправленную выборочную дисперсию
![]() .
.
Указание. Перейти к условным вариантам.
Вариант 2
ЗАДАЧА 1
Дискретная случайная величина Х задана законом распределения:
![]()
А) Построить многоугольник распределения
Б) Найти математическое ожидание, дисперсию, среднее квадратическое отклонение
В) Найти функцию распределения F(X) и построить ее график
ЗАДАЧА 2
В партии 20% нестандартных деталей. Наудачу отобраны 4 детали. Написать биномиальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди отобранных.
ЗАДАЧА 3
Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайной величины Z=3X+2Y, если M(X)=2, M(Y)=3, D(X)=4, D(Y)=5.
ЗАДАЧА 4
Задана плотность распределения непрерывной случайной величины Х
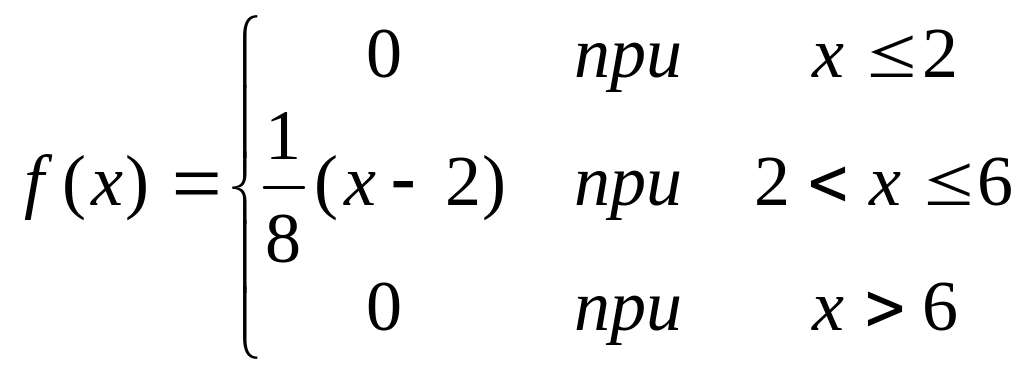
А) Найти функцию распределения F(x)
Б) Построить графики функций F(x) и f(x)
В) Найти математическое ожидание и дисперсию для этой случайной величины.
ЗАДАЧА 5
Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 15 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (10,30)
ЗАДАЧА 6
По данному распределению выборки объема п=100
![]()
найти выборочную среднюю , выборочную дисперсию , исправленную выборочную дисперсию .
Указание. Перейти к условным вариантам.
