
- •Математика
- •Общие указания по подготовке к фэпо
- •Основная литература
- •Дополнительная литература
- •Электронные ресурсы
- •Раздел 1. Алгебра и геометрия
- •1. Определители
- •2. Матрицы
- •3. Векторная алгебра
- •Раздел 2. Математический анализ
- •Раздел 3. Дифференциальные уравнения
- •Раздел 4. Теория функций комплексного переменного.
- •Раздел 5. Теория вероятностей.
- •Раздел 6. Численные методы
- •2.Графический способ
- •1 Численные методы решения алгебраических уравнений
- •Раздел 7. Дискретная математика и абстрактная алгебра
- •664074, Иркутск, Лермонтова, 83
Раздел 4. Теория функций комплексного переменного.
Формы записи комплексного числа.
Операции над комплексными числами.
Определение функции комплексного переменного.
Дифференцирование функций комплексного переменного.
Периодические функции.
Элементы гармонического анализа.
Ряд Фурье. Теорема Дирихле.
Алгебраическая форма:
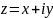
где
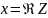 - действительная часть комплексного
числа
- действительная часть комплексного
числа
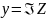 -
мнимая часть комплексного числа.
-
мнимая часть комплексного числа.
 )
)
Тригонометрическая
форма: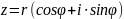
Показательная
форма:

где
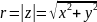 - модуль комплексного числа z.
- модуль комплексного числа z.
 -
главное значение аргумента комплексного
числа z.
-
главное значение аргумента комплексного
числа z.
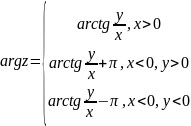
Дополнительные
формулы для вычисления
 :
:
Операции над комплексными числами.

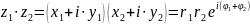
 -
необходимо умножить числитель и
знаменатель на число сопряженное
знаменателю. Если
,
то
-
необходимо умножить числитель и
знаменатель на число сопряженное
знаменателю. Если
,
то
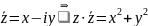 .
.
Деление
комплексных чисел в показательной
форме:
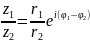 .
.
 -
формула Муавра.
-
формула Муавра.

 ,
где
,
где

 -
уравнение
окружности с центром в точке
-
уравнение
окружности с центром в точке
 и радиусом
и радиусом .
.
Функции комплексного переменного.



Основные элементарные функции:
 -
показательная функция.
-
показательная функция.
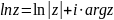 -
логарифмическая
функция.
-
логарифмическая
функция.


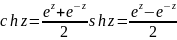
 -
формула
Эйлера.
-
формула
Эйлера.
Дифференцирование функций комплексного переменного.

Условие
Коши-Римана (дифференцируемости
функции
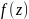 )
)
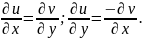
Для функций комплексного переменного справедливы правила дифференцирования функций действительного переменного.
Периодические функции.
 имеют
период
имеют
период
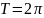 .
.
 имеют
период
имеют
период
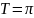 .
.
Если
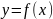 - периодическая функция с периодом
- периодическая функция с периодом
 ,
то
,
то
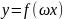 является периодической с периодом
является периодической с периодом
 .
.
Простые гармонические колебания.
 или
или
 ,
где
,
где
 -
амплитуда колебаний
-
амплитуда колебаний
 -
частота колебаний
-
частота колебаний
- начальная фаза колебаний.
Разложение в ряд Фурье.
На произвольном интервале
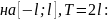

где
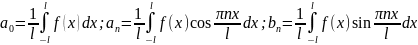 .
.
Для
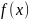 - четной:
- четной:
 ,
,
где

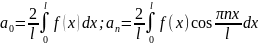 .
.
Для
- нечетной:
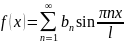 ,
,
где

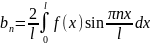 .
.
На интервале
 при
:
при
:
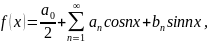
где
 .
.
Для
- четной:
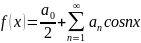 ,
,
где
 .
.
Для
- нечетной:
 ,
,
где
 .
.
Условия, при которых функцию можно представить в виде ряда Фурье на
 :
:
Теорема Дирихле: Пусть на удовлетворяет двум условиям:
- кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва первого рода.
- кусочно-монотонна, т.е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число монотонных интервалов.
Тогда соответствующий функции ряд Фурье сходится на этом отрезке и при этом:
В точках непрерывности функции сумма ряда
 совпадает с самой функцией:
совпадает с самой функцией:
 .
.В каждой точке
 разрыва функции сумма ряда равна:
разрыва функции сумма ряда равна:
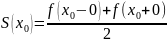 ,
т.е. равна среднему арифметическому
пределов функции
справа и слева.
,
т.е. равна среднему арифметическому
пределов функции
справа и слева.В точках
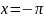 и
и
 (на концах отрезка) сумма ряда равна:
(на концах отрезка) сумма ряда равна:
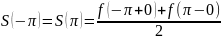 .
.
Контрольные задания к разделу №4
1 |
Формы записи комплексного числа |
||||||
1.1 |
Условие |
Варианты |
|||||
Записать
комплексное число
|
|
||||||
Решение Т.к.
|
|||||||
1.2 |
Условие |
Варианты |
|||||
Модуль комплексного числа (-2-5i) равен:
|
|
||||||
Решение
|
|||||||
1.3 |
Условие |
Варианты |
|||||
Мнимая
часть комплексного числа
|
|
||||||
Решение
|
|||||||
1.4 |
Условие |
Варианты |
|||||
Аргумент
комплексного числа
|
|
||||||
Решение
|
|||||||
1.5 |
Условие |
Варианты |
|||||
Действительная часть комплексного числа равна:
|
|
||||||
Решение
|
|||||||
1.6 |
Условие |
Варианты |
|||||
|
|
||||||
Решение
|
|||||||
1.7 |
Условие |
Варианты |
|||||
Комплексное число можно представить в виде (выбрать несколько ответов): |
|
||||||
Решение
(б)
(г) |
|||||||
1.8 |
Условие |
Варианты |
|||||
Комплексное
число
|
|
||||||
Решение
|
|||||||
1.9 |
Условие |
Варианты |
|||||
Н |
а)
б)
в)
г)
|
||||||
Решение
|
|||||||
1.10 |
Условие |
Варианты |
|||||
Укажите соответствие между областями и их геометрическими интерпретациями:
|
а)
б) в) г)
д) |
||||||
Решение 1)
3)
|
|||||||
1.11 |
Условие |
Варианты |
|||||
Если
z
комплексное число,
|
|
||||||
Решение
|
|||||||
1.12 |
Условие |
Варианты |
|||||
Установите соответствие между комплексным числом и его модулем: 1)
3)
|
а) 5; б) 13; в) 3; г) 1; д) 2; е)
|
||||||
Решение 1)
2)
3)
4)
|
|||||||
1.13 |
Условие |
Варианты |
|||||
Аргумент
комплексного числа
|
|
||||||
Решение
|
|||||||
1.14 |
Условие |
Варианты |
|||||
Н
|
|
||||||
Решение
|
|||||||
1.15 |
Условие |
Варианты |
|||||
Если
,
то множество точек комплексной
плоскости, заданных условием
|
а)
б)
в)
г)
|
||||||
Решение:
|
|||||||
1.16 |
Условие |
Варианты |
|||||
Расположить комплексные числа в порядке возрастания модулей:
|
|
||||||
Решение
Таким
образом,
|
|||||||
2 |
Операции над комплексными числами |
||||||
2.1 |
Условие |
Варианты |
|||||
Найти
значение выражения
|
|
||||||
Решение Умножим и числитель, и знаменатель данного дробного выражения на сопряженное знаменателю. Имеем
|
|||||||
2.2 |
Условие |
Варианты |
|||||
Даны комплексные числа
Тогда
|
|
||||||
Решение
|
|||||||
2.3 |
Условие |
Варианты |
|||||
Дано:
|
|
||||||
Решение
|
|||||||
2.4 |
Условие |
Варианты |
|||||
Если
и
|
|
||||||
Решение
|
|||||||
2.5 |
Условие |
Варианты |
|||||
Дано
комплексное число
|
|
||||||
Решение
|
|||||||
2.6 |
Условие |
Варианты |
|||||
Пусть
|
|
||||||
Решение Используя
равенство
Имеем
|
|||||||
2.7 |
Условие |
Варианты |
|||||
Результатом
деления комплексного числа
|
|
||||||
Решение
|
|||||||
2.8 |
Условие |
Варианты |
|||||
Сумма
комплексных чисел
|
|
||||||
Решение
|
|||||||
2.9 |
Условие |
Варианты |
|||||
Даны
два комплексных числа
|
а) 32 б) 12 в) 8 г) 20 |
||||||
Решение
|
|||||||
2.10 |
Условие |
Варианты |
|||||
Даны
два комплексных числа
Тогда
аргумент частного
|
|
||||||
Решение
|
|||||||
2.11 |
Условие |
Варианты |
|||||
Частное
|
|
||||||
Решение
|
|||||||
2.12 |
Условие |
Варианты |
|||||
Частное
от деления комплексного числа
|
|
||||||
Решение
|
|||||||
2.13 |
Условие |
Варианты |
|||||
Найти
значение выражения
|
|
||||||
Решение
|
|||||||
2.14 |
Условие |
Варианты |
|||||
Одним
из корней
|
|
||||||
Решение Таким образом, верный ответ а). |
|||||||
2.15 |
Условие |
Варианты |
|||||
Дано
комплексное число
|
|
||||||
Решение
|
|||||||
3 |
Определение функции комплексного переменного |
||||||
3.1 |
Условие |
Варианты |
|||||
Дана
функция
|
|
||||||
Решение Найдем
значение функции
|
|||||||
3.2 |
Условие |
Варианты |
|||||
Значение
функции
|
|
||||||
Решение
|
|||||||
3.3 |
Условие |
Варианты |
|||||
Мнимая
часть функции
|
|
||||||
Решение
|
|||||||
3.4 |
Условие |
Варианты |
|||||
Значение
функции
|
|
||||||
Решение
|
|||||||
3.5 |
Условие |
Варианты |
|||||
Установите
соответствие между функцией комплексного
переменного и ее значением в точке
1)
|
|
||||||
Решение 1)
2)
3)
|
|||||||
3.6 |
Условие |
Варианты |
|||||
Значения
функции
|
|
||||||
Решение
|
|||||||
3.7 |
Условие |
Варианты |
|||||
Значение
функции
|
|
||||||
Решение
|
|||||||
4 |
Дифференцирование функции комплексного переменного |
||||||
4.1 |
Условие |
Варианты |
|||||
Если
|
|
||||||
Решение
,
|
|||||||
4.2 |
Условие |
Варианты |
|||||
Если
и
|
|
||||||
Решение
|
|||||||
4.3 |
Условие |
Варианты |
|||||
Значение
производной функции
|
|
||||||
Решение
|
|||||||
4.4 |
Условие |
Варианты |
|||||
Если
|
|
||||||
Решение
|
|||||||
4.5 |
Условие |
Варианты |
|||||
Если
|
|
||||||
Решение
.
|
|||||||
5 |
Периодические функции |
||||||
5.1 |
Условие |
Варианты |
|||||
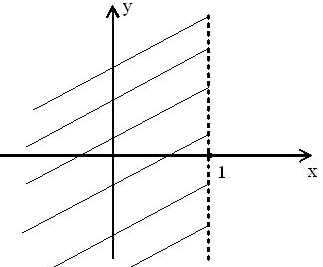
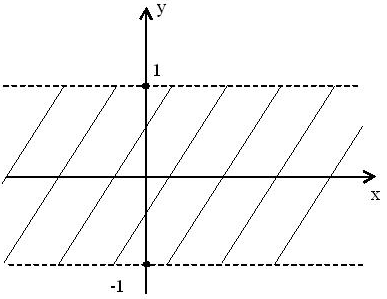
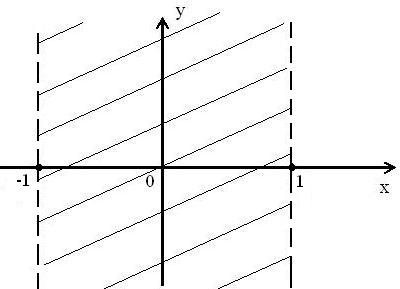
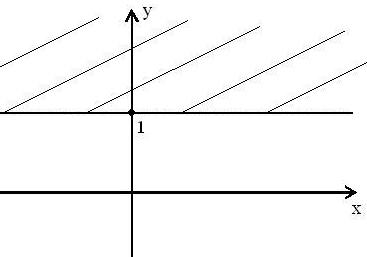
Укажите график периодической функции из приведенных ниже. 1) 3)
|
|
||||||
Решение Графиком периодической функции является вариант 2. |
|||||||
5.2 |
Условие |
Варианты |
|||||
Произведение
значений параметра
|
|
||||||
Решение Воспользуемся
тем, что если
периодическая функция с периодом Т,
то
функция
Таким
образом, ответом является число
|
|||||||
5.3 |
Условие |
Варианты |
|||||
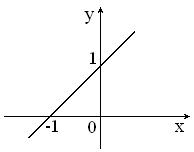
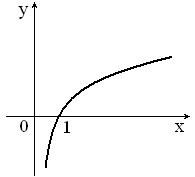
Указать две периодические функции с периодом 2 из представленных ниже: 1)
3)
|
|
||||||
Решение
Если
периодическая функция с периодом Т,
то
функция
является периодической с периодом
.
Тогда для
|
|||||||
5.4 |
Условие |
Варианты |
|||||
Произведение
значений параметра а,
при которых период функции
|
|
||||||
Решение Воспользуемся
тем, что если
периодическая функция с периодом Т,
то
функция
является периодической с периодом
.
Функция
Таким
образом,
|
|||||||
5.5 |
Условие |
Варианты |
|||||
Установить соответствие между периодической функцией и значением ее периода: 1)
3)
|
|
||||||
Решение
Если
периодическая функция с периодом Т,
то
функция
является периодической с периодом
.
Тогда для
,
отсюда
|
|||||||
6 |
Элементы гармонического анализа |
||||||
6.1 |
Условие |
Варианты |
|||||
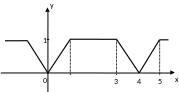
На
рисунке изображен график периодической
функции
.
Ее аналитическое представление на
отрезке
|
|
||||||
Решение
При
|
|||||||
6.2 |
Условие |
Варианты |
|||||
Гармонические колебания с амплитудой А, частотой ω и начальной фазой φ описываются законом … |
|
||||||
Решение Гармоническое колебательное движение описывает функция . |
|||||||
6.3 |
Условие |
Варианты |
|||||
Если
функция
|
|
||||||
Решение: Величина ω – частота колебания. |
|||||||
6.4 |
Условие |
Варианты |
|||||
Если функция описывает гармоническое колебательное движение, то начальной фазой колебания называется величина … |
|
||||||
Решение: Величина φ – начальная фаза колебания. |
|||||||
6.5 |
Условие |
Варианты |
|||||
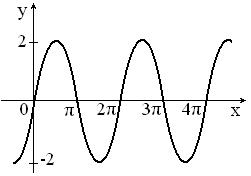
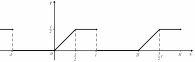
На
рисунке изображен график периодической
функции
.
Ее аналитическое представление на
промежутке
|
|
||||||
|
|
||||||
Решение
При
|
|||||||
7 |
Ряд Фурье. Теорема Дирихле |
||||||
7.1 |
Условие |
Варианты |
|||||
Коэффициент
|
|
||||||
Решение Данная
функция непрерывна на всей числовой
прямой и имеет кусочно-непрерывную
производную,
периодическая. Следовательно, ее ряд
Фурье сходится к ней в каждой точке
|
|||||||
7.2 |
Условие |
Варианты |
|||||
График
функции
при
Тогда ряд Фурье для этой функции имеет вид … |
а)
б)
в)
г)
|
||||||
Решение Функция не является ни четной, ни нечетной, следовательно, ответ 1). |
|||||||
7.3 |
Условие |
Варианты |
|||||
Функция
,
заданная на
|
а)
б)
в)
г)
|
||||||
Решение Если
функция на отрезке
четная, то коэффициент
|
|||||||
7.4 |
Условие |
Варианты |
|||||
Дана
функция
|
|
||||||
Решение нечетная функция
|
|||||||
7.5 |
Условие |
Варианты |
|||||
Дана
функция
|
|
||||||
Решение
|
|||||||
7.6 |
Условие |
Варианты |
|||||
Коэффициент
|
|
||||||
Решение Функция
|
|||||||
7.7 |
Условие |
Варианты |
|||||
Коэффициент
ряда Фурье периодической функции
с периодом 2l,
заданный на интервале
|
|
||||||
Решение Данная
функция кусочно-гладкая, причем
|
|||||||
7.8 |
Условие |
Варианты |
|||||
Найти
сумму ряда в точке
|
|
||||||
Решение По
теореме Дирихле в каждой точке
разрыва функции сумма ряда равна
,
т.е. среднему арифметическому
односторонних пределов функции
справа и слева.
|
|||||||
7.9 |
Условие |
Варианты |
|||||
Дана
функция
|
|
||||||
Решение
|
|||||||
7.10 |
Условие |
Варианты |
|||||
Дана
функция
|
|
||||||
Решение
|
|||||||






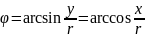

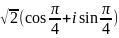 в алгебраической форме:
в алгебраической форме:
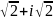
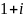
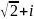
 .
.

 .
. равна:
равна: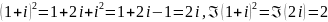 .
.
 равен
равен
 .
.

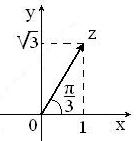
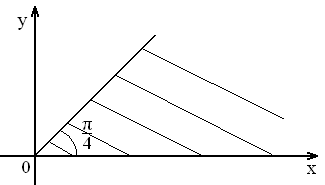
 На
рисунке представлена геометрическая
иллюстрация комплексного числа
,
тогда тригонометрическая форма записи
этого числа имеет вид:
На
рисунке представлена геометрическая
иллюстрация комплексного числа
,
тогда тригонометрическая форма записи
этого числа имеет вид:




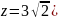 .
.




 ,
, тригонометрическая
форма
тригонометрическая
форма показательная
форма
показательная
форма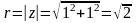


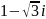 в тригонометрической форме имеет вид:
в тригонометрической форме имеет вид: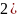
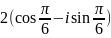




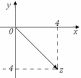 а
рисунке приведено геометрическое
изображение комплексного числа. Его
тригонометрическая форма записи имеет
вид …
а
рисунке приведено геометрическое
изображение комплексного числа. Его
тригонометрическая форма записи имеет
вид …
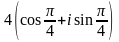

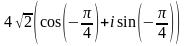




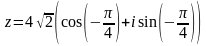 .
.


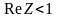
 (в) 2)
(в) 2)
 (д)
(д) (г) 4)
(г) 4)
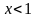 (а)
(а) ,
то модуль числа z
равен …
,
то модуль числа z
равен … т.к.
т.к.
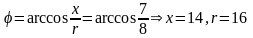 .
.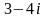 2)
2)
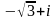
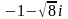 4)
4)
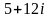

 (а)
(а) (д)
(д) (в)
(в) (б)
(б) равен:
равен: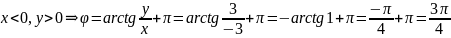 .
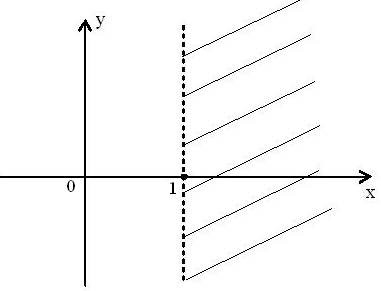
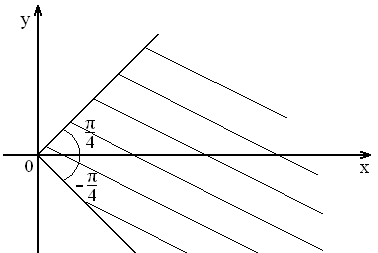
. а
рисунке представлена геометрическая
иллюстрация комплексного числа
,
тогда тригонометрическая форма записи
этого числа имеет вид:
а
рисунке представлена геометрическая
иллюстрация комплексного числа
,
тогда тригонометрическая форма записи
этого числа имеет вид:
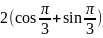

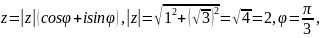
 .
. имеет вид:
имеет вид:

 ;
;
 ;
;
 ;
;
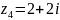 .
. ;
; ;
;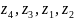 ;
;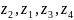 .
. ;
; ;
; ;
; .
.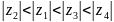 .
Верный ответ г).
.
Верный ответ г).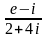 .
.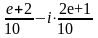
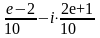

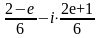
 и
и
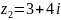 .
.
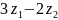 равно:
равно:



 .
.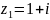 и
и
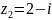 ,
тогда
,
тогда
 равно:
равно:
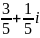


 .
. ,
то
,
то
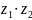 равно:
равно:
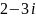
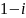
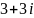
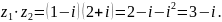
 . Установить соответствия между
операциями над данным числом и
результатами их выполнения:
. Установить соответствия между
операциями над данным числом и
результатами их выполнения:

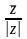




 (д)
(д)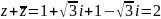 (б)
(б) (а)
(а) (в)
(в) .
Известно, что
.
Известно, что

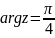 ,
тогда
,
тогда
 равно …
равно …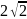
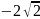

 ,
комплексное число z
можно возвести в n-ую
степень по формуле Муавра
,
комплексное число z
можно возвести в n-ую
степень по формуле Муавра
 .
.

 на комплексное число
на комплексное число
 является:
является: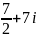
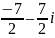
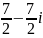
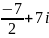
 .
.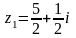 и
и
 равна …
равна …

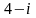

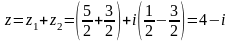 .
.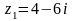 и
и
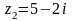 .
Тогда действительная часть произведения
.
Тогда действительная часть произведения
 равна …
равна … .
.
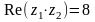 .
. и
и



 (в градусах) равен …
(в градусах) равен …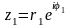 ,
,
 ,
,
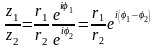 ,
, .
. от деления двух комплексных чисел,
где
от деления двух комплексных чисел,
где
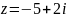 равно:
равно:


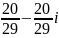
 .
.

 на сопряженное
на сопряженное
 равно:
равно: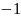


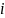

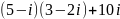
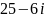

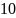

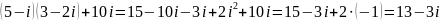 .
. является число равное:
является число равное: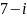







 . Установить соответствия между
операциями над данным числом и
результатами их выполнения:
. Установить соответствия между
операциями над данным числом и
результатами их выполнения:



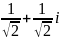
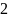
 (д)
(д)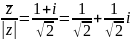 (г)
(г) (а)
(а) (б)
(б)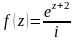 .
Тогда
.
Тогда
 равно …
равно …


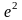
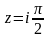 .
Имеем
.
Имеем .
. в т.
в т.
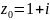 равно:
равно: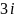


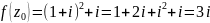 .
.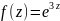 ,
где
,
имеет вид:
,
где
,
имеет вид: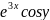
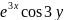


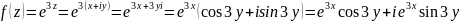 .
.
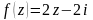 в точке
в точке
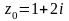 равно …
равно …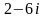

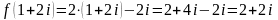
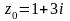
 ;
2)
;
2)
 ;
3)
;
3)

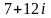
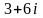

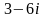
 (г)
(г) (д)
(д)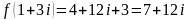 (б)
(б)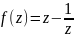 в точке
в точке
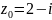 равно:
равно:
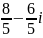


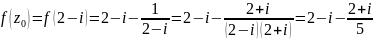
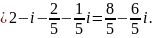
 в точке
в точке
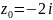 равно:
равно:



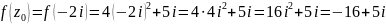
 ,
тогда значение производной этой
функции в т.
,
тогда значение производной этой
функции в т.
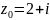 равно:
равно:
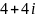

 .
. ,
то
,
то
 имеет вид:
имеет вид:


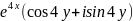
 т.к.
т.к.
 то
то .
.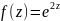 в точке
в точке
 равно:
равно:
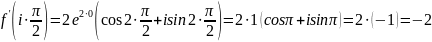
 ,
тогда значение производной этой
функции в точке
,
тогда значение производной этой
функции в точке
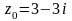 равно …
равно …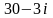


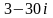

 ,
тогда значение производной этой
функции в точке
равно:
,
тогда значение производной этой
функции в точке
равно: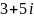
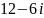


 .
. ,
2)
,
2)
 ,
4)
,
4)
 .
. ,
при которых период функции
,
при которых период функции
 равен
равен
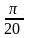 ,
равен …
,
равен …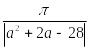 ,
поэтому
,
поэтому
 2)
2)
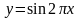
 4)
4)
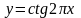
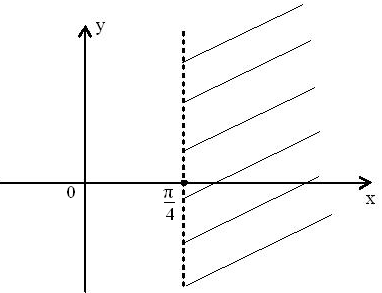
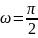 ,
отсюда
,
отсюда
 .
Для
.
Для
 ,
отсюда
,
отсюда
 .
Для
.
Для
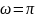 ,
отсюда
,
отсюда
 .
Для
,
отсюда
.
Для
,
отсюда
 .
Следовательно, период 2 имеют функции
1 и 3.
.
Следовательно, период 2 имеют функции
1 и 3.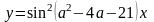 равен
равен
 ,
равно …
,
равно … имеет период
,
тогда рассматриваемая функция имеет
период
имеет период
,
тогда рассматриваемая функция имеет
период
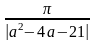 ,
поэтому
,
поэтому
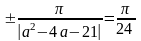 .
Откуда получаем два уравнения:
.
Откуда получаем два уравнения:


 2)
2)



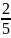
 (б). Для
,
отсюда
(а). Для
(б). Для
,
отсюда
(а). Для
 ,
отсюда
,
отсюда
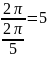 (г).
(г).
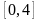 имеет вид …
имеет вид …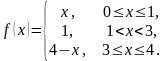
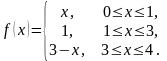
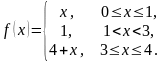

 функция
функция
 ,
при
,
при
 функция
функция
 ,
а при
,
а при
 функция
функция
 .
Поэтому аналитическое представление
функции
имеет вид:
.
Поэтому аналитическое представление
функции
имеет вид:
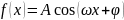
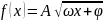

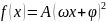
 описывает гармоническое колебательное
движение, то частотой колебания
называется величина …
описывает гармоническое колебательное
движение, то частотой колебания
называется величина …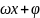
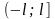 имеет вид …
имеет вид …
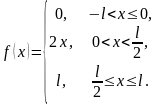

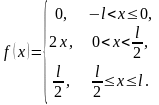
 функция
функция
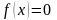 ,
при
,
при
 функция
,
а при
функция
,
а при
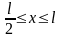 функция
функция
 .
Поэтому аналитическое представление
функции
имеет вид:
.
Поэтому аналитическое представление
функции
имеет вид:
 ряда Фурье функции
ряда Фурье функции
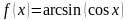 с периодом
равен …
с периодом
равен …

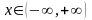 .
Принимая во внимание четность данной
функции, имеем
.
Принимая во внимание четность данной
функции, имеем
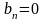 ,
то есть
,
то есть
 .
. и его периодическое продолжение заданы
на рисунке:
и его периодическое продолжение заданы
на рисунке: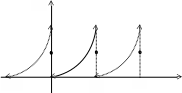


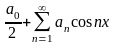
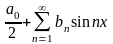
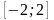 ,
является четной. Тогда разложение
этой функции в ряд Фурье может иметь
вид …
,
является четной. Тогда разложение
этой функции в ряд Фурье может иметь
вид …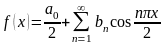

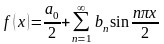
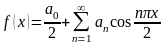
 .
Тогда ее разложение имеет вид г.
.
Тогда ее разложение имеет вид г.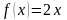 ,
,
 .
Тогда коэффициент
.
Тогда коэффициент
 разложения функции
в ряд Фурье равен …
разложения функции
в ряд Фурье равен …
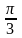

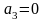



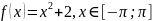 . Тогда коэффициент
. Тогда коэффициент
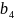 разложения функции
в ряд Фурье равен:
разложения функции
в ряд Фурье равен:


 – четная
функция, т.к.
– четная
функция, т.к.
 ,
следовательно,
,
следовательно,
 .
. ряда Фурье периодической функции
с периодом 2, заданной на отрезке
ряда Фурье периодической функции
с периодом 2, заданной на отрезке
 уравнением
уравнением
 ,
равен …
,
равен … ;
;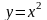 является четной, поэтому при вычислении
a0
используем
формулу
является четной, поэтому при вычислении
a0
используем
формулу
 соотношением
соотношением ,
равен …
,
равен … ;
;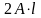 ;
;
точка разрыва I-го
рода. Согласно теореме о разложении
функции в ряд Фурье, функция может
быть представлена указанным рядом.
Имеем
точка разрыва I-го
рода. Согласно теореме о разложении
функции в ряд Фурье, функция может
быть представлена указанным рядом.
Имеем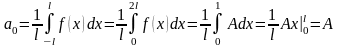 .
. .
.
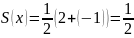 .
. . Тогда коэффициент
. Тогда коэффициент
 разложения функции
в ряд Фурье равен:
разложения функции
в ряд Фурье равен: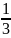
 – нечетная
функция, т.к.
– нечетная
функция, т.к.
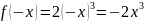 ,
следовательно,
,
следовательно,
 .
. . Тогда коэффициент
. Тогда коэффициент
 разложения функции
в ряд Фурье равен:
разложения функции
в ряд Фурье равен:

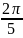
 – четная
функция, т.к.
– четная
функция, т.к.
 ,
следовательно
,
следовательно
 .
.