2. Матрицы

Матрицей А размерности m n называется прямоугольная таблица из m строк и n столбцов, состоящая из элементов (i = j = ).

Если m=n , то матрица называется квадратной , m n – прямоугольной.

Единичной матрицей Е называется квадратная диагональная матрица с единицами на главной диагонали (det E=1); нулевой называется матрица, все элементы которой равны нулю.

Две матрицы A и B называются равными ( A = B ) , если они имеют одинаковое число строк и столбцов и их соответствующие элементы совпадают

Суммой матриц A = и B = ( i = ; j= ) называется матрица C = , где , ( i = ; j = ), т.е. С=A+B.

Произведением матрицы А = (i = ; j = ) на вещественное число называется матрица С = (i= ; j = ) , т.е. С = А.

Произведением С = АВ матрицы А = , ( i = j = ) на матрицу В = ( i = ; j = ) называется матрица С = , ( i =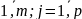 ), имеющая порядок m p , элементы определяются формулой

i = 1,2, m ; j = 1,2, p.

Матрицу А можно умножить на матрицу В, если число столбцов матрицы А равно числу строк матрицы В и получается матрица, у которой, столько строк сколько их имеет матрица - множимое и столько столбцов, сколько их имеет матрица - множитель.

Если АВ=ВА, то матрицы называются перестановочными (коммутативными).

А²=А А

Матрица, у которой строки поменяны местами со столбцами, называется транспонированной по отношению к первой матрице.

Матрица называется невырожденной, если det A =

Обратной матрицей для квадратной невырожденной матрицы А, называется матрица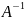 , удовлетворяющая условию

где - алгебраические дополнения

Собственные числа и собственные векторы матрицы

Характеристическим уравнением матрицы А =

называется уравнение

Корни этого уравнения называются характеристическими числами матрицы.

Система уравнений

в которой имеет одно из значений , определяет тройку чисел , соответствующую данному характеристическому числу. Эта совокупность трёх чисел определяет вектор

называемый собственным вектором матрицы.

Матричные уравнения и их решения

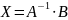
, то

, то

, то

где А, В, С, - заданные матрицы; Х-искомая матрица .

Рангом матрицы называется наибольший из порядков её миноров отличных от нуля.

Системы линейных алгебраических уравнений

Рассмотрим систему m линейных уравнений с n неизвестными

Система называется совместной , если она имеет решение и несовместной, если она не имеет решений.

Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой, если она имеет бесчисленное множество решений.

Две совместные системы уравнений называются равносильными, если каждое решение первой системы является решением второй и обратно.

Теорема Кронекера-Капелли

Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы

был равен рангу её расширенной матрицы

полученной путём добавления к матрице А столбца из свободных членов системы.

Следствие 1. Если r(A) = r(B) = n – числу неизвестных, то система имеет единственное решение.

Следствие 2. Если r(A) = r(B) < n , то система имеет бесчисленное множество решений, зависящих от (n–r) параметров (свободных неизвестных).

Формулы Крамера

Для системы, состоящей из трёх уравнений с тремя неизвестными, формулы Крамера имеют вид:

где , , =

Из формул Крамера следует:

1. система имеет единственное решение;

2. , но хотя бы один из , то система не имеет решения;

3. , то система имеет бесчисленное множество решений или совсем не имеет решения.

Система m уравнений с n неизвестными вида:

называется линейной однородной системой.

Следуя формулам Крамера, можно сделать выводы:

1. , m=n система имеет единственное нулевое решение.

2. , m n система имеет бесчисленное множество решений и среди этих решений могут быть и ненулевые.

Однородная система уравнений всегда совместна и имеет ненулевое решение только тогда, когда определитель системы равен нулю .