4. В стовпчик е копіюємо дані стовпчика в (Межі інтервалів 1).
5. В клітинку F2 (Висоти) записуємо формулу: =C2/(B3-B2). Копіюємо цю формулу в діапазон F3:F8.
Для побудови гістограми послідовно виконуємо:
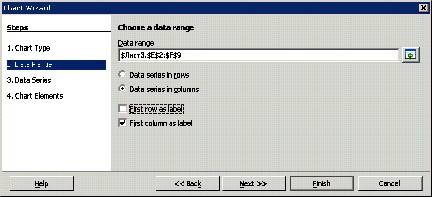
Результати виконання команд:
Побудова полігону частот і відносних частот.
Для побудови полігонів необхідно в стовпчики А, В скопіювати стовпчики E, F, G лабораторної роботи № 3.
6. Побудова полігону частот.
Для побудови полігону частот послідовно виконуємо:
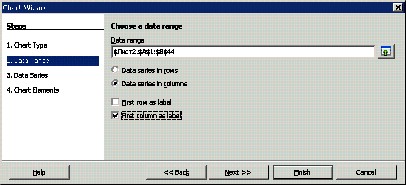
Результати виконання команд:
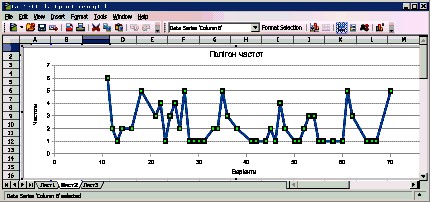
7. Побудова полігону відносних частот.
Для побудови полігону відносних частот послідовно виконуємо:
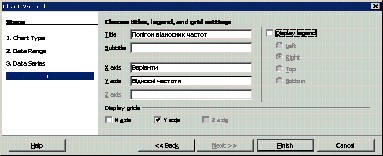
Результати виконання команд:
Оформити звіт.
Індивідуальне завдання: виконати відповідне варіанту завдання (побудувати полігон частот, відносних частот і гістограму розподілу для середньої тривалості життя).
Лабораторна робота № 18
Тема
Інтервальне оцінювання параметрів нормального розподілу .
Мета
Уміти будувати надійні інтервали для основних числових характеристик вибірки, нормального розподілу.
Теоретичні відомості
Опрацювати матеріал Лекції № 4 “ Статистична оцінка параметрів розподілу генеральної сукупності”.
В лабораторній роботі використовуються функції:
СРЗНАЧ (AVERAGE) — повертає середнє арифметичне аргументів.
Синтаксис: AVERAGE(число1;число2;...)
Число1, число2, ... – це від 1 до 30 аргументів, для яких обчислюється середнє.
Зауваження
Аргументи мають бути або числами, або іменами, масивами або посиланнями, що містять числа.
Якщо аргумент, що є масивом або посиланнями, містить тексти, логічні значення або порожні клітинки, то такі значення ігноруються; але клітинки, які містять нульові значення, враховуються.
ДИСП(VAR) – обчислює дисперсію на основі вибірки.
Синтаксис: VAR(число1;число2;...)
Число1, число2, ... – це від 1 до 30 числових аргументів, які відповідають вибірці з генеральної сукупності.
СТАНДОТКЛОН (STDEV) - обчислює стандартне відхилення на основі вибірки.
Синтаксис: STDEV(число1;число2; ...)
Число1, число2, ... – це від 1 до 30 числових аргументів, які відповідають вибірці з генеральної сукупності.
СЧЁТ (COUNT) − підраховує кількість клітинок усередині діапазону.
Синтаксис: COUNT(діапазон)
діапазон – це діапазон, в якому потрібно підрахувати кількість клітинок.
ДОВЕРТИ(CONFIDENCE) - Возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности.
Синтаксис: ДОВЕРИТ(альфа ;станд_откл;размер)
Альфа — це рівень значущості. Рівень надійності = (1 - альфа)*100%,.
Станд_откл — це стандартне відхилення генеральної сукупності для діапазону даних.
Размер — це розмір вибірки.
ХИ2ОБР(CHIINV) – Повертає значення, обернене до односторонньої ймовірності розподілу (хі-квадрат).
Якщо ймовірність = ХИ2РАСП(x;...), то ХИ2ОБР(ймовірність;...) = x.
Функція використовується для порівняння спостережуваних результатів зі сподіваними, для того, щоб зробити висновок чи нульова гіпотеза є обґрунтованою.
Синтаксис: ХИ2ОБР(вероятность;степени_свободы)
Вероятность — це ймовірність, пов’язана з розподілом (хі-квадрат).
Степени_свободы — це число ступенів свободи.