8.2. Метод вариации произвольных постоянных (метод Лагранжа)

1. Для уравнения (11) составляют соответствующее однородное уравнение (12) и находят его общее решение y_о.о.:

. (14)

2. В уравнении (14) полагают константы функциями от x, т.е. . Эти функции находят из системы:

Решают эту систему методом Крамера. Определитель этой системы – определитель Вронского (он будет отличен от нуля для линейно независимых функций).

.

,...,

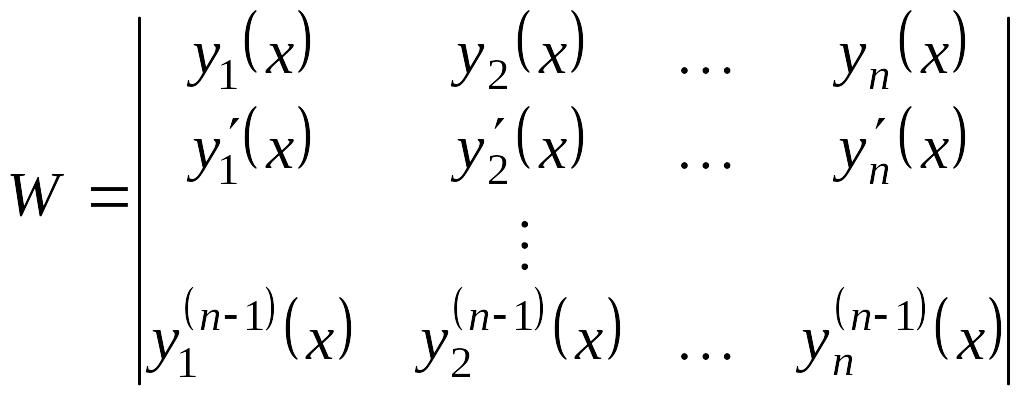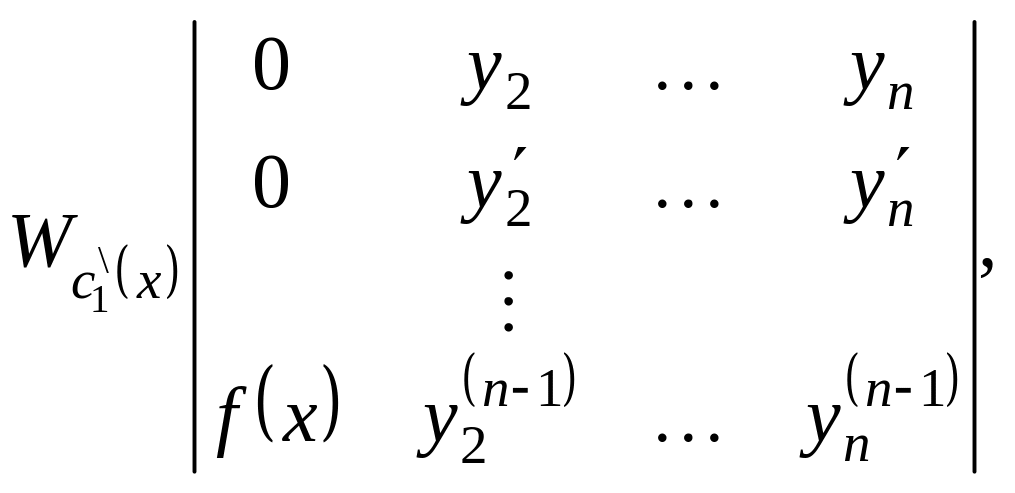
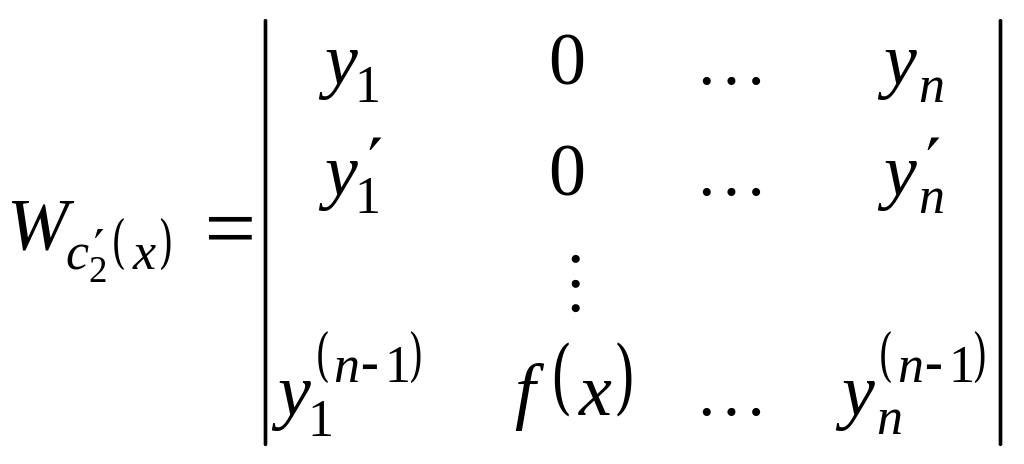Тогда: . Отсюда .

Подставляя эти значения в (14), получим общее решение уравнения (11):

Задача 16. Найти решение задачи Коши .

Решение. Воспользуемся методом вариации произвольных постоянных. (Следует иметь в виду, что метод имеет место, когда коэффициент при старшей производной равен единице!)

Найдем общее решение уравнения ; т.к. корнями характеристического уравнения являются числа , то .

Предполагая, что с₁ и с₂ – есть функции от x, будем искать решение исходного уравнения в виде , где c₁(x) и c₂(x) найдем из системы:

Составим определитель этой системы – определитель Вронского:

.

(Т.к. определитель отличен от нуля, система имеет решение и при том единственное.)

.

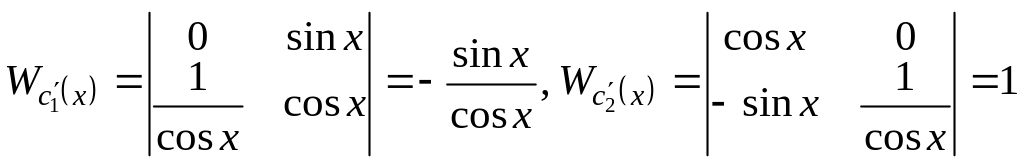Тогда . Отсюда, интегрированием находим

.

Таким образом, общее решение исходного уравнения будет выглядеть так:

.

Для решения задачи Коши найдем :

.

Подставляя начальные условия в и найдем, что с₁=1, с₂=0. Тогда — частное решение.

9. Задачи механики и физики, приводящие к составлению и решению дифференциальных уравнений

Решим несколько задач из физики и механики, которые требуют составления дифференциального уравнения первого порядка и его интегрирования.

В задачах приведенных в этом разделе, несмотря на их внешнее различие две переменные величины х и время t, участвующие в них, обладают тем общим свойством, что скорость изменения одной них (х) по отношению к другой (t) пропорциональна наличному количеству величины х в рассматриваемый момент времени.

Учитывая, что скорость изменения величины х есть производная , обозначим через k коэффициент пропорциональности. Тогда дифференциальное уравнение, описывающее этот процесс, будет иметь вид

(15)|

Это уравнение с разделяющимися переменными и интегрируется оно очень просто.

Разделяя переменные, получим

; ,

или

, ,

(16)

Таким образом, решением уравнения (15) является показательная функция.

Условие задачи должно содержать данные:

1) для определения произвольной постоянной, т. е. значение х₀ величины х в момент времени : ;

2) для определения коэффициента пропорциональности k.

Уравнение (15) описывает процесс непрерывного роста или непрерывного убывания величины х, причем, как видно из решения (16), рост имеет место при положительном коэффициенте пропорциональности k, а убывание — при отрицательном k.

Задача 1. Скорость распада радия пропорциональна количеству нераспавшегося радия. Количество радия в начале процесса (t = 0) было равно х₀. Известно, что за 1600 лет распадается половина первоначального количества.

1) Через сколько лет количество нераспавшегося радия будет составлять 80% первоначального?

2) Определить, какой процент радия сохранится через 300 лет.

Решение. Уравнение (15) описывает процесс радиораспада. Определим в (17,27) произвольную постоянную С. Известно из условия задачи, что в начальный момент, т.е. при t = 0, количество радия равно х₀. Таким образом, начальное условие: . Подставляя в (16) t = 0; х = х_о, получим

;

а потому (16) перепишется так:

. (17)

Задача содержит условие, позволяющее определить коэффициент пропорциональности k: когда t = 1600, количество радия х равно половине начального, т.е. . Подставляя в (17) вместо х и 1600 — вместо t, получаем . Сокращая на х₀, получим . Для определения k, прологарифмируем по основанию е обе части этого равенства:

; ; .

Теперь решение (17) перепишется в виде

(18)

Ответим на первый вопрос задачи. По условию (80%). Подставляя это значение в последнее уравнение, имеем

Для определения t прологарифмируем обе части равенства!

,

Отсюда

лет.

Чтобы ответить на второй вопрос задачи, найдем из (17,29) отношение при t = 300:

; .

Таким образом, через 300 лет сохранится 87,8% начального количества радия, а следовательно, распадется за 300 лет 12,2%.

Задача 2 (для самостоятельного решения).

Согласно закону Ньютона, скорость охлаждения нагретого тела пропорциональна разности температур тела и окружающей среды.

Определить, за какое время тело, нагретое до температуры х₀ = 300°, помещенное в жидкость, температура которой 60° охладится до 150°, если считать количество жидкости настолько большим, что ее температура практически остается без изменения. При этом известно, что через 10 минут после начала процесса температура тела равна 200°.

Указание. Обозначить через х непрерывно убывающую температуру тела ( ). Разность температур тела и жидкости равна х-60°. Скорость охлаждения — . Если k — коэффициент пропорциональности, то дифференциальное уравнение процесса будет таким:

.

Общее решение имеет вид

(19)

Начальное условие: в начальный момент времени t = 0 температура х₀ = 300°:

; .

Поэтому (17,30) запишется так:

(20)

Для определения коэффициента пропорциональности k исполь­зуем дополнительное условие в задаче:

при t = 10 мин температура тела равна 200°. Поэтому из (17,31) при , t = 10, 200 = 60 + 240 . Откуда следует, что k = - 0,053, и тогда уравнение (20), связывающее температуру х и время t, запишется так:

х = 60 + 240 .

Чтобы ответить на вопрос задачи, надо подставить сюда х = 150 и определить t.

Окажется, что

Ответ. t = 18,5 мин.

Задача 3. Точка движется по прямой с постоянным ускорением, равным . В начальный момент t = 0, ее скорость , а расстояние от начала координат —S₀, т.е. , .

Найти закон движения.

Решение. При движении по прямой ускорение есть производная от скорости по времени, а потому ускорение ; . Интегрируя, получим . Подставляя сюда t = 0, , найдем , а потому уравнение, связывающее скорость и время, перепишется так:

.

Известно, что скорость в прямолинейном движении — производная от пути по времени: .

Поэтому , , а .

Используя начальное условие S = So при t = 0, получим, что С₂= So, и закон движения запишется следующим образом:

.

Если , то — хорошо известный из физики закон прямолинейного равномерно-переменного движения.

Задача 4. Определить форму зеркала, отражающего все лучи, исходящие из одной точки так, чтобы после отражения они были параллельны заданному направлению.

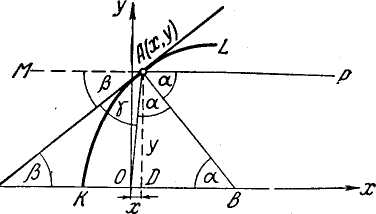
Решение. Поместим начало координат точку, из которой исходят лучи, а заданное направление, которому должны быть параллельны отраженные лучи, примем за ось Ох (см. рис. 4).

Рис. 4

Пусть точка А принадлежит зеркалу, а АP — один из таких лучей. Кривая АК — линия пересечения зеркала с плоскостью хОу. Согласно известному закону оптики, лучи падающий, отраженный и нормаль к поверхности, на которую падает луч, лежат в одной плоскости и составляют с нормалью равные углы (угол падения равен углу отражения). На рис. 4 АВ — нормаль к кривой KL в точке А (х, у), ОА — падающий луч, АР — отраженный. Поэтому < ОАВ= < ВАР = . Треугольник ОАВ — равнобедренный: ОА = ОВ. Сумма углов с общей вершиной в точке А, расположенных по одну сторону от MP, равна 180°. Поэтому, так как  +  = 90°, то и + β= 90°. Значит,  +  = + β, а  = β. Отсюда заключаем, что треугольник СОА — равнобедренный: ОС = ОА.

Если уравнение искомой кривой y = f(x), то . Но с другой стороны . Так как , , то . Подставляя сюда , получаем дифференциальное уравнение

,

которое не изменяется от замены x на kx, а y на ky, а потому оно является однородным. Применяя подстановку , получим уравнение с разделяющими переменными

,

а после разделения переменных

Иметь в виду, что удобно вычислить при помощи подстановки . Окажется, что он равен — .

Ответ. — семейство парабол.

Зеркало должно иметь форму параболоида вращения. Докажите, что начало координат есть фокус параболы.

Задача 5. В сопротивлении материалов доказывается, что дифференциальное уравнение упругой линии консоли с постоянным поперечным сечением и сосредоточенной на свободном конце силой Р имеет вид

где w — прогиб консоли в сечении с абсциссой х, a EI — постоянная величина, так называемая жесткость на изгиб сечения балки.

Найти решение этого уравнения, удовлетворяющее начальным условиям:

; .

Решение. Применив формулу

(**)

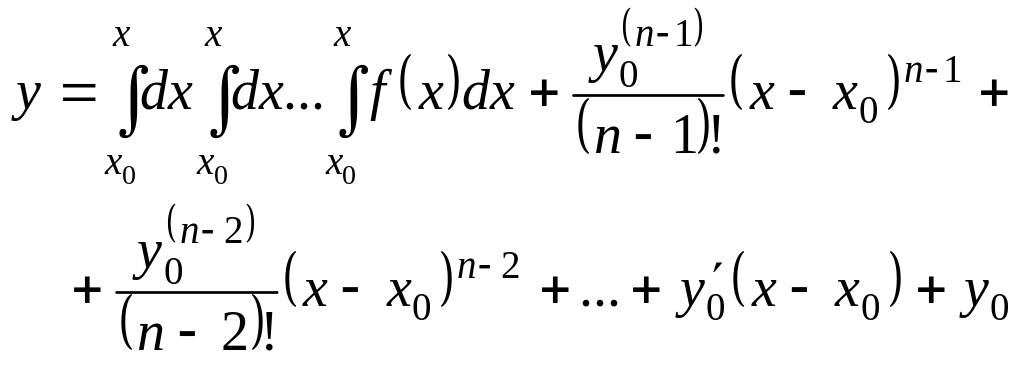при п = 2 и х₀ = l, получим

(два последних слагаемых в этой формуле исчезают, так как имеют место нулевые начальные условия);

. (21)

Если не пользоваться сразу готовой формулой (**) (хотя в этом нет ничего предосудительного), то интегрирование уравнения можно провести так.

Первое интегрирование даст

.

Учитывая второе начальное условие , получаем уравнение для определения произвольной постоянной

; .

Поэтому

.

Интегрируя вторично, получаем

.

Используя первое начальное условие, находим

откуда

,

и поэтому окончательно

,

что, как легко видеть, совпадает с полученным ранее решением. Полученное уравнение (21) — уравнение упругой линии консоли. Из него видно, что эта линия — кубическая парабола (парабола третьей степени).

Задача 6 (для самостоятельного решения).

Дифференциальное уравнение изогнутой оси простой балки постоянного сечения, несущей сплошную равномерно распределенную нагрузку интенсивностью q, имеет вид

(EI имеет прежнее значение, l — длина балки).

Краевые условия (иногда они называются граничными):

при х = 0 w = 0, иначе: w (0) = 0;

при х = l до = 0, иначе: w (l) = 0,

т. е. на концах балки прогиб равен нулю.

Ответ. Общее решение

.

Задача 7 (прямолинейное движение материальной частицы).

При движении точки по прямой, принимаемой за ось Ох, основное уравнение движения точки записывается так:

, (22)

где т — масса точки; — ускорение, a F_x — проекция действующей на точку силы на ось Ох.

Найти закон движения точки, падающей под действием силы тяжести, учитывая, что в начальный момент t = t₀ ее координата х — х₀, а начальная скорость равна v₀.

Решение. Направим ось Ох вертикально вниз и обозначим через g ускорение силы тяжести.

Уравнение движения (22) запишется так;

Сокращаем на m и получаем

.

Умножаем на dt обе части равенства:

Но , поэтому . Интегрируя, имеем . При t = t₀ начальная скорость v = v₀. Подставляя эти значения, получаем

; .

Теперь

;

Интегрируя вторично, находим

.

Ho x = x₀ при t = t₀, а потому ; . Подставив это значение С₂, получим окончательно

.

Если t₀ = 0, то

.

З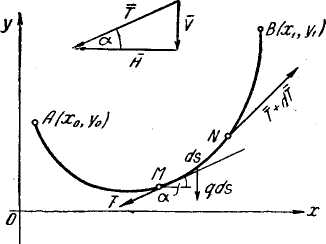 адача 8 (задача о цепной линии).

Найти уравнение кривой, по которой расположится гибкая нерастяжимая нить, укрепленная концами в двух данных точках А (х₀, у₀) и В (х_ъу_г), под действием нагрузки, равномерно распределенной по ее длине, причем нагрузка, приходящаяся на единицу длины, равна .

Рис. 5

Решение. Вырежем на кривой элемент дуги MN = ds. На него действуют такие силы: в точке М — натяжение , в точке N — натяжение и сила тяжести, численно равная ds.

Условия равновесия требуют, чтобы суммы проекций этих сил на оси координат были равны нулю.

Сумма проекций всех сил на ось Ох:

(проекция силы ds на ось Ox равна нулю)

. (23)

Сумма проекций всех сил на ось Оу:

;

,

откуда

(24)

Обозначим для удобства горизонтальную проекцию натяжения через H, а вертикальную проекцию — через V. Тогда уравнения равновесия (23) и (24) запишутся так:

; . (25)

Из следует, что H =const, т.е. горизонтальная проекция натяжения нити — величина постоянная. Обозначим через  угол, который касательная к нити в точке M составляет с осью Ox.

Второе уравнение в (25) преобразуем так:

; ; .

(Величина H, как постоянная, вынесена за знак дифференциала). Дифференциал дуги . Подставляя эти значения dV и ds во второе уравнение (25), получим

,

и окончательно дифференциальное уравнение искомой линии будет таким:

. (26)

Обозначим = а и введем подстановку . Тогда , и уравнение (26) станет таким:

.

Это уравнение с разделяющимися переменными. После разделения переменных получим

.

Интегрируя уравнение, найдем

,

откуда

(27)

Из (27) надо определить р. Это проще всего сделать так: умножим обе части (27) на и получим

,

или

Отсюда, умножая обе части равенства на , получаем

. (28)

Складываем почленно (27) и (28):

,

а

.

Правая часть последнего равенства есть , а . Поэтому последнее равенство перепишется так:

или .

Интегрируя, находим

(29)

Перепишем (29) в виде

(30)

и перенесем начало координат в точку , а новые координаты точки на кривой обозначим по-прежнему через х и у. Уравнение (29) перепишется в виде

.

Это уравнение цепной линии. Итак, искомая кривая — цепная линия.

Задача 9. Найти закон прямолинейного движения материальной точки массы т, которая падает в среде, сопротивление которой пропорционально второй степени скорости. Начальные условия: в начальный момент движения t=0 координата точки равна х₀, а начальная скорость v = v₀. (см. рис. 6).

Решение. На точку действуют две силы: вес и сила сопротивления . Примем прямую, по которой про исходит движение, за ось Ох, и направим ее вертикально вниз.

Основным уравнением динамики точки является уравнение

(30)

где — равнодействующая всех сил, действующих на точку.

Так как сила сопротивления по условию пропорциональна квадрату скорости, то ее модуль , где k²m — коэффициент пропорциональности. Спроектируем на ось Ох действующие на точку силы:

.

Знак минус перед k²mv² объясняется тем, что сила сопротивления всегда направлена в сторону, противоположную движению.

П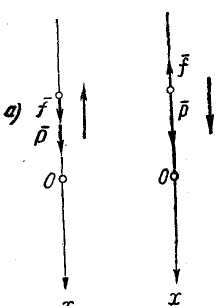 роекция ускорения на ось Ох равна , а проекция скорости на ту же ось есть , а потому (30) перепишется в виде

.

Сокращая на т, получим уравнение

Рис. 6

,

которое является дифференциальным уравнением движения точки. Это уравнение не содержит искомой функции х. Сделаем подстановку: . Порядок уравнения понизится на единицу и оно перепишется так:

.

Переменные в этом уравнении разделяются, получается следующее уравнение:

.

Интегрируя, имеем

,

или

. (31)

Так как при t = 0 скорость равна v_0, то для определения С₁ получаем уравнение

и уравнение (31) запишется в виде

Определим отсюда р:

;

.

Решая это уравнение относительно , получим

. (32)

Умножим числитель и знаменатель дроби на . Тогда

.

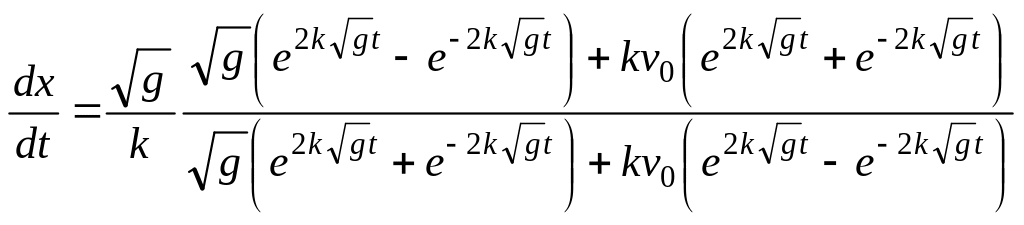Вводя гиперболические синус и косинус и сокращая на 2, получим

. (33)

Если в правой части уравнения числитель умножить на , то он станет производной знаменателя. Замечая это, разделяем переменные и интегрируя получаем

.

Определим произвольную постоянную С₂.

На основании начальных условий х = х₀ при t = 0. Поэтому

;

.

Окончательно

Уравнение (33) дает закон изменения скорости в зависимости от времени. Очевидно, что при неограниченном возрастании времени (t→∞) дробь в правой части этого уравнения стремится к единице, а скорость . Отсюда мы можем заключить, что движение точки асимптотически приближается к равномерному, скорость которого равна , причем эта скорость не зависит от начальных условий.

Задача 10. Найти решение линейного однородного дифференциального уравнения, удовлетворяющего указанным начальным условиям:

; ; .

Решение. Это уравнение является уравнением свободных гармони­ческих колебаний. Оно имеет очень важное значение в механике и других прикладных науках.

Характеристическое уравнение имеет вид ; ; — корни комплексные сопряженные, причем  = 0; .

Частные решения, имеют вид:

; .

Следует запомнить, что когда действительная часть комплексного корня характеристического уравнения равна нулю, т.е. когда корни чисто мнимые, то частные решения содержат только тригонометрические функции, множитель же е^х при них отсутствует, так как при  = 0 е^х = 1.

Общее решение:

; (34)

(рекомендуется запомнить это общее решение уравнения свободных гармонических колебаний. Встречаться оно будет очень часто).

Определяем С₁ и С₂ из начальных условий:

.

Отсюда . Подставляя эти значения произвольных постоянных в (34), получаем искомое решение в виде

.

Это решение выгодно представить в другом виде. Положим

; . (35)

Тогда

.

Окончательно

(36)

Возводя в квадрат обе части каждого из равенств (35) и складывая их почленно, получим:

; .

Механический смысл величин А,  и φ: А — амплитуда колебаний;  — частота колебаний; φ —начальная фаза.

Движение, определяемое рассматриваемым уравнением ,— периодическое. Его период .

Задача 11 (для самостоятельного решения).

Материальная точка массы т движется по прямой, притягиваемая к неподвижному центру силой, прямо пропорциональной расстоянию точки от центра притяжения. Сопротивление среды отсутствует. Определить закон движения точки, если в начальный момент движения t =0, х = х₀, v = - v₀, т. е. х(0)= =х₀, v (0) = v₀.

Решение. Прямую, по которой происходит движение точки, примем за ось Ох, причем положительным будем считать направление направо. Начало координат поместим в центр притяжения. Коэффициент пропорциональности возьмем для удобства последующих выкладок равным k²m. Сила притяжения

здесь — расстояние точки от начала координат.

Определим модуль силы .

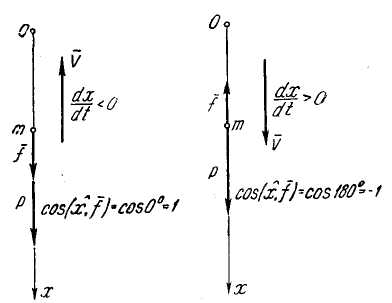
М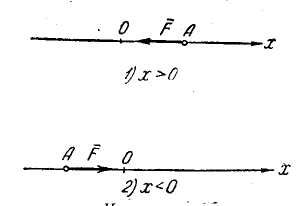 одуль вектора — величина положительная. Поэтому перед модулем силы надо поставить знак плюс, когда точка находится справа от начала координат (x>0), и знак минус, когда она находится слева от него (х<0). Таким образом, модуль силы

(А)

Рис. 7

Когда точка находится справа от начала координат (х > 0), то сила притяжения к началу координат направлена в отрица­тельную сторону оси Ох, а потому составляет с осью Ох угол в 180°, a .

Если же точка находится слева от начала координат (х < 0), сила притяжения направлена в положительную сторону оси Ох и составляет с нею угол в 0°, а потому .

Таким образом, , причем верхний знак соответствует х > 0, а нижний х < 0.

Известно, что проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью. Умножая (А) на , получаем

, (В)

независимо от того, где находится на оси Ох притягиваемая точка.

Подставляя это значение проекции силы в основное уравнение динамики:

,

получаем дифференциальное уравнение движения

(37)

и, сокращая на т, имеем

Перепишем это уравнение в виде

(С)

Это уравнение, как мы уже говорили, называется уравнением свободных гармонических колебаний. Мы замечаем, что оно является линейным однородным уравнением второго порядка (искомая функция — х, независимая переменная —t). Его характеристическим уравнением будет

(D)

Неизвестное характеристического уравнения мы обозначили не буквой k, как это было в предыдущих задачах, а l, так как k входит уже в коэффициент пропорциональности.

Решая уравнение (D), находим, что l = ±ki, а потому частными решениями уравнения (D) будут:

; ,

и его общее решение

.

Из начальных условий задачи следует, что , (определите это самостоятельно), поэтому решением задачи, удовлетворяющим начальным условиям, будет

(E)

Далее удобно поступить так, как это было сделано в задаче 10, и тогда решение (Е) запишется так:

,

где

; .

Задача 12 (для самостоятельного решения).

Материальная точка массы т движется по прямой, отталкиваемая от неподвижного центра силой, пропорциональной расстоянию. Начальные условия: ; .

Указание. Дифференциальным уравнением движения будет

Общее решение:

.

Из начальных условий определяем C₁ и С₂:

; ;

,

или, используя формулы

получим

.

З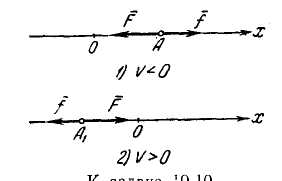 адача 13. Материальная точка массы т движется по прямой, притягиваемая к неподвижному центру силой , прямо пропорциональной расстоянию точки от центра притяжения. Сила сопротивления среды прямо пропорциональна первой степени скорости.

Начальные условия: в начальный момент движения (t = 0) ; .

Рис. 8

Решение. Эта задача отличается от задачи 11 тем, что здесь учитывается сила сопротивления среды. Обозначим для удобства последующих выкладок коэффициент пропорциональности через 2hm (h > 0). Если точка движется в положительном направлении оси Ох, то ее абсцисса с течением времени возрастает, а скорость > 0. Если же точка движется в отрицательном направлении оси, то ее абсцисса убывает с течением времени, а следовательно, ее скорость < 0. Так как сила сопротивления всегда направлена в сторону, противоположную скорости, то . Таким образом, на точку действует сила притяжения ; (см. задачу 11) и сила сопротивления . Сумма проекций этих сил на ось Ох равна , и дифференциальное уравнение движения, согласно второму закону Ньютона, запишется так:

,

или

(38)

Это линейное дифференциальное уравнение второго порядка. Искомая функция — х, независимая переменная — t.

Характеристическое уравнение, если обозначить его неизвестное буквой s, будет таким:

;

.

Рассмотрим три случая: 1) h < k; 2) h = k; 3) h > k.

1) Если h<k, то . Обозначим . Тогда , а ; .

Общее решение:

или

При t = 0 имеем х₀ = С₁.

Найдем и определим С₂:

.

При t = 0

, или ,

.

Подставляя найденные значения C₁ и С₂ в общее решение, получим решение, удовлетворяющее начальным условиям:

.

Если обозначить

; (39)

то предыдущее равенство запишется так:

(40)

Возводя в квадрат обе части каждого из равенств (39) и складывая их почленно, получим

,

а .

Наличие в равенстве (39) множителя указывает на колебательный характер движения. С увеличением времени t множитель уменьшается и стремится к нулю. Когда время неограниченно возрастает, точка колеблется около начала координат, неограниченно к нему приближаясь. Движение в рассматриваемом случае является затухающим колебательным, а уравнение (38) называется уравнением затухающих колебаний.

2) Если h > k, то , ; корни характеристического уравнения s₁ и s₂ — числа вещественные и не равные между собой:

(41)

Из начальных условий следует, что

; .

Решение (41) описывает так называемый апериодический затухающий процесс движения точки к положению равновесия.

3) При h = k корни характеристического уравнения вещественны и между собою равны: s₁ = s₂ = — h:

(42)

; .

И в этом случае, когда , абсцисса движущейся точки , т.е. точка неограниченно приближается к началу координат положению равновесия, оставаясь с одной стороны от него, если начальная скорость v₀ не очень велика. Движение, описываемое уравнением (41), также называется апериодическим.

Теперь мы решим несколько линейных дифференциальных однородных уравнений порядка выше, чем второй с постоянными коэффициентами.

Задача 14. Найти решение уравнения

,

удовлетворяющее граничным условиям:

1) при ; 2) при ;

3) при ; 4) при (43)

Решение. Это уравнение встречается при решении задачи о потере устойчивости стержня, находящегося в магнитном поле. (Здесь EI — жесткость стержня; а — начальное расстояние между магнитом и стержнем; k — коэффициент пропорциональности; у — отклонение стержня от положения равновесия).

Из уравнения видно, что искомой функцией является у, а независимой переменной — z. Разделим обе части уравнения на EI и обозначим

; .

Уравнение переписывается так:

и представляет собой дифференциальное уравнение изогнутой оси стержня.

Характеристическое уравнение: . Разлагая его левую часть на множители, получаем:

, или .

Его корни: ; ; .Частные решения уравнения

; ; ; .

Общее решение:

.

Перепишем его в виде

Обозначим: ; , и для однообразности обозначений примем ; . Общее решение запишется теперь так:

(44)

Для определения четырех произвольных постоянных используем четыре заданных граничных условия (19,28) и получим систему уравнений:

(45)

Уравнения (45) представляют собой систему линейных однородных уравнений относительно неизвестных А₁, А₂, А₃, А₄. Как и всякая система алгебраических линейных однородных уравнений, она имеет тривиальное (самоочевидное) решение:

А₁= 0; А₂ = 0; А₃ = 0; А₄= 0.

Чтобы система (45) имела решение, отличное от нулевого необходимо и достаточно, чтобы определитель этой системы был равен нулю:

. (46)

Вычислим этот определитель. Отнимем от элементов четвертого столбца соответствующие элементы второго столбца, и уравнение (46) перепишется так:

.

Во второй строке все элементы, кроме второго, равны нулю, а поэтому определитель равен произведению этого неравного нулю элемента на его алгебраическое дополнение, и теперь уравнение (45) будет выглядеть так:

.

Вычислив определитель третьего порядка по известному правилу, получим уравнение

(47)

которое перепишем в виде

Построим график функций и (см. рис. 9). Абсциссы точек пересечения этих графиков и будут корнями этих уравнений. Наименьший корень al = = 1,873.

Установим теперь, какая зависимость существует между произвольными постоянным A₁, А₂, А₃, A₄.

Первое и второе уравнения системы (45) показывают, что

(48)

Исключая А₃ и A₄ из третьего и четвертого уравнений этой системы, получим:

. (49)

П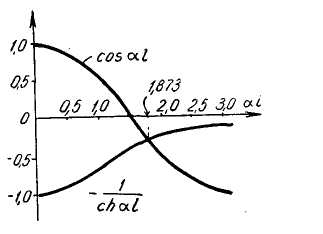 ервое уравнение системы дает

(50)

И, таким образом, все произвольные постоянные могут быть выражены через .

Рис. 9

Подставляя в (50) al = 1,873 и учитывая равенства (48), получаем:

; ;

а потому, так как общее решение (44) запишется так:

Окончательно, вынося А₁ за скобку, получим уравнение изогнутой оси стержня

содержащее единственный неопределенный параметр А₁ характеризующий масштаб кривой изгиба.

Замечание. Мы указали общий способ решения системы (45). Однако можно было бы и не идти этим общим путем, а исключить с помощью первого и второго уравнений этой системы неизвестные А₃ и А₄ и тем самым получить систему (49), из которой, приравнивая нулю ее определитель:

,

получили бы

.

Отсюда

, или ,

т. е. уравнение (47), которое было получено раньше.

Задача 15. Найти решение дифференциального уравнения

(51)

(s— постоянная величина), удовлетворяющее граничным условиям

1) при ; 2) при ; 3) у = 0 при ; 4) при .

Решение. К уравнению (51) приводит решение задачи об исследовании искривленной поверхности пластинки, жестко опертой по одной из ее длинных кромок и свободной вдоль другой, когда изгиб пластинки обусловлен аэродинамическими нагрузками. Величина s в уравнении зависит от скорости потока и от параметров пластинки.

Характеристическое уравнение: . Разлагая его левую часть на множители, получаем;

.

Корни:

Частные решения уравнения (51):

Общее решение:

(52)

Если использовать граничные условия, то для определения произвольных постоянных получим систему четырех однородных линейных алгебраических уравнений ,

необходимо и достаточно, чтобы определитель этой системы был равен нулю.

Однако мы не будем составлять этот определитель и вычислять его, а выразим, неизвестные С₃ и С₄ через С₂.

Из второго уравнения следует, что

С₄ = - С₂. (54)

Подставляя это значение С₄ в первое уравнение (53) получим

; ,

откуда

(55)

Теперь эти выражения С₄ и С₃ через С₂ подставим в четвертое уравнение и вынося за скобку С₂ , получим:

Так как по предположению , то

.

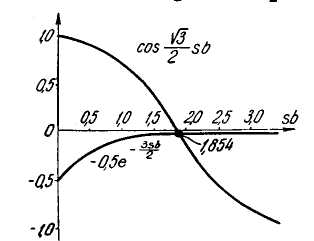Для определения параметра получаем уравнение

.

Рис. 10

Графическое решение этого трансцендентного уравнения дано на чертеже.

Точка пересечения этих кривых дает (см. рис. 10).

:

(53)

Для того, чтобы эта система уравнений имела решение, отличное от тривиального

;

Подставляя найденное значение в третье уравнение и используя соотношение (54) и (55), выразим С₁ через С₂:

;

;

, а поэтому

(56)

Подставляя (54), (55) и (56) в (52), получим решение, удовлетворяющее граничным условиям:

Это решение содержит один произвольный параметр С₂.

Задача 16(для самостоятельного решения).

Н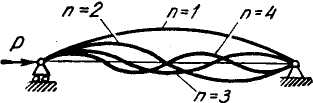 айти решение уравнения

,

Рис. 11

удовлетворяющее граничным условиям: .

Указание. К этому уравнению приводит задача о продольном изгибе стержня (задача Эйлера). Здесь Р — сила, сжимающая стержень вдоль его оси.

Обозначить

К задаче 19,14

Уравнение приводится к виду . Это дифферен­циальное уравнение изогнутой оси стержня при продольном изгибе. Его общее решение: . Из граничных условий получаем: из первого условия ; из второго условия, зная, что , имеем

,

отсюда или , или .

Если , то , т.е. решение тривиальное, которое, собственно, и искать было нечего. Остается рассмотреть . Отсюда ; , где п — любое целое число, не равное нулю. Так, если , то , , а этого не может быть.

Из ( ) следует, что , , . Подставляя эти значения в (А), получим ,

или (В)

Выражение (В) дает так называемое критическое значение сжимающей силы Р, действующей вдоль стержня, при котором становится возможным продольный изгиб.

Решение, удовлетворяющее граничным условиям, запишется так:

( )

При п = 1 сжимающая сила уравнение изогнутой оси стержня

.

Это основной случай.

Так как наибольшее значение , то и таким образом, С₂ есть не что иное, как наибольший прогиб стержня.

При п = 2 сила , а уравнение изогнутой оси стержня имеет вид ; и т. д.

Число п представляет собой число полуволн синусоиды, располагающихся по длине изогнутого стержня (см. рис.11).

Задача 17 (для самостоятельного решения).

Найти решение уравнения

,

удовлетворяющее граничным условиям:

1) при ; 2) при ; 3) при ; 4) при .

Указание. К предложенному уравнению сводится задача о статической неустойчивости трубопровода. Здесь EI — жесткость поперечного сечения трубопровода; q — вес жидкости, приходящейся на единицу длины трубопровода; g — ускорение силы тяжести; v — скорость потока жидкости; у — прогиб оси трубопровода.

Положить

(А)

Уравнение приобретает вид

.

Частные решения: ; ; ; .

Общее решение:

Из граничных условий окажется, что

; .

Первое значение , которое наиболее важно: ; .

Решение, удовлетворяющее граничным условиям:

Из (А) следует, что , и при получаем так называемое критическое значение скорости потока жидкости, при котором наступает потеря устойчивости прямолинейной формы равновесия трубопровода.

Задача 18. Весомая частица массы т брошена вертикально вверх и при движении испытывает сопротивление, пропорциональное первой степени скорости. Определить закон движения частицы, если в начальный момент t = 0 положение точки определяется координатой , а начальная скорость .

Решение. На точку действуют две силы: 1) сила тяжести Р, (g — ускорение силы тяжести) и 2) сила сопротивления , где через обозначен для удобства коэффициент пропорциональности.

Направим ось Ох, по которой происходит движение, вертикально вниз.

Уравнение движения будет таким:

(57)

где Р и f — соответственно модули силы тяжести и силы сопротивления.

Следует учесть, что сила сопротивления направлена всегда противоположно направлению движения, а скорость — в сторону движения. Модуль силы сопротивления

(A)

При движении частицы вверх проекция скорости отрицательна, т.е. , а модуль вектора всегда положителен. Поэтому в (А) при движении вверх надо взять знак минус. В этом случае угол между силой сопротивления и осью Ох равен 0°, вследствие чего , а произведение .

При движении частицы вниз проекция скорости . Для того, чтобы модуль силы был величиной положительной, надо в (А) взять знак плюс. В этом случае угол между силой сопротивления и осью Ох равен 180^е, а потому Рис. 12 , а произведение по-прежнему равно . Учитывая, что сила тяжести направлена вертикально вниз, ее модуль , угол между силой тяжести и осью Ох равен 0^е, , уравнение движения запишем так:

.

Сокращаем на т и переписываем уравнение в виде

(В)

Мы получили линейное неоднородное уравнение (искомая функция — х, независимая переменная — t, правая часть равна g).

Отбрасываем правую часть и находим общее решение соответствующего однородного уравнения

(С)

Его характеристическое уравнение: , .

(Конечно, буквой k здесь нельзя обозначать неизвестное характеристического уравнения, так как эта буква уже занята. Неизвестное характеристического уравнения мы обозначили буквой r).

Корни характеристического уравнения:

; (D)

Частные решения уравнения (В):

;

Его общее решение

. (Е)

Теперь определим частное решение неоднородного уравнения (В). Среди корней (D) характеристического уравнения нуль есть. Значит, число — корень характеристического уравнения простой (или однократный). Так как g — величина постоянная, многочлен нулевой степени, то надо P{х) и Q(х) считать многочленами нулевой степени и, следовательно, учитывая, что k = 1, искать частное решение неоднородного уравнения в виде X = At:

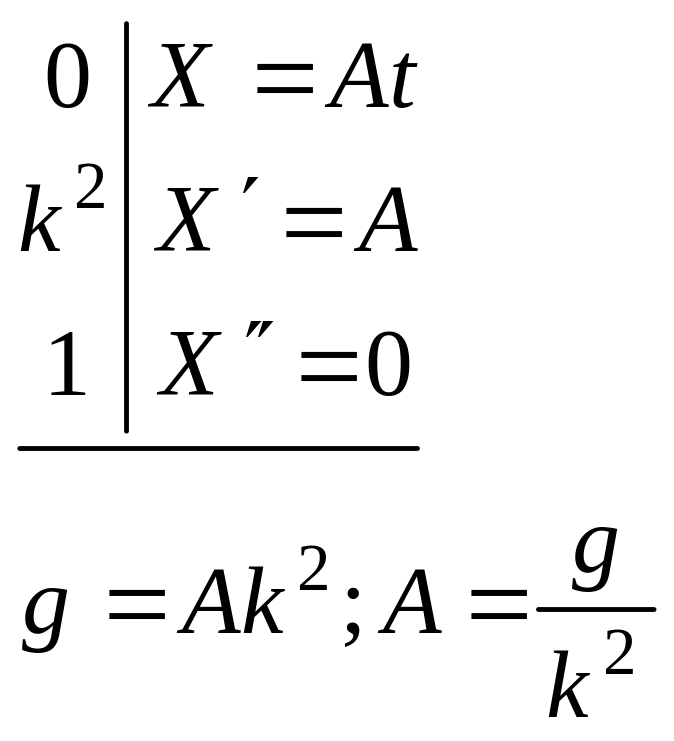
Поэтому ,а общее решение уравнения (В) будет равно сумме общего решения (Е) уравнения (С) и только что найденного частного решения неоднородного уравнения

. (F)

Теперь нам осталось из начальных условий определить произвольные постоянные С₁ и С₂. Подставляя и , получим

(G)

Продифференцируем обе части (F)

и поставим , а :

.

Отсюда

.

Подставляя это значение в (G), найдем

.

Найденные значения С₁ и С₂ подставим в (F) и получим окончательно решение, удовлетворяющее начальным условиям:

или

.

Из полученного результата можно сделать интересный вывод: если бы время t неограниченно возрастало, то , и тогда

,

т. е. движение асимптотически приближается к равномерному со скоростью

.

Положение точки при очень большом t мало отличалось бы от того, которое бы она занимала, двигаясь равномерно со скоростью , выйдя из начального положения, абсцисса которого равна .

Задача 19. Найти закон движения точки, на которую действуют две силы: 1) сила притяжения к неподвижному центру, пропорциональная расстоянию точки от этого центра (см. задачу 11), и 2) периодическая сила, определяемая формулой .

Решение. Дифференциальное уравнение движения будет таким:

.

Сократим уравнение на т и запишем его в виде

(А)

Уравнение — линейное неоднородное.

Рассмотреть следует два случая: 1) ; 2) р = k.

Уравнение (А) часто встречается в механике. Оно называется уравнением вынужденных колебаний при отсутствии сил сопротивления. Сила называется возмущающей.

Первый случай ( ). Отбросим в уравнении (А) правую часть и найдем общее решение уравнения

(В)

(уравнение свободных гармонических колебаний). Характеристическое уравнение имеет корни:

(С)

Общее его решение:

. (D)

Частное решение неоднородного уравнения (А) в случае, когда , следует искать учитывая, что = 0; β= р; +βi = pi не является корнем характеристического уравнения:

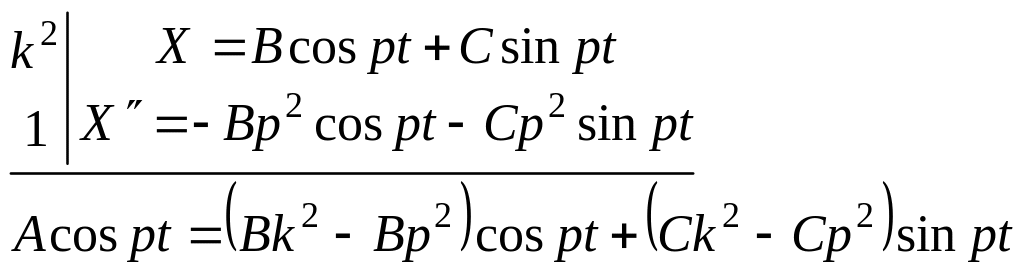
Сравнивая коэффициенты при и , получаем уравнения для определения неизвестных коэффициентов В и С:

.

Поэтому

; ;

(так как , то ).

Общее решение уравнения (А) в этом случае будет таким:

(E)

Второй случай (р = k). В этом случае по-прежнему  = 0; β= р, но так как р = k, то β= k, а число +βi = ki является корнем характеристического уравнения (см. (С) только не упустить из вида, что независимую переменную х надо заменить на t). Правая часть заданного уравнения теперь равна (p заменено буквой k).

Итак, частное решение в этом случае:

Сравнивая коэффициенты при и в левой и правой частях этого равенства, получаем

; ;

частное решение неоднородного уравнения потому общее решение уравнения вынужденных колебаний (А) при р = k (это уравнение полезно запомнить) запишется так:

.

Рассмотренный второй случай представляет особый интерес. Наличие множителя t в последнем слагаемом указывает на то, что с возрастанием времени t абсцисса х точки (т. е. ее размахи) неограниченно увеличивается и может достигнуть сколь угодно большой величины. Это явление называется резонансом. Оно наступает тогда, когда частота возмущающей силы равна частоте свободных колебаний точки (р = k). Следует обратить внимание на то, что при отсутствии возмущающей силы движение описывалось бы уравнением (В), а закон движения — уравнением (D) и точка совершала бы свободные гармонические колебания (см. задачу 10). Уже рассмотрение решения (Е) показывает, что, когда частоты свободных и вынужденных колебаний (числа р и k) мало отличаются одна от другой, знаменатель в последнем слагаемом мал, а само оно становится большим.

Из сказанного ясно, что при проектировании сооружений, судов, машин, фундаментов и т. д. надо всячески избегать явления резонанса, т. е. не допускать совпадения частот собственных колебаний с частотой накладывающейся возмущающей силы. Устранение этого явления может быть достигнуто увеличением разности между этими частотами.

Задача 20. При изучении предмета «Сопротивление материалов» приходится решать так называемую задачу Ляме об определении напряжений в точках толстостенной цилиндрической трубы по известным равномерно распределенным давлениям, действующим на ее внутреннюю и наружную поверхности. Решение задачи приводит к дифференциальному уравнению

,

которое является уравнением Эйлера.

Проинтегрируйте его самостоятельно.

Ответ. .

Задача 21. Найти решение системы

,

удовлетворяющее начальным условиям: ; ; (k и g—постоянные величины).

Решение. Предложенная система уравнений описывает движение снаряда с учетом сопротивления среды.

Каждое из уравнений системы содержит только одну неизвестную функцию.

Из первого уравнения следует

.

Характеристическое уравнение имеет корни: ; . Частные решения уравнения: ; . Его общее решение

(A)

Чтобы определить С₁ и С₂, найдем

(В)

При t = 0 имеем:

из (А) ;

из (В) .

Отсюда ; .

Подставляя эти значения С₁ и.С₂ в (А), получим

. (1)

Второе уравнение перепишем так:

. (С)

Уравнение линейное неоднородное. Общее решение соответствующего однородного уравнения:

.

Так как корни характеристического уравнения — числа 0 и –k  = β= 0, а число  + βi =0 является корнем характеристического, то частное решение следует искать в виде:

Общее решение уравнения (С):

. (D)

Для определения С₃ и С₄ из начальных условий найдем у':

(E)

Учитывая начальные условия, получаем систему уравнений:

из (D) ;

из (Е) ;

; .

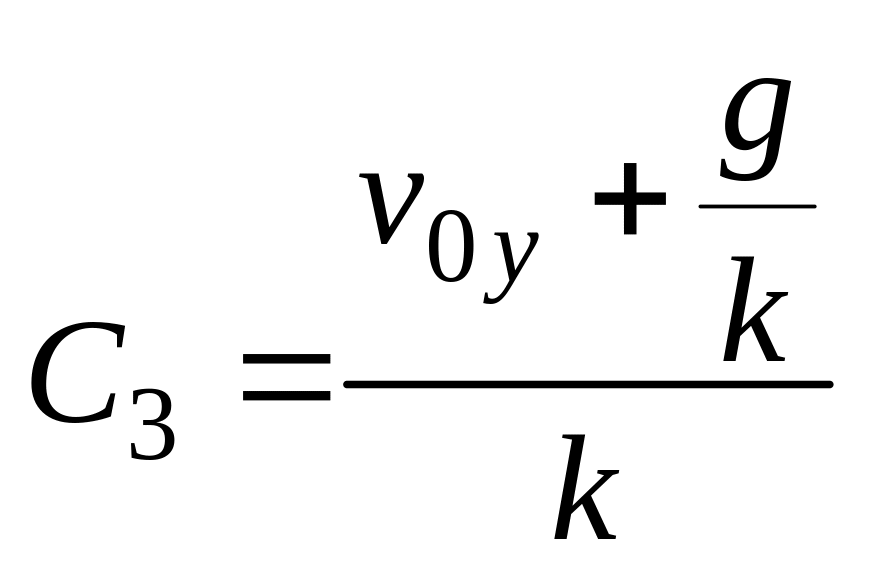Подставляя эти значения С₃ и С₄ в (D), получим

(2)

Уравнения (1) и (2) являются параметрическими уравнениями траектории снаряда.

Исключите самостоятельно параметр t из этих уравнений (из (1) выразить t через х и подставить в (1)). Окажется, что

.

Из последнего уравнения можно определить горизонтальную дальность стрельбы, если положить в нем у = 0, и из полученного уравнения найти х.