6.1. Геометрические задачи, приводящие к решению дифференциальных уравнений 1-го порядка

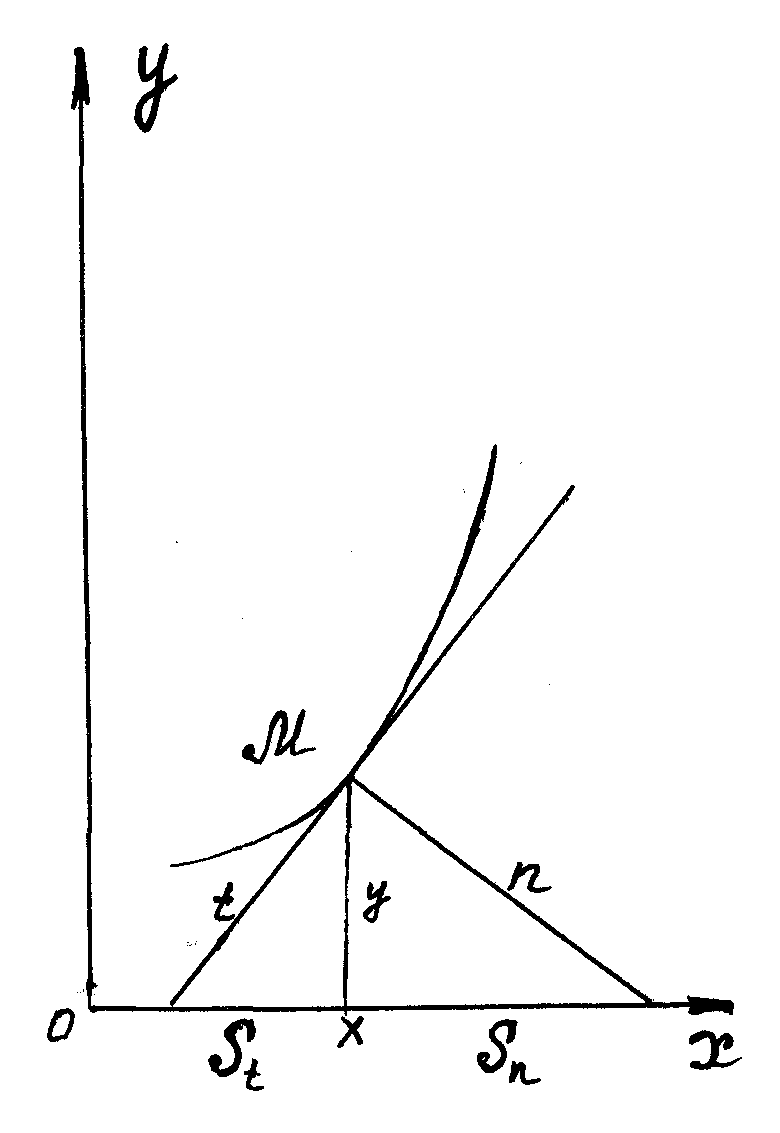
В задачах геометрии, в которых требуется найти уравнение кривой по заданному свойству ее касательной, нормали или площади криволинейной трапеции, используется геометрическое истолкование производной (угловой коэффициент касательной) и следующие общие формулы для определения длин отрезков касательной t, нормали n, подкасательной S_t и поднормали S_n (рис.2.):

Рис. 2.

Касательная t, нормаль n, подкасательная S_t и поднормаль S_n

При решении таких задач с помощью дифференциальных уравнений рекомендуется следующая последовательность действий:

1. выполнить чертеж и ввести обозначения;

2. отделить условия, имеющие место в произвольной точке искомой линии, от условий, выполняющихся лишь в отдельных точках (начальных условиях);

3. выразить все упомянутые в задаче величины через координаты произвольной точки и через значения производной;

4. по условию задачи составить дифференциальное уравнение, для которого искомая кривая является интегральной кривой.

Задача№9. Найти линию, проходящую через точку M₀(e, 0), и обладающую тем свойством, что в любой ее точке M касательный вектор с концом на оси OY имеет проекцию на ось OY, равную a=1.

Р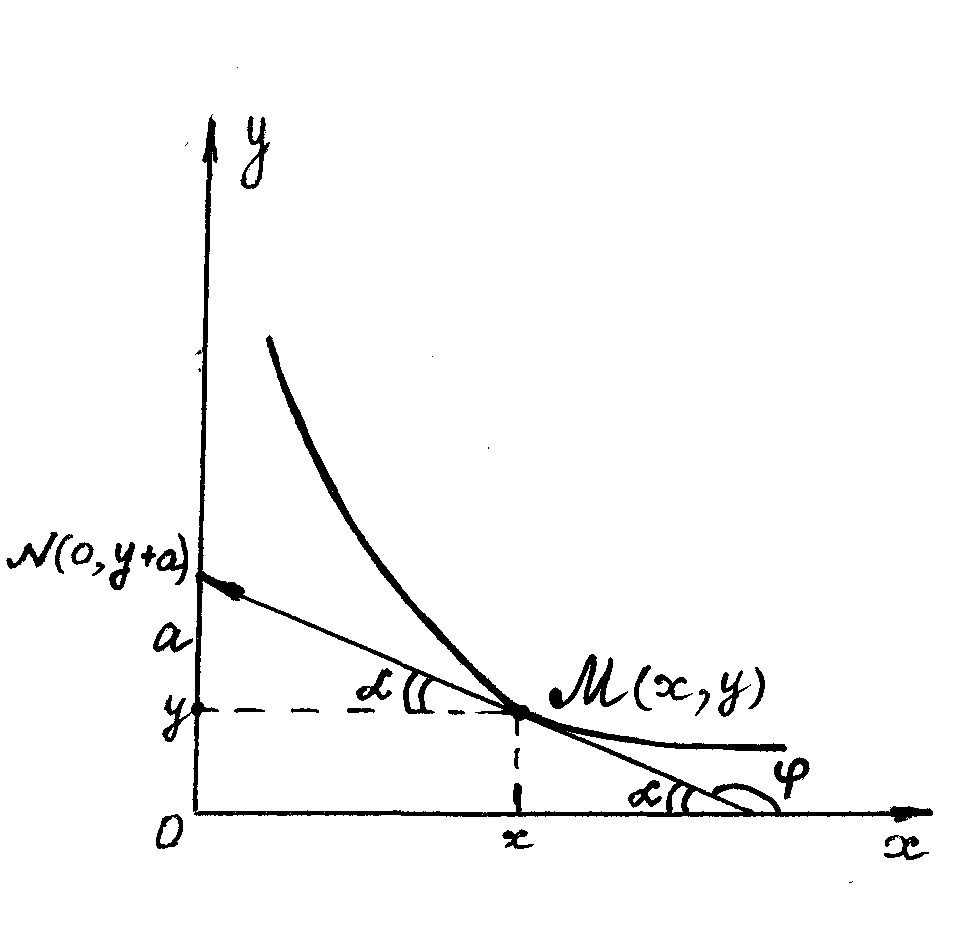 ешение. Ищем функцию y=y(x). Воспользуемся геометрическим свойством производной: представляет угловой коэффициент касательной к графику этой функции (с положительным направлением оси OX), т.е. .

Рис. 3

Найдем :

.

С другой стороны (из треугольника AMN): . Тогда .

Решая это уравнение, найдем, что .

Подставим M₀(e;0) и a=1: 0=-1+c, отсюда c=1. Тогда линия, проходящая через точку M₀ удовлетворяющая условиям нашей задачи, будет иметь вид

.

7. Дифференциальные уравнения высших порядков, допускающие понижение порядка

7. 1. Первый тип. Уравнения, содержащие только производную порядка n и независимую переменную

Это уравнения вида . Если удается разделить их относительно , то . Общее решение последнего уравнения имеет вид:

.

Т.е. решение получается путем n-кратного интегрирования.

7. 2. Второй тип. Уравнения, не содержащие искомой функции

Такое уравнение имеет вид: . Порядок его может быть понижен с помощью подстановки: , где - новая искомая функция.

Если уравнение имеет вид , то подстановка понижает порядок на k единиц.

7. 3. Третий тип. Уравнения, не содержащие независимой переменной

.

Понижение порядка на единицу достигается подстановкой , где — новая искомая функция.

Частный случай. Если уравнение имеет вид , и его удается решить относительно так, что , то интегрирование можно привести так. Умножим обе части на :

.

Т.к. и , то . Отсюда,

и

.

Задача №10. Найти общее решение дифференциального уравнения .

Решение. Имеем неоднородное дифференциальное уравнение второго порядка не содержащее искомой функции y. Порядок его может быть понижен с помощью подстановки , где - новая искомая функция. Эта подстановка приводит к уравнению:

.

Это линейное уравнение относительно z и . Разделим его обе части на коэффициент при и получим

.

Решением этого уравнения является функция . (Способы решения см. в задаче№4). Но , а потому .

Пришли к случаю, когда уравнение содержит только производную и независимую переменную, т.е. . Такие уравнения решаются путем интегрирования n-раз обеих частей уравнения, причем общее решение должно содержать в себе n констант. В нашем случае n=1.

— общее решение.

Уравнение действительных решений не имеет, поэтому нет и особых решений.

Задача №11. Найти решение задачи Коши.

.

Решение. Уравнение не содержит независимой переменной x. Понижение порядка на единицу достигается подстановкой , где P(y) – новая искомая функция.

Уравнение перепишется так:

Тогда . Но .

Для облегчения решения этого уравнения найдем c_1, воспользовавшись начальными условиями, т.е. . Подставляя их в последнее уравнение, получим c₁=0.

Тогда — уравнение с разделяющимися переменными, решением которого будет .

Подставляя начальные условия, установим, что .

Ответ. .

Существует и второй способ решения этого уравнения. Если разрешить его относительно , т.е. и умножить обе части на , то

.

Левая часть этого уравнения ,а в правой — , поэтому последнее уравнение перепишется так:

.

Отсюда следует, что

.

Последнее уравнение допускает разделение переменных. Предварительно с помощью начальных условий можно установить, что c₁=0, а . С помощью начальных условий найдем, что . Таким образом, пришли к тому же результату, что и в I способе.