5.5.1.1. Кинетика кислотного катализа.

Решение кинетической задачи рассмотрим на примере реакций специфического кислотного⁵ катализа.

Пусть взаимодействие субстрата (S) и катализатора (H₃O⁺) протекает по схеме:

равновесная стадия процесса

лимитирующая стадия

Скорость лимитирующей стадии определяет скорость протекания процесса:

v = k₂ c_SH⁺, (5.23)

где k₂ = k^’₂·c

Концентрация протонизированного субстрата (c _SH⁺) составляет какую–то долю (α) от исходной концентрации субстрата (c_S⁰):

α = c_SH⁺/c_S⁰ или c_SH⁺ = α· c_S⁰. (5.24)

Учитывая это, уравнение для скорости лимитирующей стадии будет равно:

v = k₂ α· c_S⁰. (5.25)

Степень протонизации субстрата (α) можно оценить из константы равновесия первой стадии процесса:

, или (5.26)

Откуда

или (5.27)

где – кислотность среды.

Преобразуем уравнение (5.27), используя свойство дробей:

(5.28)

Так как , то степень протонизации субстрата α равна:

(5.29)

Подставляя уравнение (5.29) в (5.25) получим выражение для скорости лимитирующей стадии процесса:

, (5.30)

Как видно из уравнения (5.30), определяемая из опытных данных эффективная константа скорости зависит от кислотности среды:

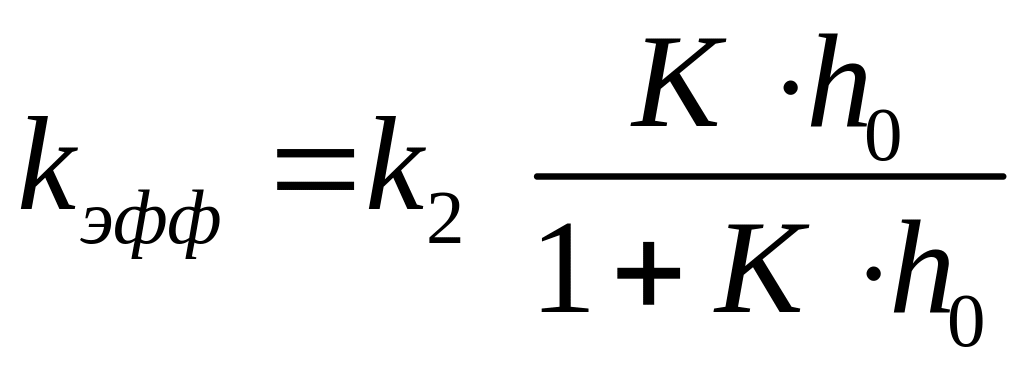(5.31)

Проведем анализ уравнения (5.31).

1. Если равновесие первой стадии устанавливается быстро, то константа равновесия К достаточно большая величина по сравнению с 1, тогда .

2. Если равновесие первой стадии устанавливается медленно, то константа равновесия (К) маленькая величина и слагаемым К·h₀ в знаменателе можно пренебречь. В этом случае уравнение (5.31) имеет вид:

.

После логарифмирования имеем:

, (5.32)

где – функция кислотности.

Построив по экспериментальным данным график в координатах lgk_эфф – рН, можно оценить значение произведения k₂·K. Если известна константа равновесия первой стадии, то можно определить k₂.·

3. Если константа равновесия К – средняя величина, то уравнение (5.31) можно привести к виду прямой линии:

(5.33)

График, построенный по опытным данным в координатах , в случае соответствия этой модели реальной кинетике процесса должен изображаться прямой линией. Зная угловой коэффициент прямой и отрезок на оси ординат, можно вычислить и К.

5.5.1.2. Кинетика основного катализа

Решение кинетической задачи рассмотрим на примере реакций специфического основного катализа.

Пусть взаимодействие протонизированного субстрата (SН) и катализатора (ОH^–, Н₂O, Cl^–) протекает следующим образом:

,

,

.

Каждая из этих стадий может лимитировать скорость протекания всего процесса.

Заключительные стадии процесса являются равновесными, так как протекают значительно быстрее:

,

,

.

Таким образом, протонизированный субстрат (SH) взаимодействует с тремя разными катализаторами (параллельные химические реакции), поэтому скорость его расходования будет равна сумме скоростей на отдельных стадиях:

v_SH = v₁+ v₂+ v₃

или

v_SH= , (5.34)

где

(5.35)

Кажущаяся константа скорости определяется из экспериментальных данных. Изучая, как эта константа меняется от можно оценить каждую из каталитических констант: .