3. Соотношения линейности Бренстеда-Поляни в катализе

Перспективный подход к предвидению каталитического действия твердых катализаторов основан на использовании соотношения линейности Бренстеда-Поляни, суть и основное значение которого состоит в том, что оно устанавливает связь между кинетическими (Е, k, ) и термодинамическими (   ) величинами, характерными для данного каталитического процесса.

Разные формы этого соотношения имеют вид:

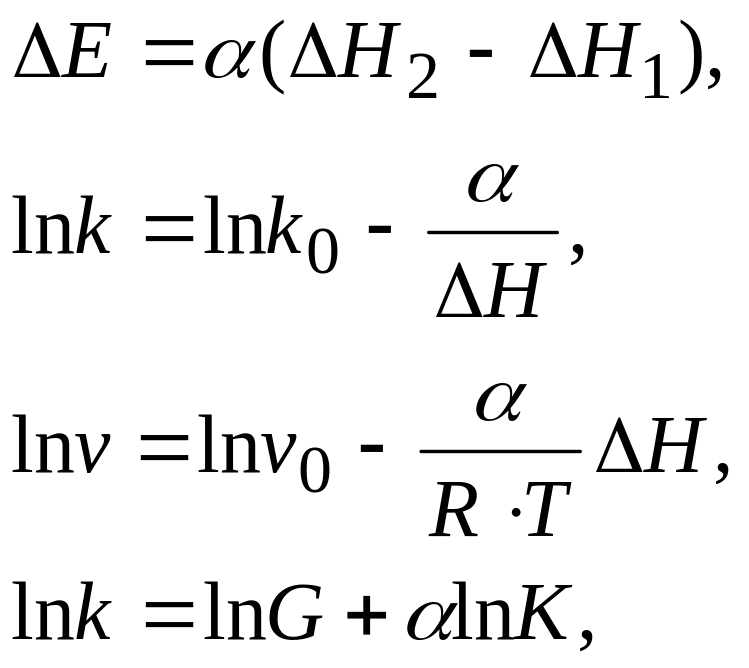(5.12)

где , lnk₀, lnv₀ – постоянные эмпирические коэффициенты в ряду сходных катализаторов для данной реакции и в ряду однотипных реакций для данного катализатора; k, v – константа скорости и скорость реакции, К –константа равновесия, G – энергия Гиббса.

Тепловой эффект реакции () и энергия Гиббса (G) отражают величину энергии разрыва связи катализатор-субстрат.

Рассмотрим для примера реакцию окисления на оксидах металлов в качестве катализатора. Соотношение Бренстеда-Поляни используется в форме:

Е = Е⁰ +  , (5.13)

где Е⁰ и  – постоянные, одинаковые в ряду разных оксидов для заданной реакции окисления. Энергия активации реакции для разных катализаторов (Е) и теплота адсорбции кислорода на катализаторе ( ) (равная энергии связи кислорода (Q) с металлом).

Строится график в координатах Е – , определяется  и Е⁰, зная которые можно рассчитать Е по известному или наоборот для катализаторов, с которыми не проводились опыты. По этим величинам можно судить об активности катализаторов. Корреляция между каталитической активностью и энергией связи кислорода справедлива не только для простых оксидов, но и для более сложных соединений типа шпинелей, солей ванадатов, молибдатов, смешанных оксидов и т.д.

Вопросы для самоконтроля

1. Что является мерой каталитической активности в гомогенном и ферментативном катализе? Каков порядок этой величины в каждом из типов катализа?

2. Какие величины используют для оценки эффективности катализатора в гетерогенном катализе?

3. В чем различие терминов «интегральная» и «дифференциальная» селективность? Ответ поясните.

4. Во сколько раз увеличиться скорость химической реакции при изменении активационного барьера на: а) 4 кДж/моль;б) 40 кДж/моль.

5.4 Механизмы гомогенных каталитических реакций

Промежуточное химическое взаимодействие реагентов с катализатором может протекать по двум видам механизма – слитно и раздельно.

При слитном механизме с состав активированного комплекса (промежуточного соединения) входят, наряду с катализатором, все реагирующие вещества и реакция идёт по схеме:

1. A + B  AB  D + E без катализатора,

2. A + B +K ABK  D + E + K c катализатором.

Увеличение скорости реакции в этом случае объясняется уменьшением энергии активации процесса

При раздельном механизме каталитический процесс осуществляется поэтапно:

3. .

4. .

Все соединения со значком ( ) означают активированный комплекс системы, находящейся в переходном состоянии. В этих реакциях суммарная энергия активации реакции необязательно должна уменьшаться, а скорость процесса растёт за счёт роста энтропийного фактора, так как при этом растёт количество стадий и упрощается строение активированных комплексов. Реакции с раздельным и слитным механизмом протекают при разных температурах; первые – при 600 – 800 К, а вторые – в области 300 - 400 К.

Как правило, катализатор снижает энергию активации реакции и ускоряет её. Замедлить реакцию (не цепную) катализатор не может, так как если в присутствии катализатора энергия активации растёт, то реакция пойдёт по обычному, не каталитическому пути и скорость её окажется прежней. Замедляющее действие катализатор может оказывать на цепную реакцию, когда он ускоряет стадию обрыва цепи.

Рассмотрим реакцию, протекающую по раздельному механизму [см. уравнения (3), (4)]. Согласно теории активированного комплекса, скорость реакции определяется скоростью распада комплекса на конечные продукты:

. (5.14)

В соответствии с принципом стационарности:

. (5.15)

Откуда:

, (6.16)

, (5.17)

. (5.18)

Подставляя (5.18) в (5.16) и затем в (5.14), находим:

. (5.19)

Это уравнение лежит в основе кинетики гетерогенно–каталитических реакций.

Из (5.19) видно, что скорость образования продукта реакции прямо пропорциональна концентрации катализатора с_К, что хорошо согласуется с опытом.

Характерные частные случаи:

1) если k₂k₃, т.е. константа скорости распада промежуточного соединения АК на исходные реагенты значительно превышает константу скорости образования активированного комплекса AKB , то

, (5.20)

т.е. скорость реакции прямо пропорциональна концентрации катализатора и реагентов. Промежуточное вещество (АК) называется промежуточным веществом Аррениуса.

2) если k₂  k₃ , тогда всё количество промежуточного вещества превращается в конечные продукты и скорость реакции пропорциональна концентрации вещества (A), из которого образуется вещество (АК):

. (5.21)

Промежуточное вещество в этом случае носит название промежуточное вещество Вант Гоффа. Например, реакция окисления тиосульфата перекисью водорода в кислой среде с I^– ионами

2S₂O₃^2- + H₂O₂ + 2H⁺  S₄O₆^2- + 2H₂O

идёт по стадиям:

I^– + H₂O₂  IO^- + H₂O,

I^-+ IO^– + 2H⁺  I₂ + H₂O,

I₂ + 2S₂O₃^2–  S₄O₆^2– + 2I^–.

В этом случае IO^– – промежуточное вещество Вант Гоффа. Если же в качестве катализатора взять молибденовую кислоту, то конечным продуктом её будут сульфат ионы и вода:

MoO₄ + 4H₂O₂  [MoO₈]^2– + 4H₂O,

[MoO₈]^2– + S₂O₃^2– +H₂O  2SO₄^2– + 2H⁺ + [MoO₄]^2–,

причём [MoO₈]^2– – является промежуточным веществом Аррениуса.