
- •Линейная алгебра.
- •Основные действия над матрицами.
- •Определители.
- •Матричный метод решения систем линейных уравнений.
- •Метод Крамера.
- •Элементарные преобразования систем.
- •Метод Гаусса.
- •Векторная алгебра и аналитическая геометрия. Элементы векторной алгебры.
- •Линейная зависимость векторов.
- •Скалярное произведение векторов.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •Комплексные числа.
- •Тригонометрическая форма числа.
- •Действия с комплексными числами.
- •Предел функции в точке.
- •Предел функции при стремлении аргумента к бесконечности.
- •Основные теоремы о пределах.
- •Бесконечно малые функции.
- •Бесконечно большие функции и их связь с бесконечно малыми.
- •Некоторые замечательные пределы.
- •Вычисление пределов.
- •Непрерывность функции в точке.
- •Точки разрыва и их классификация.
- •Формула Тейлора.
- •Формула Маклорена.
- •Представление некоторых элементарных функций по формуле Маклорена.
- •Правило Лопиталя.
- •Производные и дифференциалы высших порядков.
- •Возрастание и убывание функций.
- •Точки экстремума.
- •Исследование функции на экстремум с помощью производных высших порядков.
- •Выпуклость и вогнутость кривой. Точки перегиба.
- •Асимптоты.
Векторное произведение векторов.
Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:
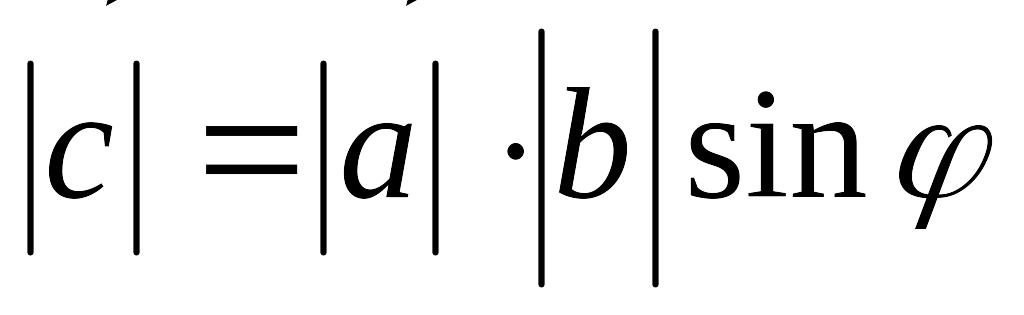 ,
где - угол между
векторами
и
,
,
где - угол между
векторами
и
,
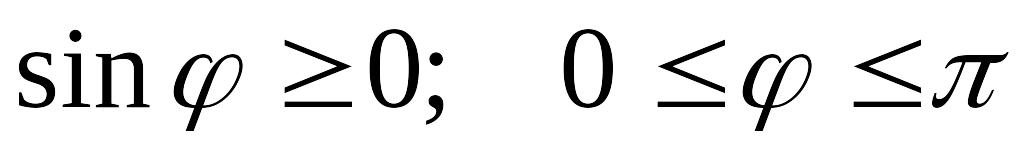
вектор ортогонален векторам и
, и образуют правую тройку векторов.
Обозначается:
![]() или
или![]() .
.

Свойства векторного произведения векторов:
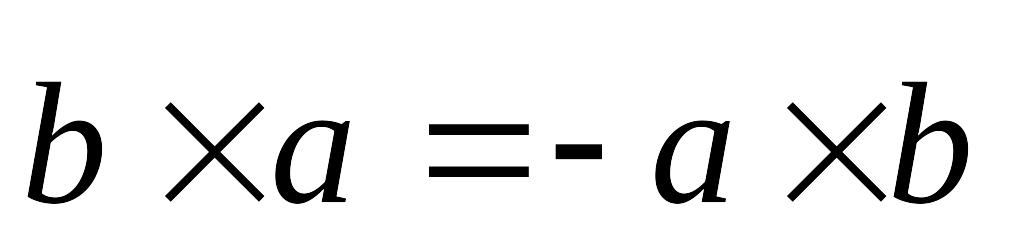 ;
;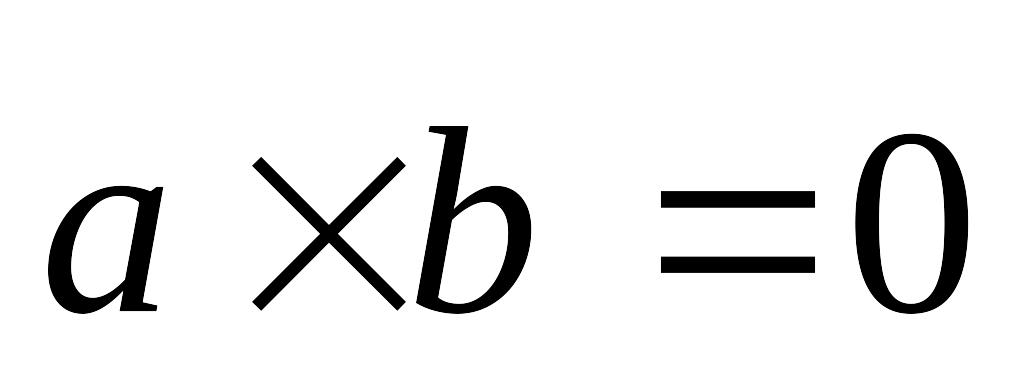 ,
если
или
=
0 или
=
0;
,
если
или
=
0 или
=
0;Если заданы векторы
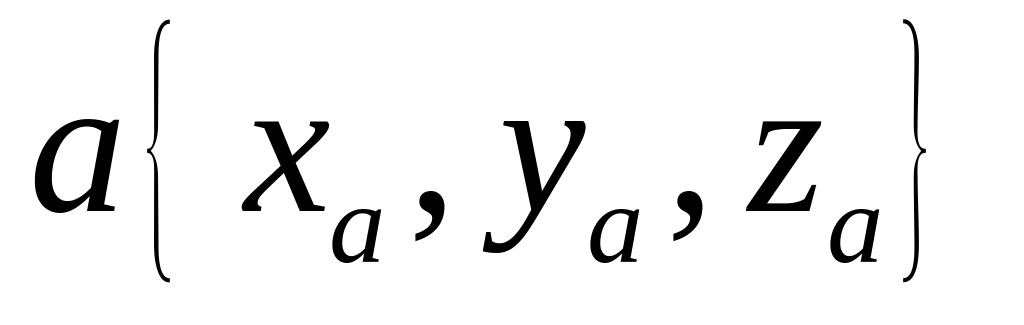 и
и
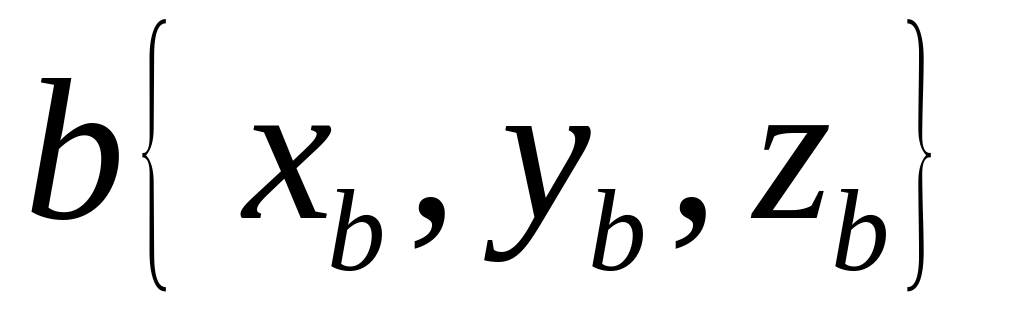 в декартовой прямоугольной системе
координат с единичными векторами
в декартовой прямоугольной системе
координат с единичными векторами
 ,
то
,
то
=
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .
Пример. Найти
векторное произведение векторов
![]() и
и
![]() .
.
= (2, 5, 1); = (1, 2, -3)
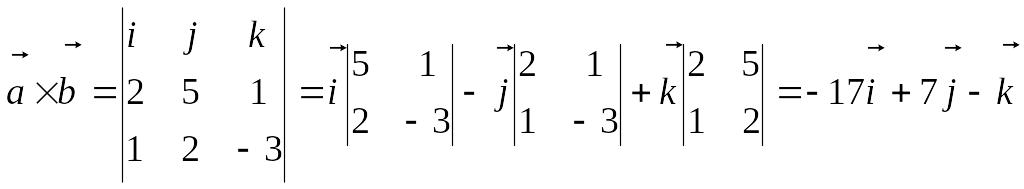
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
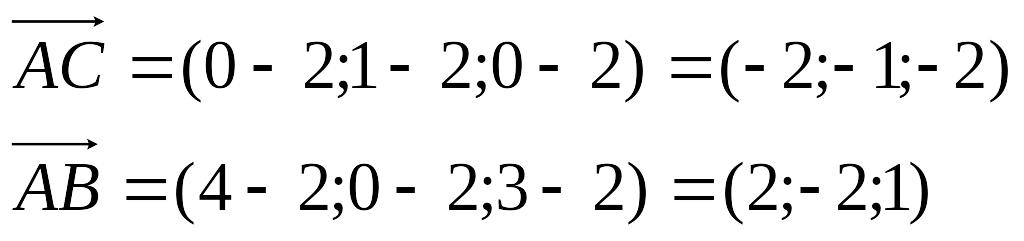
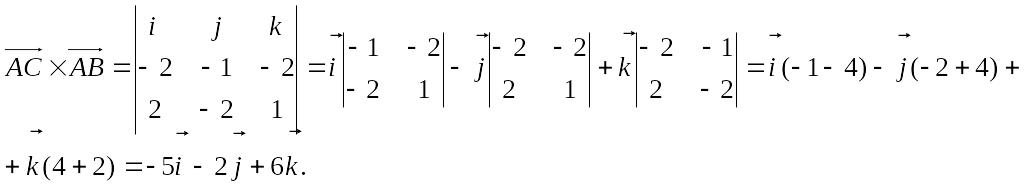
![]()
![]() (ед2).
(ед2).
Смешанное произведение векторов.
Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .
Обозначается
![]() или
(
,
,
).
или
(
,
,
).
Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .
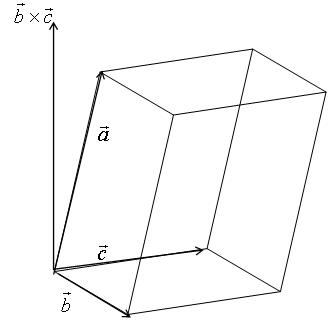
Объем треугольной пирамиды, образованной векторами , и , равен
![]()
Если
![]() ,
,
![]() ,
то
,
то
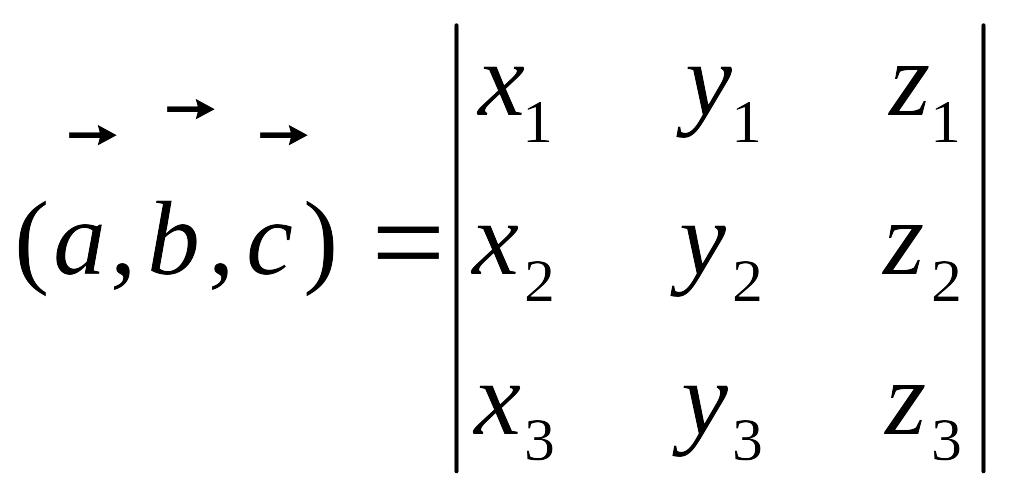
Пример. Найти объем пирамиды, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов:
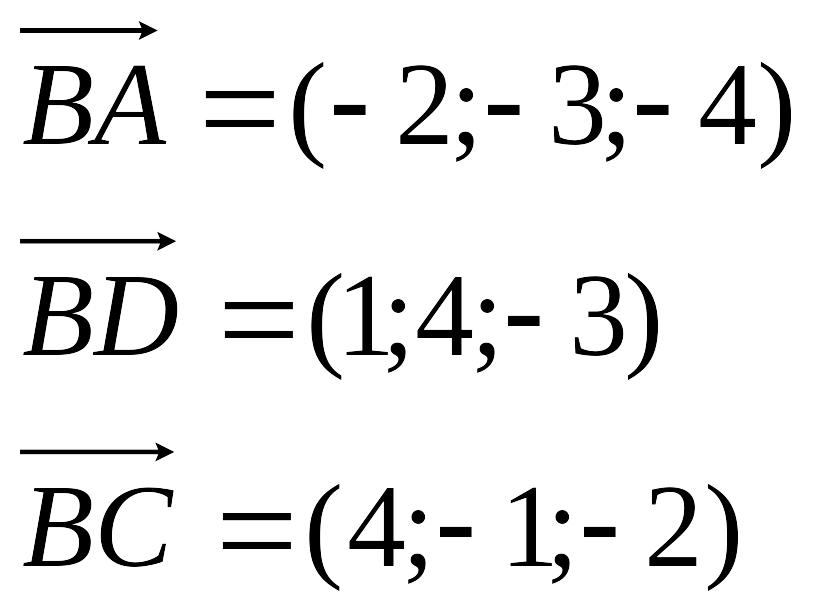
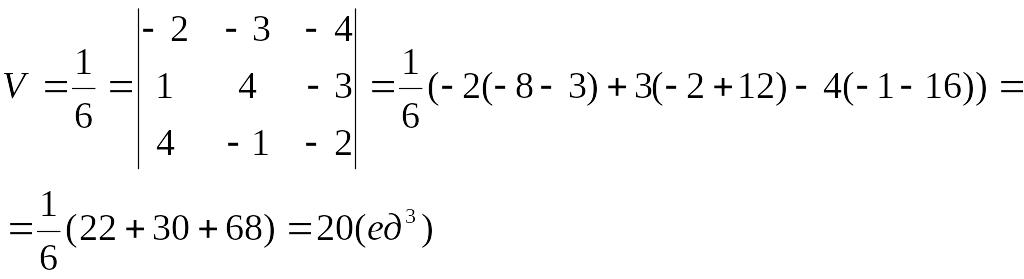
Общее уравнение плоскости.
Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты
вектора
![]() -вектор
нормали к плоскости.
-вектор
нормали к плоскости.
Уравнение плоскости, проходящей через три точки.
Для того, чтобы через три какие-либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.
Уравнение плоскости, проходящей через три точки:
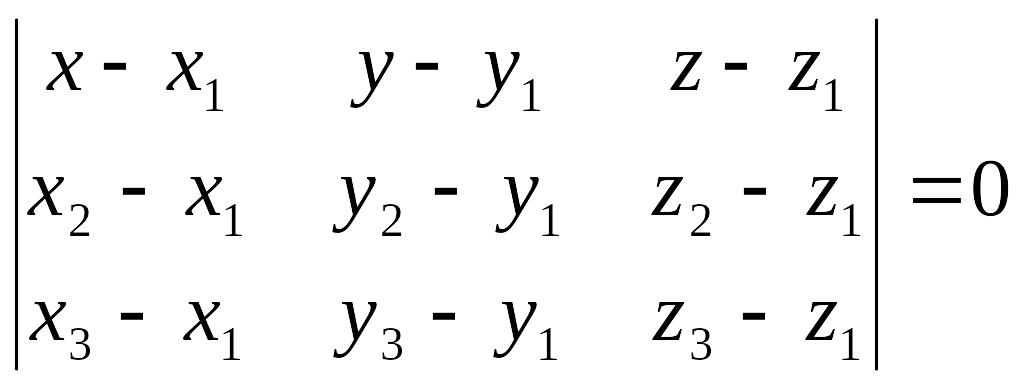
Уравнение плоскости в отрезках.
Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на -D
![]() ,
,
заменив
![]() ,
получим уравнение плоскости в отрезках:
,
получим уравнение плоскости в отрезках:
![]()
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.
Расстояние от точки до плоскости.
Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
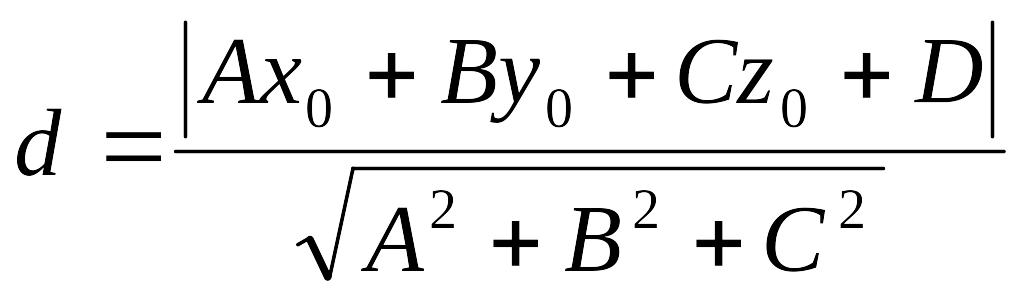
Уравнение прямой на плоскости.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M1(x1, y1) и M2(x2, y2), тогда уравнение прямой, проходящей через эти точки:
![]()
Уравнение прямой с угловым коэффициентом.
![]()
Уравнение прямой в отрезках.
![]() ,
,
Геометрический смысл
коэффициентов в том, что коэффициент
![]() является координатой точки пересечения
прямой с осью Ох, а b – координатой точки
пересечения прямой с осью Оу.
является координатой точки пересечения
прямой с осью Ох, а b – координатой точки
пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
![]() ,
а = -1, b = 1.
,
а = -1, b = 1.
Угол между прямыми на плоскости.
Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
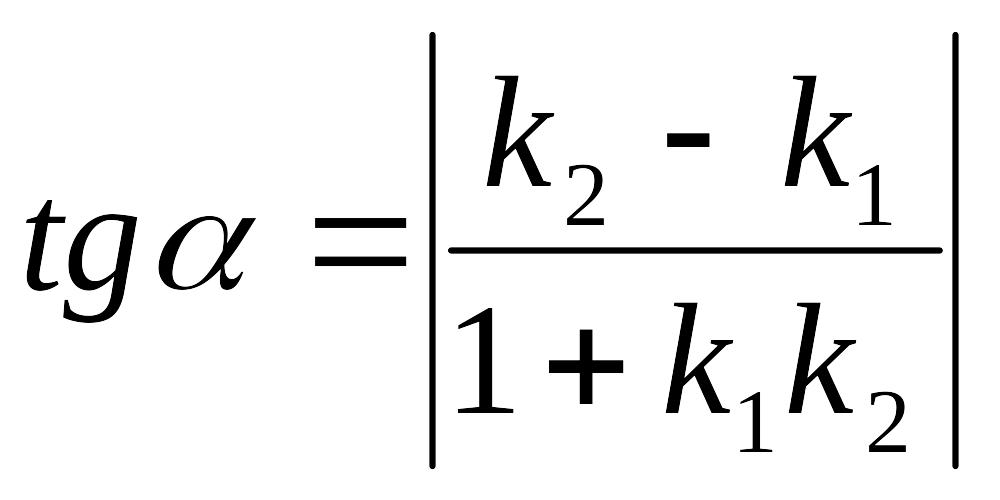 .
.
Две прямые параллельны, если k1 = k2.
Две прямые перпендикулярны, если k1 = -1/k2.
Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
K1 = -3; k2 = 2 tg
=
![]() ;
= /4.
;
= /4.
Расстояние от точки до прямой.
Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
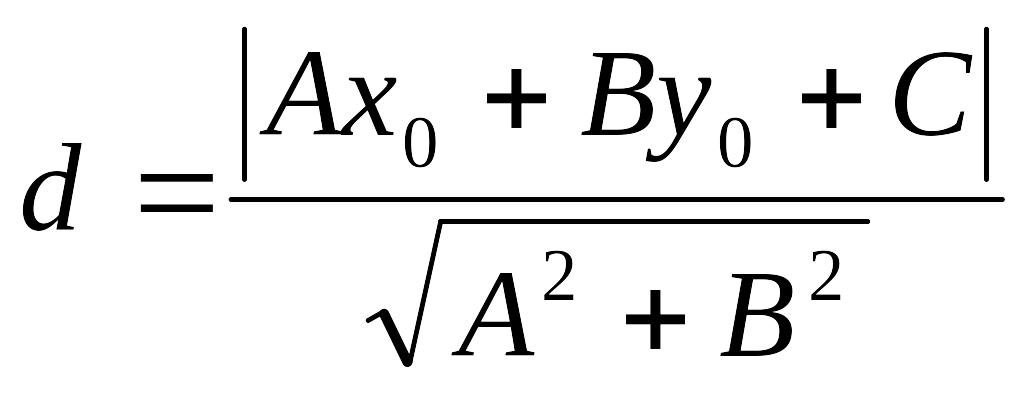 .
.
Кривые второго порядка.
![]() - уравнение эллипса.
- уравнение эллипса.
![]() - уравнение гиперболы.
- уравнение гиперболы.
![]() – уравнение параболы.
– уравнение параболы.
![]() –
уравнение окружности радиуса
–
уравнение окружности радиуса
![]() с центром в точке
с центром в точке
![]() .
.
Уравнение линии в пространстве.
Пусть F(x, y, z)=0 и Ф(x, y, z)=0 – уравнения поверхностей, пересекающихся по линии L.
Тогда пара уравнений
![]()
называется уравнением линии в пространстве.
Угол между плоскостями.
Таким образом, угол между плоскостями находится по формуле:
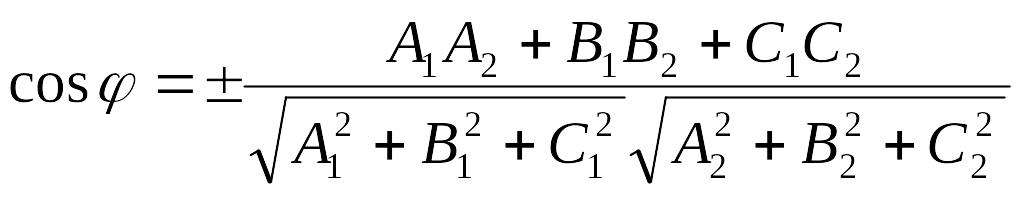
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Условия параллельности и перпендикулярности плоскостей.
плоскости перпендикулярны,
если:
![]() .
.
Плоскости параллельны,
если:
![]() .
.
Полярная система координат.
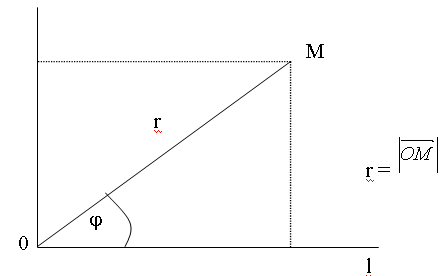
Точка О называется полюсом, а луч l – полярной осью.
угол называется полярным углом.
Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:
x = rcos;
y = rsin;
![]()
Цилиндрическая и сферическая системы координат.
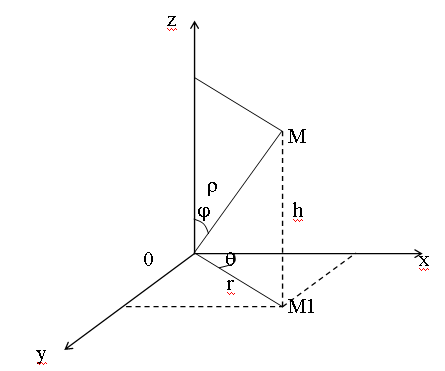
![]() ОМ1 = r; MM1 = h;
ОМ1 = r; MM1 = h;
Если из точки М опустить перпендикуляр ММ1 на плоскость, то точка М1 будет иметь на плоскости полярные координаты (r, ).
Цилиндрическими координатами точки М называются числа (r, , h), которые определяют положение точки М в пространстве.
Сферическими координатами точки М называются числа (r,,), где - угол между и нормалью.
Связь цилиндрической и декартовой прямоугольной системами координат:
h = z; x = rcos; y = rsin;
cos
=
![]() ;
sin =
;
sin =
![]() .
.
Связь сферической системы координат с декартовой прямоугольной:
![]()

