Титова Галина Владимировна avergv@mail.ru.

Линейная алгебра. 3

Векторная алгебра и аналитическая геометрия. 8

Комплексные числа. 16

Математический анализ. 18

Дифференциальное исчисление функции одной переменной 26

Линейная алгебра. 3

Основные действия над матрицами. 3

Определители. 4

Матричный метод решения систем линейных уравнений. 5

Метод Крамера. 6

Элементарные преобразования систем. 7

Метод Гаусса. 7

Векторная алгебра и аналитическая геометрия. 8

Элементы векторной алгебры. 8

Линейная зависимость векторов. 9

Скалярное произведение векторов. 10

Векторное произведение векторов. 11

Смешанное произведение векторов. 12

Общее уравнение плоскости. 13

Уравнение плоскости, проходящей через три точки. 13

Уравнение плоскости в отрезках. 13

Расстояние от точки до плоскости. 13

Уравнение прямой на плоскости. 14

Уравнение прямой, проходящей через две точки. 14

Уравнение прямой с угловым коэффициентом. 14

Уравнение прямой в отрезках. 14

Угол между прямыми на плоскости. 14

Расстояние от точки до прямой. 14

Кривые второго порядка. 15

Уравнение линии в пространстве. 15

Угол между плоскостями. 15

Условия параллельности и перпендикулярности плоскостей. 15

Полярная система координат. 15

Цилиндрическая и сферическая системы координат. 16

Комплексные числа. 16

Тригонометрическая форма числа. 17

Действия с комплексными числами. 17

Показательная форма комплексного числа. 18

Математический анализ. 18

Числовая последовательность. 18

Ограниченные и неограниченные последовательности. 18

Предел функции в точке. 19

Предел функции при стремлении аргумента к бесконечности. 20

Основные теоремы о пределах. 20

Бесконечно малые функции. 20

Бесконечно большие функции и их связь с бесконечно малыми. 21

Некоторые замечательные пределы. 21

Вычисление пределов. 22

Непрерывность функции в точке. 24

Точки разрыва и их классификация. 24

Непрерывность функции на интервале и на отрезке. 25

Дифференциальное исчисление функции одной переменной 26

Производная функции, ее геометрический и физический смысл. 26

Основные правила дифференцирования. 27

Производные основных элементарных функций. 27

Производная сложной функции. 28

Производная обратных функций. 28

Производная от функции, заданной параметрически. 28

Формула Тейлора. 29

Формула Маклорена. 30

Представление некоторых элементарных функций по формуле Маклорена. 30

Правило Лопиталя. 31

Производные и дифференциалы высших порядков. 32

Возрастание и убывание функций. 33

Точки экстремума. 33

Исследование функции на экстремум с помощью производных высших порядков. 33

Выпуклость и вогнутость кривой. Точки перегиба. 33

Асимптоты. 34

Схема исследования функций 36

Линейная алгебра.

Матрица размера mn.

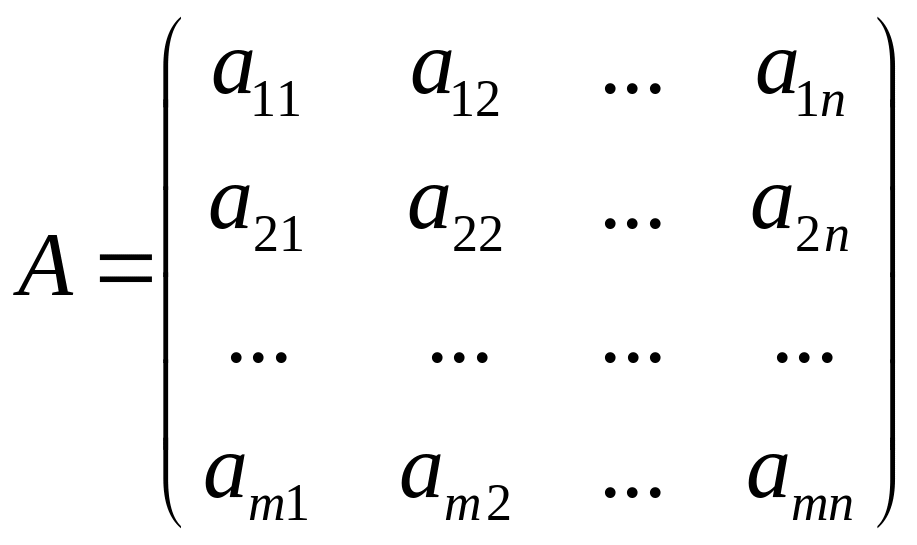
Основные действия над матрицами.

Если число столбцов матрицы равно числу строк ( ), то матрица называется квадратной.

Единичная матрица:

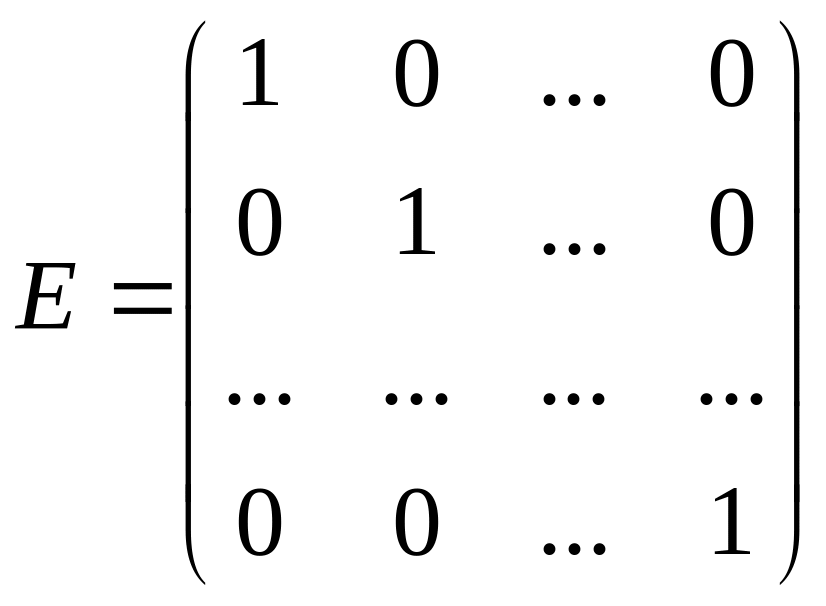
Диагональная матрица:

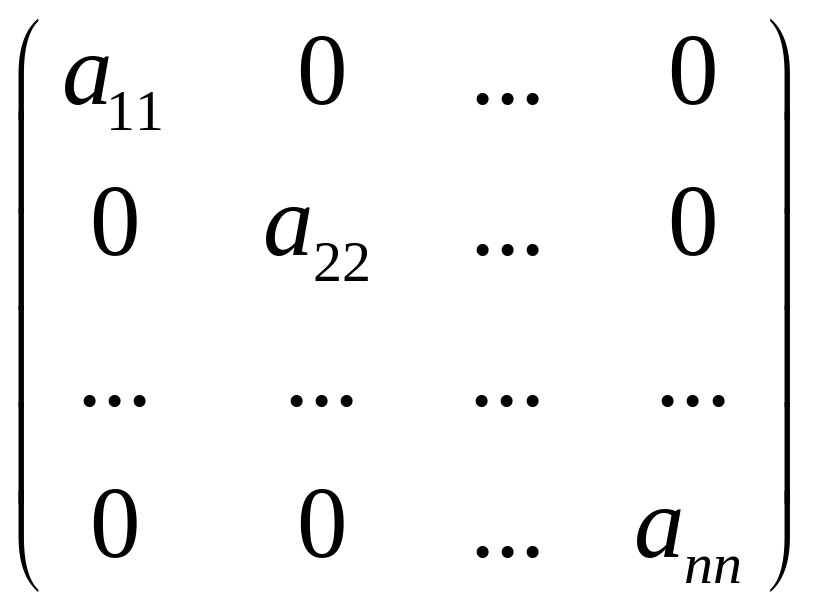
Если , то матрица называется симметрической.

Суммой (разностью) матриц является матрица, элементами которой являются сумма (разность) соответствующих элементов исходных матриц:

.

.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

Пример. Даны матрицы А и B, найти 2А + В.

,

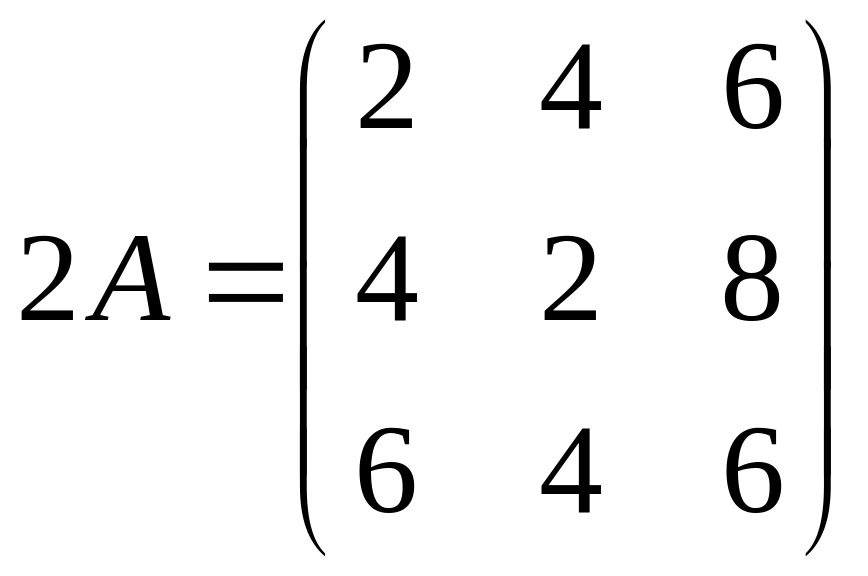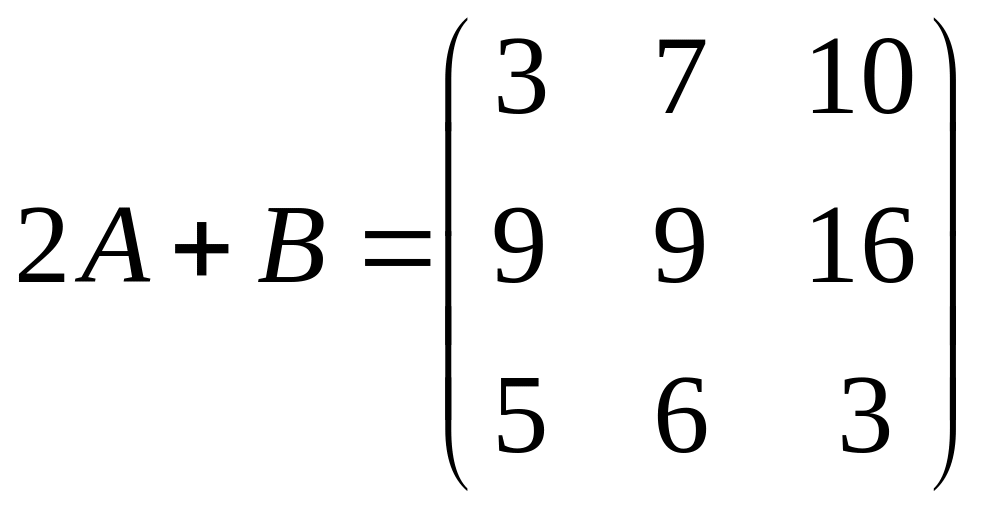
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

,

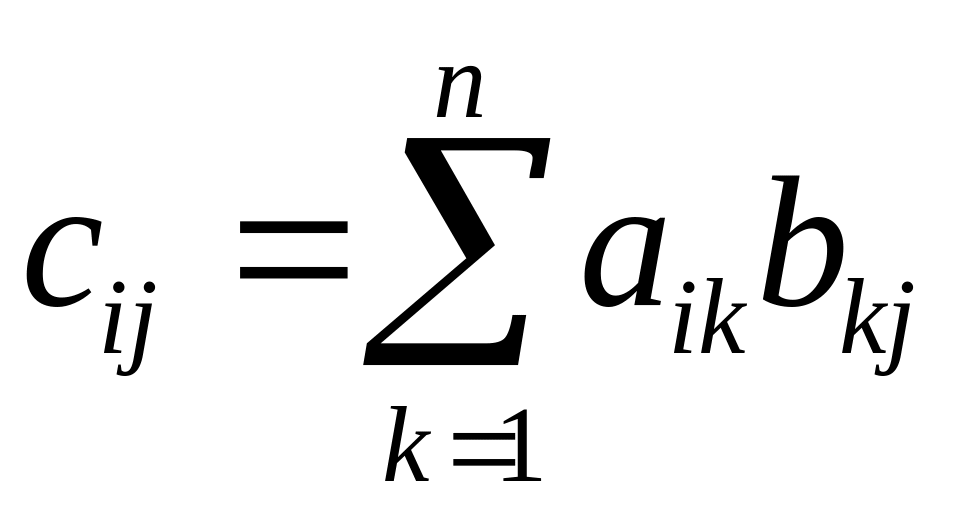
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Пример. Найти произведение матриц , .

.

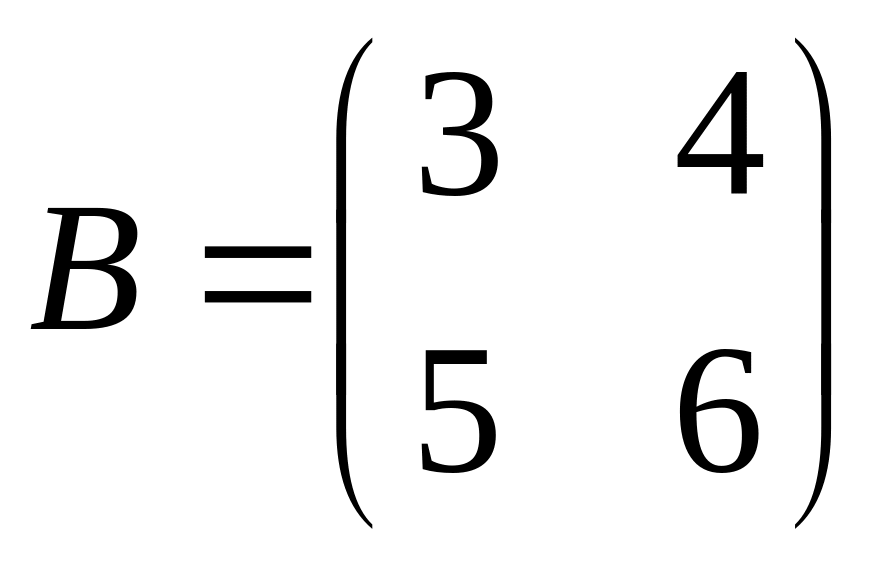Матрицу называют транспонированной матрицей , если элементы каждой строки матрицы записать в том же порядке в столбцы матрицы .

; ;

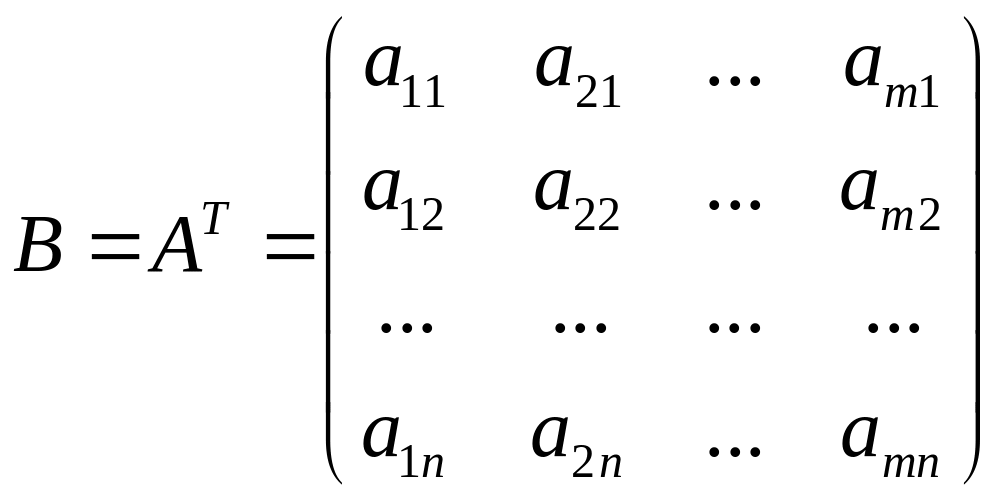другими словами, .

Определители.

Для матрицы первого порядка определителем является сам единственный элемент этой матрицы:

Для матрицы 2х2 определитель определяется как

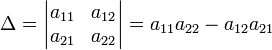
Для матрицы nxn определитель задаётся формулой:

,

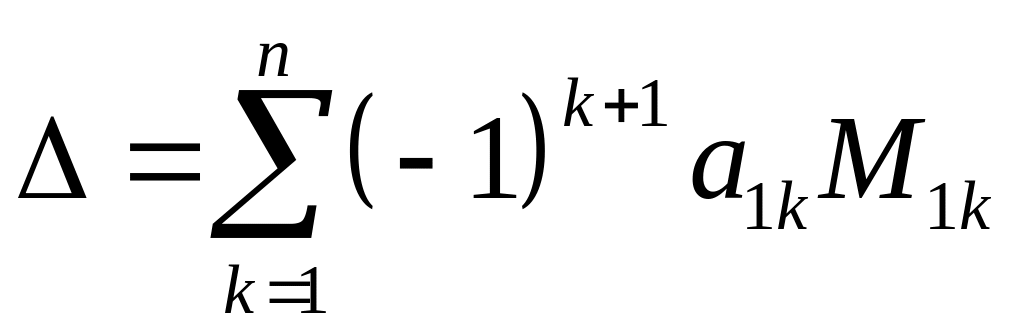где – минор к элементу . Он получается из исходной матрицы вычеркиванием первой строки и -го столбца.

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

,

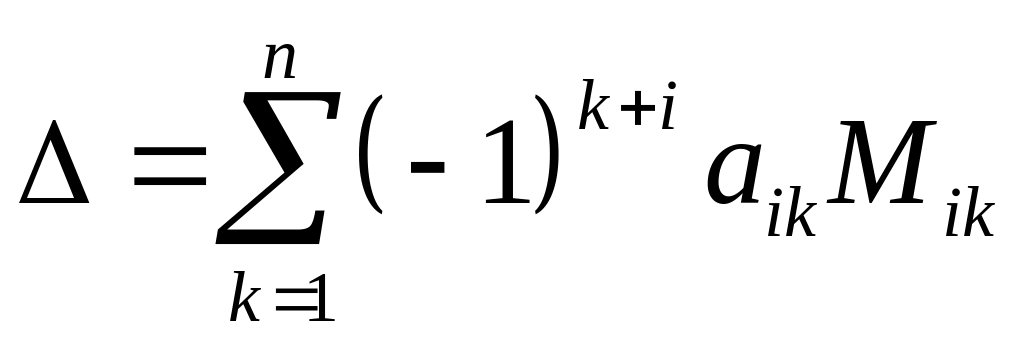Пример. Вычислить определитель матрицы .

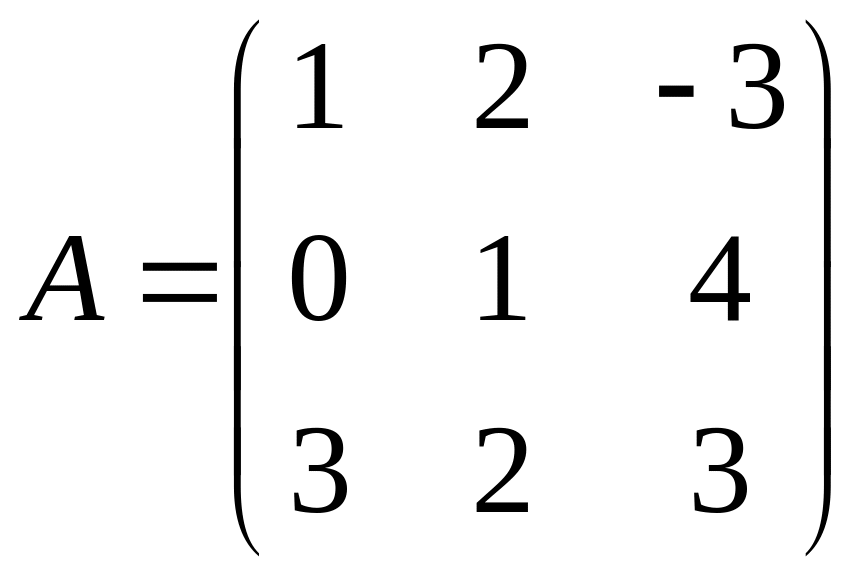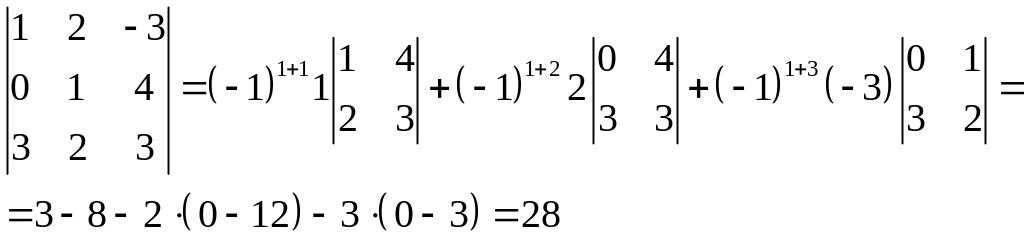
Или если вычислять по второй строке:

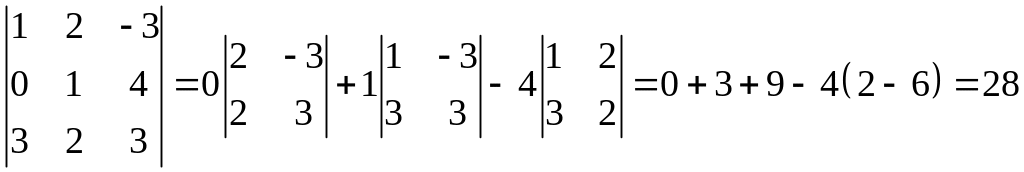
Матричный метод решения систем линейных уравнений.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Пусть дана система уравнений:

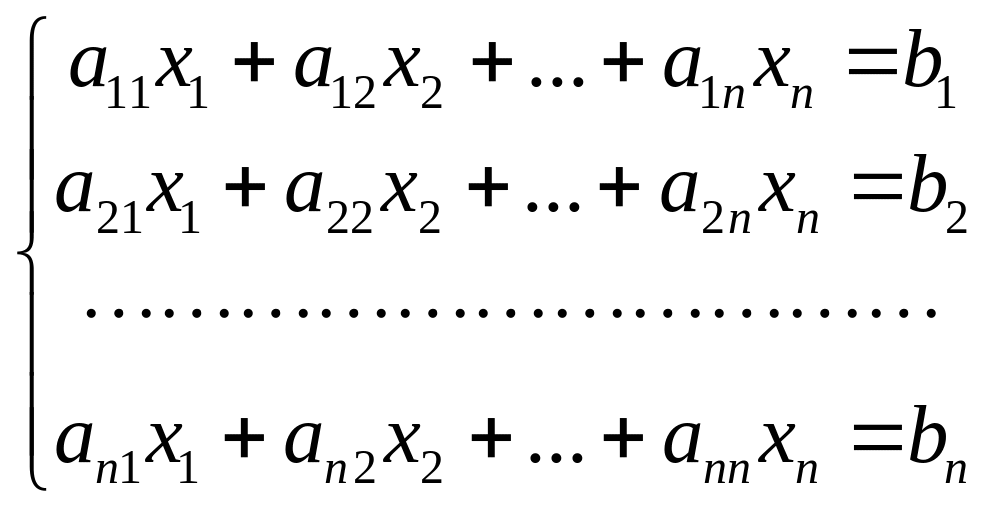
Составим матрицы: ; ; .

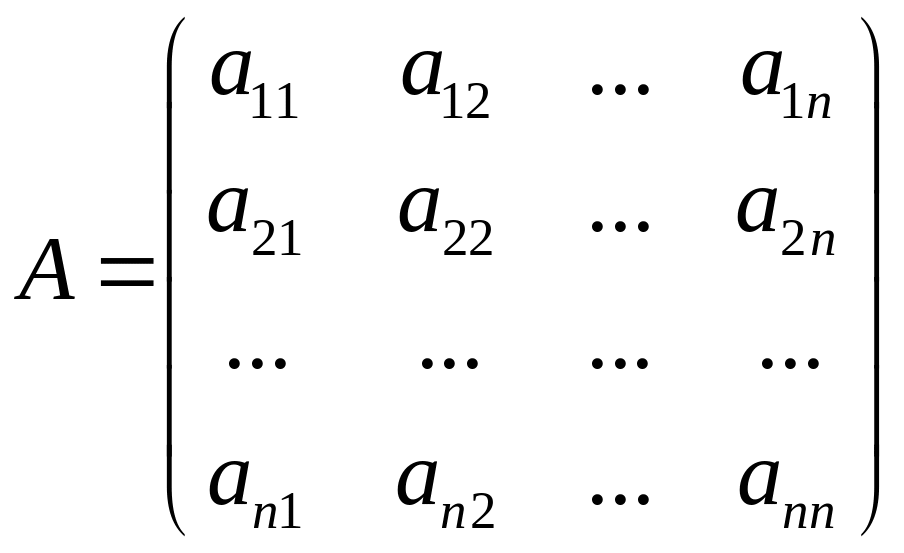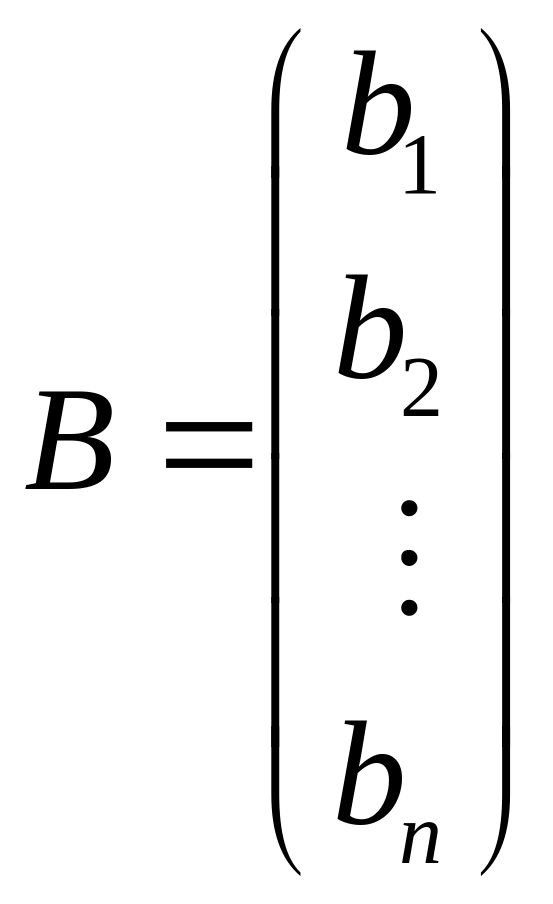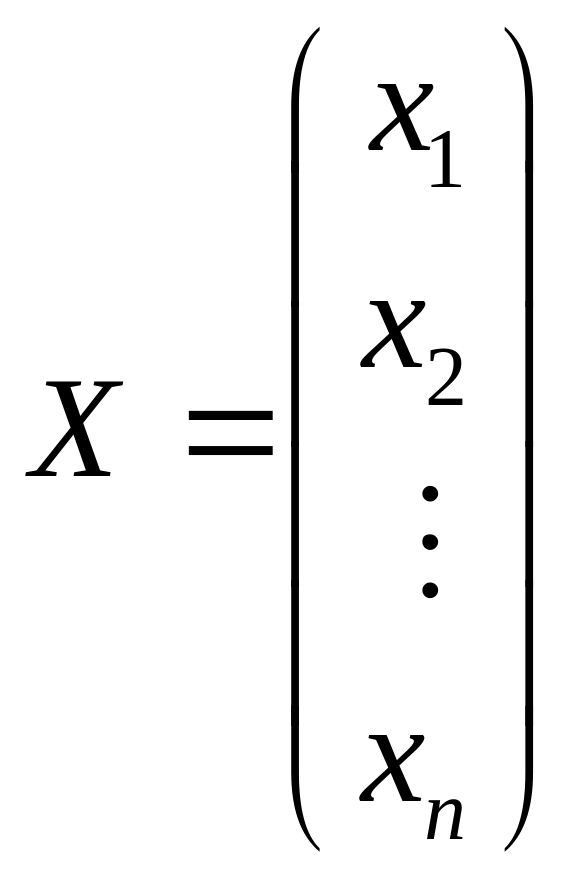Систему уравнений можно записать:

Для применения данного метода необходимо находить обратную матрицу.

Пример. Решить систему уравнений:

, ,

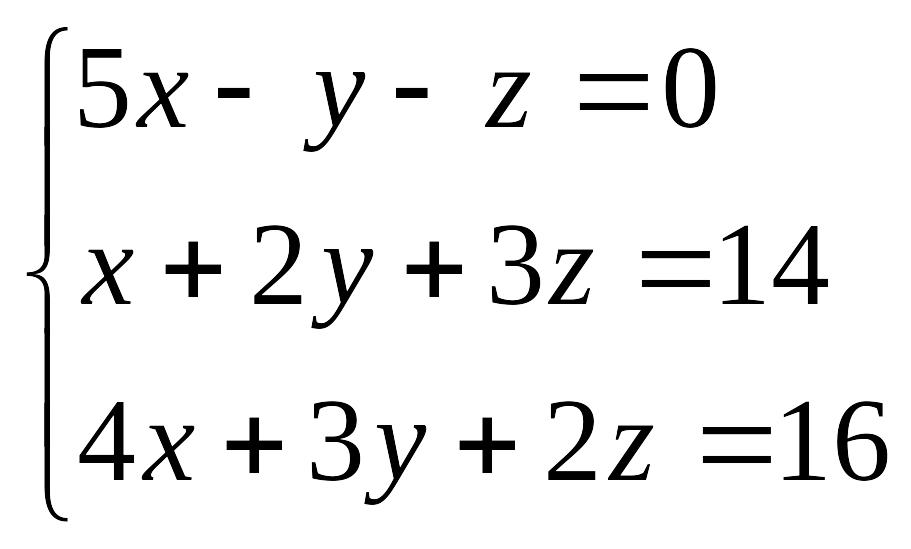
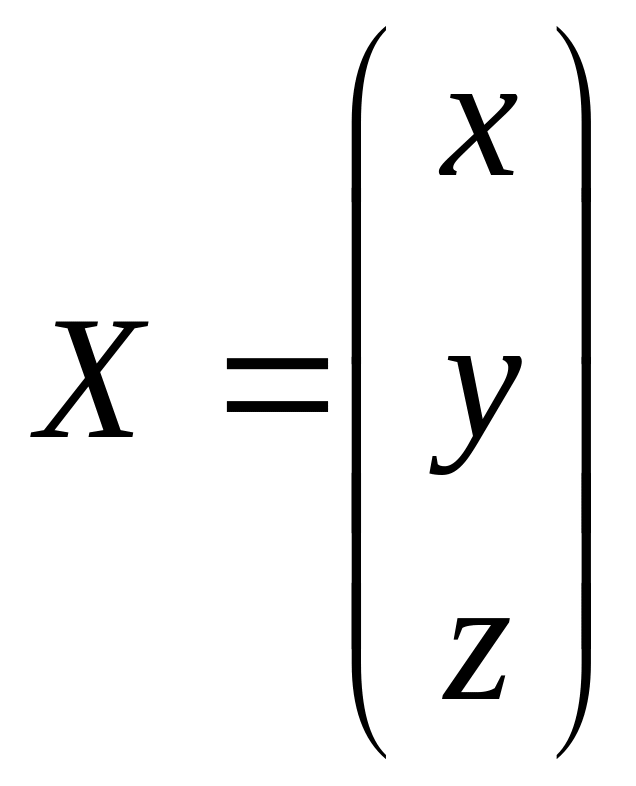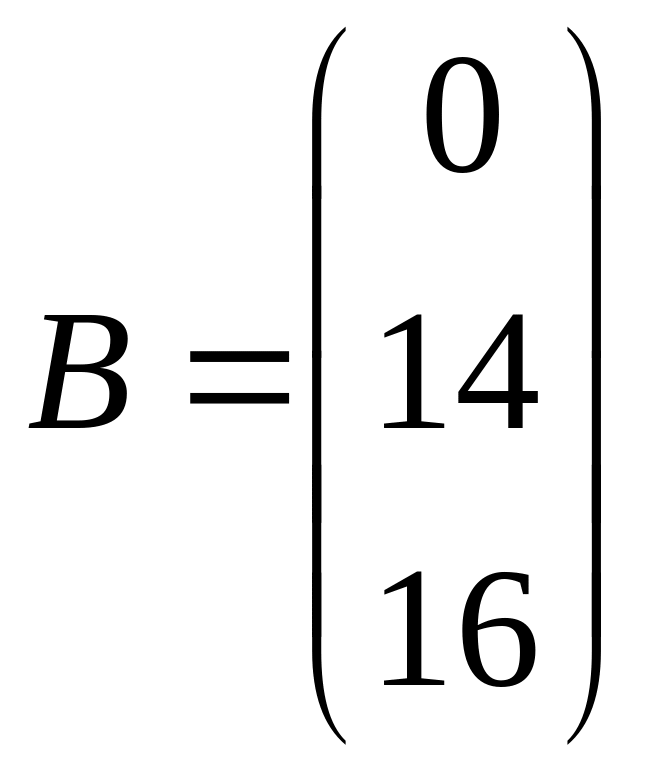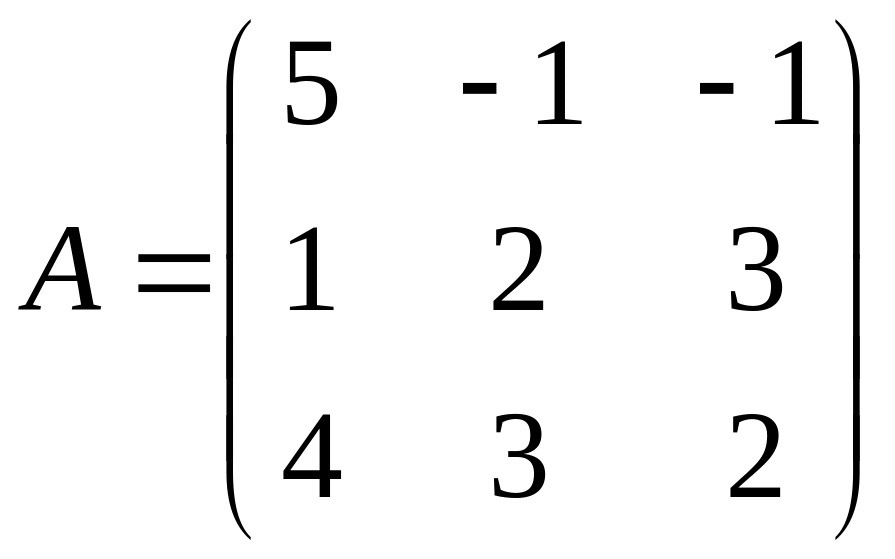
Найдем обратную матрицу.

.

Миноры:

; ; ;

; ; ;

; ; ;

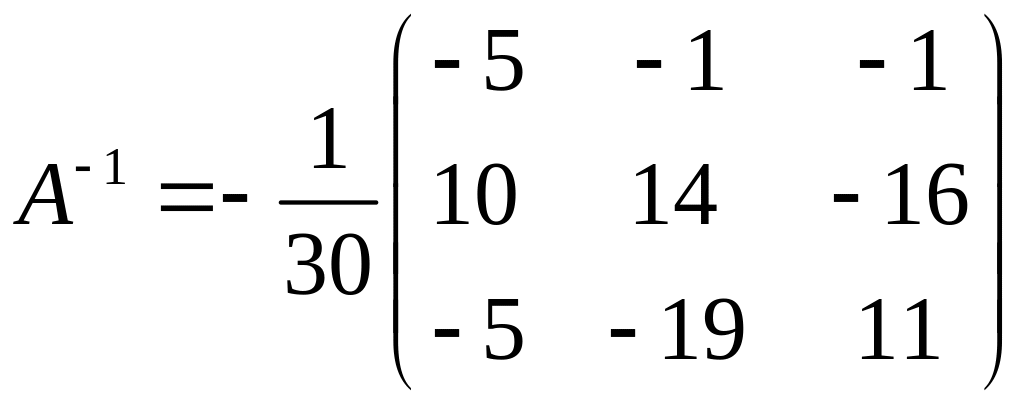
Находим матрицу Х.

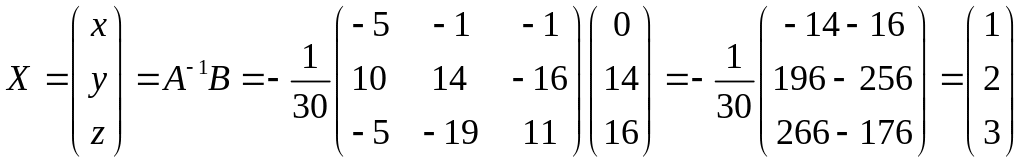
Итого решения системы: x =1; y = 2; z = 3.

Метод Крамера.

Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

,

где  = det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.

Пример. Найти решение системы уравнений:

.

.

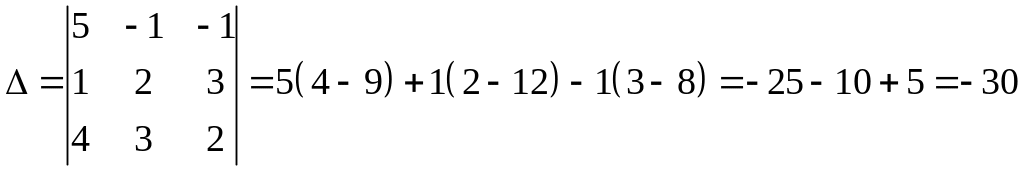
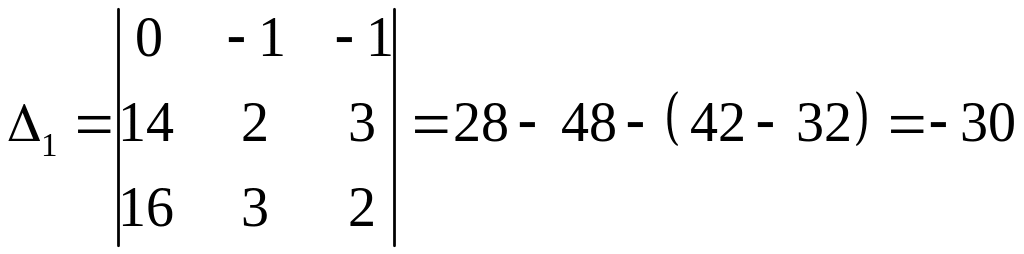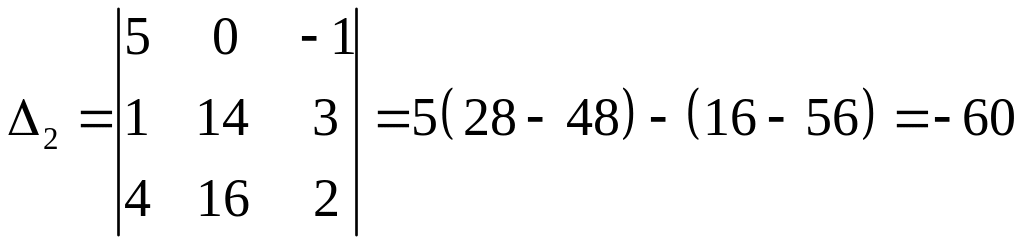
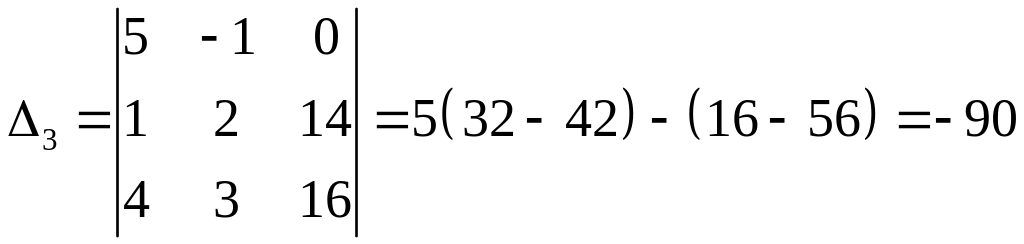
Элементарные преобразования систем.

1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2. Перестановка уравнений местами.

3. Удаление из системы уравнений, являющихся тождествами для всех х.

Метод Гаусса.

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

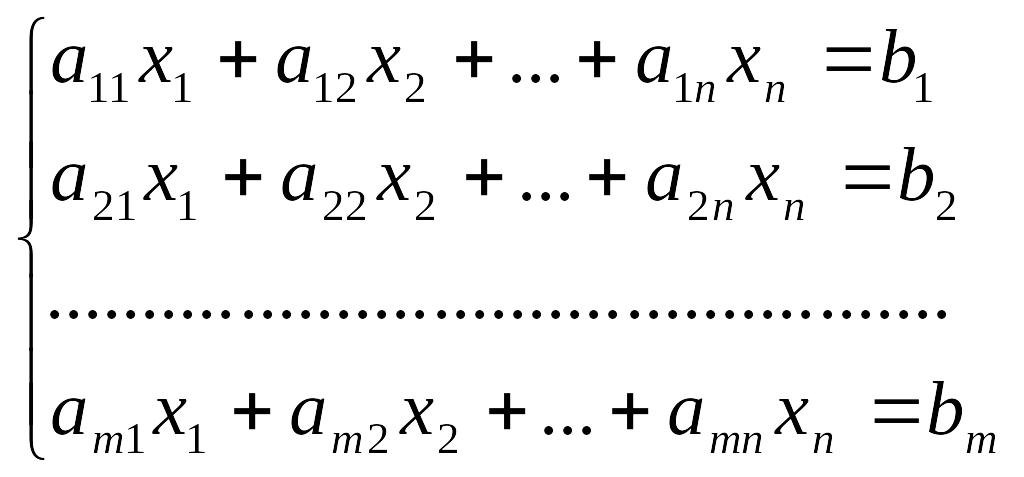
Разделим обе части 1–го уравнения на a11  0, затем:

1) умножим на а21 и вычтем из второго уравнения

2) умножим на а31 и вычтем из третьего уравнения

и т.д.

Получим:

,

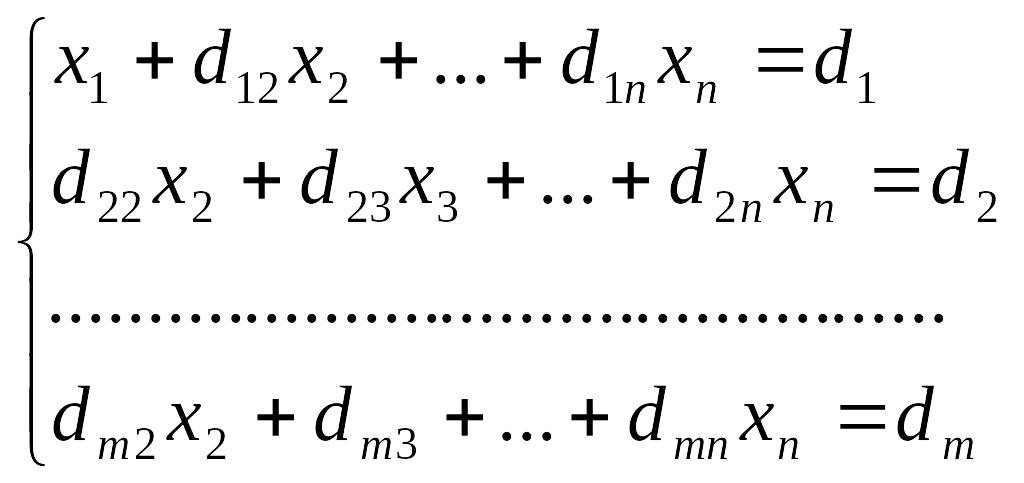где , , где i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения, потом для третьего и т.д.

Пример. Решить систему линейных уравнений методом Гаусса.

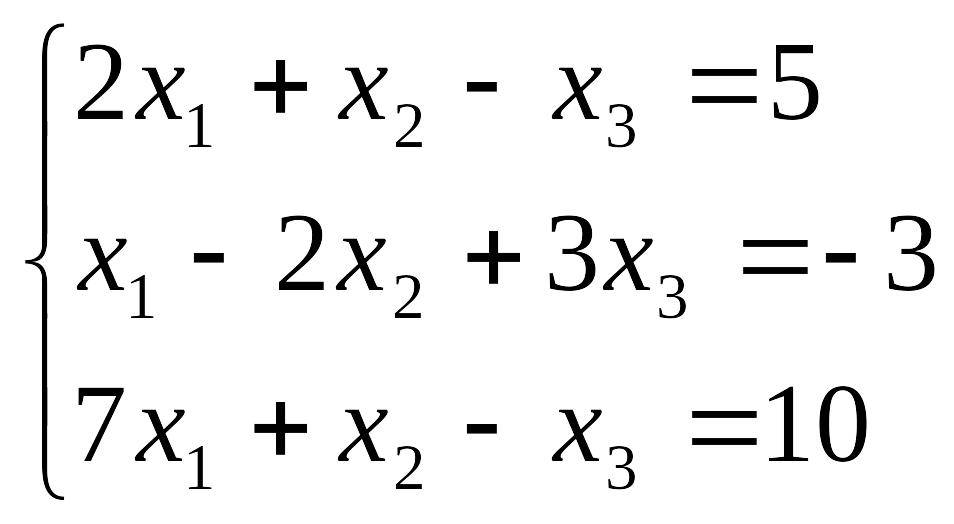
Составим расширенную матрицу системы.

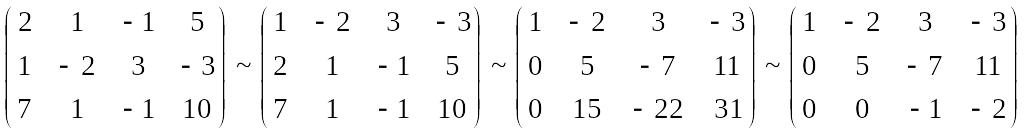
Таким образом, исходная система может быть представлена в виде:

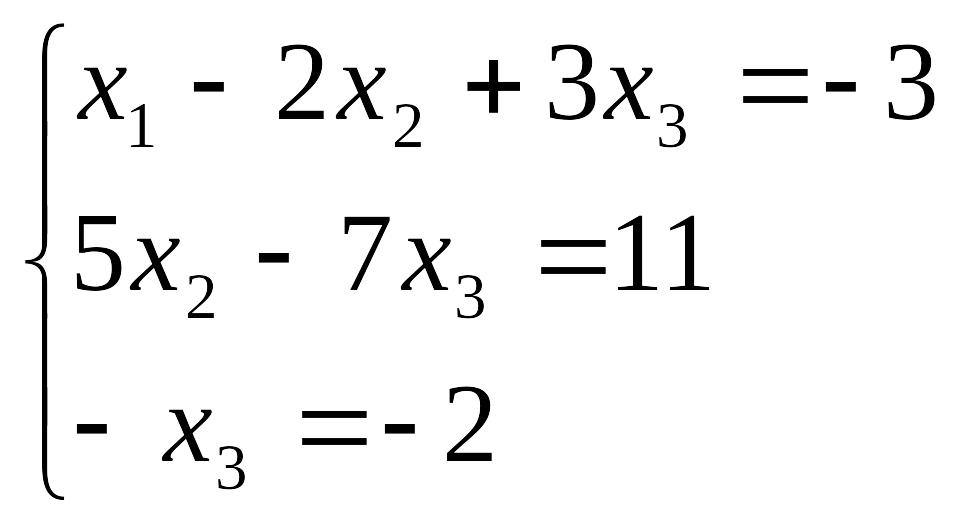, откуда получаем: x3 = 2; x2 = 5; x1 = 1.