Глава 13 ///////////////////////////////////////////////////////////////////////////////////

Плоскопараллельное движение тела

Скорость _B точки В плоской фигуры, полученной при сечении движущегося тела плоскостью, параллельной направляющей плоскости, равна геометрической сумме скорости _A полюса А фигуры и скорости данной точки В при вращательном движении фигуры вокруг оси, про­ходящей через полюс А и перпендикулярной плоскости фигуры:

_B = _A + ; AB; _BA= l_AB, (13.1)

где - угловая скорость фигуры, не зависящая от выбора полюса. Полюсом фигуры может служить любая ее точка.

Проекции скоростей двух точек твердого тела на пря­мую, соединяющую эти точки, равны между собой (теоре­ма о проекциях скоростей).

Мгновенный центр скоростей (МЦС) плоской фигуры – такая ее точка, скорость которой в данный момент времени равна нулю.

Скорости всех остальных точек плоской фигуры могут быть определены как скорости точек при вращательном движении фигуры вокруг МЦС:

_A l_AP ; AP , где точка Р - МЦС.

Ускорение точки В плоской фигуры равно геомет­рической сумме ускорения полюса А и ускорения данной точки В при вращательном движении фигуры

вокруг оси, проходящей через полюс А и перпендикуляр­ной плоскости фигуры:

(13.2)

= , , = ,

где - угловое ускорение фигуры, = d / dt = .

13.1. Механизм подачи бурового станка (рис. 13.1, а) приво­дится в движение с помощью цепи 7, огибающей звездочки 2, 2' и 3; последняя жестко связана с колесом 4, катящимся по рейке 5. Известны скорость цепи u, радиус R звездочки 3 и радиус r ко­леса 4. Определить скорость бурового инструмента и угловую скорость звездочки 3.

Рис. 13.1

Решение. Известно, что угловая скорость ведомой звез­дочки цепной передачи - величина переменная даже при посто­янной скорости цепи. Однако соблюдение определенных реко­мендаций при выборе конструктивных параметров передачи (числа зубьев звездочки, шага цепи и др.) позволяет снизить пе­риодическое изменение угловой скорости до 1 - 2 % [3]. В дан­ном случае, когда скорость цепи весьма мала, колебаниями угло­вой скорости звездочки 3 и колеса 4, а следовательно, и колеба­ниями скорости v перемещения бурового инструмента безусловно

можно пренебречь и считать, что скорость точки А звездоч­ки (рис. 13.1, б) равна скорости и цепи.

Полюс зацепления колеса 4 с неподвижной рейкой 5 является мгновенным центром скоростей (МЦС) звена 3-4 и по­этому угловая скорость звездочки

а скорость центра колеса, т. е. скорость перемещения бурового инструмента:

= r = r и /(R + r).

Ответ: = r и /(R + r); = .

13.2. Определить скорость v подъема бурового инструмента 1 и угловую скорость блока 2 (рис. 13.2, а), если скорость ка­ната 3 равна и, а радиус блока r.

Рис. 13.2

Решение. Канат, принимаемый за нерастяжимую нить, огибает блок 4, вращающийся вокруг неподвижной оси, следова­тельно, все точки каната на участке O₂C имеют в данный момент скорость , направленную вертикально вверх, а на участке ВА -такую же по величине скорость , но направленную вертикально вниз, т. е. _A =- и _A = = . МЦС блока 2 расположен в точке пересечения прямой AD и линии, проведенной через

концы векторов _A и (рис. 13.2, б). Поскольку скорости точек А и 02 одинаковы, то и отрезки АР₂ и Р₂0₂ равны между собой, т. е.

AP₂ = P₂O₂= r/2.

Скорость _D каната в точке D равна и, поэтому угловая скорость блока 2

= u / DP₂ = и / (r + r /2) = 2 и / (3r).

Скорость центра O₂ блока 2, т. е. скорость подъема бурового инструмента:

Ответ: = u / 3; = 2u / (3r).

13.3. Механизм подачи шпинделя 1 бурового станка при­водится в движение от гидроцилиндра 2 через систему блоков 3, ..., 6 (рис. 13.3, а). Скорость штока гидроцилиндра равна u, радиусы блоков одинаковы. Определить скорость шпинделя и отношение угловых скоростей блоков.

а б г

Рис. 13.3

Решение. Канат считаем гибкой нерастяжимой нитью. Крайняя левая ветвь каната неподвижна, скорости всех ее точек в длимый момент равны нулю, следовательно, точка А – МЦС блока 3 (рис. 13.3, б). Скорость центра этого блока равна скорости штока гидроцилиндра, тогда

;

Скорость точки С каната (рис. 13.3, в) по величине и на­правлению равна скорости точки В. Центр блока 4 неподвижен, поэтому

_A =- ; = = = 2u; ₄ = / r = 2 u / r.

Скорость точки Е каната по величине и направлению равна скорости точки D. Центр блока 5 движется со скоростью штока гидроцилиндра, поэтому картина скоростей точек этого блока, расположенных на горизонтальном диаметре, имеет вид, показанный на рис. 13.3, г, где точка Р₅ - МЦС блока 5. Угловая скорость блока 5

₅ = / (r-x) = / x, или и / (r-x) = 2 u/x,

откуда х = 2 r / 3, следовательно,

₅ = / (2r / 3) = ; = ₅

От точки F до места крепления со шпинделем все точки центральной оси каната имеют одинаковую по модулю скорость, вследствие этого скорость шпинделя = = 4u, а угловая ско­рость блока 6:

₆ = = 4 u / r.

Отношение угловых скоростей:

₃: ₄: ₅: ₆ =(u / r) :(2 u / r) :(3 u / r) : (4 u / r) = 1 : 2 : 3 : 4.

Ответ: ; ₃: ₄: ₅: ₆= 1 : 2 : 3 : 4.

13.4. Поворотная платформа экскаватора опирается на гусе­ницы в трех точках, являющихся вершинами равнобедренного треугольника ABC, в котором АС = ВС (рис. 13.4, а). Скорость точки А перпендикулярна АВ, скорость точки С направлена вдоль АС. Определить угловую скорость платформы и скорость точки В, если известны скорость точки А, длина стороны АВ треугольника (АВ = l) и угол α.

б

a

Рис. 13.4

Решение. Мгновенный центр скоростей платформы нахо­дится в точке пересечения перпендикуляров, восставленных из точек А и В к векторам скоростей этих точек (рис. 13.4, б).

Угловая скорость платформы

= _A /АР.

Вычисляем длину отрезка АР (см. рис. 13.4, б):

AP=AC/ cos α =

Тогда

Если > / 4, то _B > 0 и _{B A}; если < / 4, то _B < 0 и _{B A}; если = / 4, то _B = 0, т. е. вращение происходит вокруг вертикальной оси, перпендикулярной платформе и проходящей через точку В (МЦС - в точке В).

Ответ: = ; _B = _A |cos 2 |, причем _{B A}, если > / 4; _{B A}, если < / 4.

13.5. Внутри ходового колеса 1 (рис. 13.5, а) погрузочной машины помещен планетарный механизм, зубчатое колесо 2 ко­торого жестко связано с корпусом машины, движущейся посту­пательно. Колесо 3 вращается с известной угловой скоростью ю; оси колес 4 жестко связаны с ходовым колесом. Известно отно­шение чисел зубьев z₃ / z₄ = i и радиус R. Определить скорость корпуса машины, если проскальзывание ходовых колес по почве отсутствует.

б

a

Рис. 13.5

Решение. Колесо совершает плоскопараллельное движе­ние, которое можно представить состоящим из поступательного движения со скоростью центра солнечного колеса 3, т. е. со ско­ростью v корпуса машины, и вращательного движения вокруг этого центра с угловой скоростью .

Поскольку кинематические характеристики вращательной части движения не зависят от выбора полюса, такая разбивка движения на его составные части позволяет найти абсолютную угловую скорость колеса 1, рассматривая только его вращение вокруг неподвижной центральной оси.

Окружная скорость солнечного колеса 3

Сателлит 4 перекатывается по неподвижному коронному колесу 2, следовательно, МЦС сателлита совпадает с полюсом , 4 зацепления зубчатых колес 2 и 4 (рис. 13.5, б), при этом скорость центра O₄ сателлита 4 равна половине окружной скорости солнечного колеса ( = / 2).

Окружная скорость водила O₄O₃ равна скорости центра са­теллита 4, а отношение чисел зубьев колес равно отношению их радиусов, поэтому угловая скорость водила

Роль водила в заданном механизме выполняет ходовое коле­со 1, следовательно, = . Мгновенным центром колеса 1 является точка Р₁ (рис. 13.5, в) его контакта с почвой, поэтому скорость центра O₁ колеса 1, равная скорости корпуса машины, определяется как скорость точки тела при его вращении вокруг МЦС:

= O₁P₁ = = iR / [2(1 + i)].

Ответ: = iR / [2(1 + i)].

13.6. Планетарный исполнительный орган щита для проход­ки стволов (рис. 13.6, а) имеет режущие коронки 1, жестко свя­занные с зубчатыми колесами (сателлитами) 2, оси которых за­креплены на водиле 4 радиусом R. Колеса 2 перекатываются по неподвижному коронному колесу 3. Известны: отношение λ = R / r = 1,11; радиус коронки r = 0,72 м; отношение чисел зубьев i = z₃ / z₂ = 4,7; угловая скорость водила = 0,7 с^-1. Найти ско­рость режущего инструмента M, закрепленного на периферии коронки, положение которого определяется в данный момент уг­лом φ. Чему равны максимальная и минимальная скорости реза­ния?

б

a

Решение. Звено, состоящее из жестко связанных между собой режущей коронки 1 и зубчатого колеса 2 (сателлита), со­вершает плоскопараллельное движение. Чтобы найти скорость расположенного на коронке режущего инструмента М, достаточ­но знать его расстояние Р₂,₃М от мгновенного центра скоростей коронки и ее угловую скорость.

МЦС коронки совпадает с полюсом Р_2,3 зацепления сател­лита с неподвижным коронным колесом 3 (рис. 13.6, б).

Скорость центра O₁ сателлита равна окружной скорости во­дила OO₁.

Угловую скорость сателлита определяем, учитывая, что от­ношение радиусов начальных окружностей находящихся в зацеп­лении зубчатых колес равно отношению чисел их зубьев:

Расстояние Р_2,3 М находим по теореме косинусов:

Р_2,3 М = ,

где - радиус коронки ( = r); - радиус начальной окружно­сти сателлита ( = - R). Поскольку = i, а R = λ, то = r₂i - λ, откуда - λ /(i - 1). Следовательно,

Р_2,3 М = =

.

Теперь можно вычислить скорость режущего инструмента:

= .

Скорость резания минимальна, когда = 1, а = 0:

=1,305 м/с.

Скорость резания максимальна, когда = -1, а = π:

=2,424 м/с.

Ответ:

; ;

13.7. Поршень A механизма поворота ковша автопогрузчика (рис. 13.7, а) движется равномерно со скоростью _A = 0,1м/с. Для положения, изображенного на рисунке, определить скорости точек С, D и Е, а также угловые скорости всех ведомых звеньев механизма, если .

Рис. 13.7

Решение. Точка В принадлежит одновременно поршню А и шатуну ВС. Поршень перемещается в прямолинейных неподвиж-ных направляющих, следовательно, его движение - посту­пательное, скорости всех его точек одинаковы, т.е. _B = _A = 0,1 м/с.

Траекторией точки С является дуга окружности радиусом ОС, поэтому ОС. Проведя перпендикуляр к вектору до пересечения с перпендикуляром к , находим МЦС шатуна ВС, в данном случае совпадающий с точкой О. Поскольку Δ ОВС -равносторонний, то СО = ВО, поэтому v_C = v_B = 0,1 м/с.

Скорости точек плоской фигуры пропорциональны их рас­стояниям от МЦС, поэтому

v_D = 2 v_C = 0,2 м/с.

Вектор скорости точки Е, как и вектор скорости точ­ки D, направлен по прямой DE, поэтому в соответствии с теоре­мой о проекциях скоростей (см. начало главы)

v_E = v_D = 0,2 м/с.

Отметим, что МЦС шатуна DE находится в бесконечности (так как перпендикуляры к векторам и параллельны), следовательно, движение этого звена в данный момент мгновен­но поступательное и ω_DΕ=0.

Находим угловые скорости остальных звеньев:

Ответ: v_C = 0,1 м/с; v_D = 0,2 м/с; ν_E = 0,2 м/с;

13.8. Кривошип OA механизма грохота (рис. 13.8, а) вра­щается с частотой n = 1000 мин^-1. Для положения, показанного на рисунке, определить скорости точек В, D и Е, а также угловые скорости всех ведомых звеньев механизма, если l_OA = 0,2 м, l_AB = 0,45 м, l_BC = 0,5 м, l_CD = 0,7 м, l_DE = 0,8 м.

Решение. Скорость пальца А кривошипа

= 20,944 м/с.

Рис. 13.8

б

а

МЦС шатуна ΑΒ (точка P_AB, рис. 13.8, б) находится на пере­сечении перпендикуляров к векторам скоростей точек А и B по­этому угловая скорость шатуна

Тогда скорость точки В

v_B = = 0,5 = 0,5 ν_A = 10,472 м/с.

Теперь можно найти угловую скорость коромысла CD и ско­рость точки D:

= v_B / = 10,472 / 0,5 = 20,944 с"¹;

v_D = = 20,944 0,7 = 14,661 м/с.

МЦС шатуна DE (точка P_DE, рис. 13.8, б) находится на пе­ресечении перпендикуляров к векторам скоростей точек D и Е, т. е. на пересечении продолжения отрезка DC и перпендикуляра к направляющей ползуна Е. Полученный треугольник DEP_DE -равнобедренный, P_DEE = DE.

По теореме о проекциях скоростей имеем

v_E cos 30° = v_D cos 60°,

откуда v_E = v_D tg 30° = 14,661 tg 30° = 8,464 м/с.

Угловая скорость шатуна DE

= v_E /P_DEE = v_E / = 8,464 / 0,8 = 10,58 c ^-1.

Угловая скорость ползуна Ε равна нулю.

Ответ: ν_Β 10,47 м/с; v_D 14,66 м/с; v_E 8,46 м/с;

40,31 с ^-1; 20,94 с ^-1; = 10,58 с ^-1.

13.9. Кривошип OA механизма шоковой дробилки вращается с частотой n = 300 мин ^-1 (рис. 13.9, а). Для положения, изобра­женного на рисунке, определить скорости точек В и D, а также угловые скорости всех ведомых звеньев механизма, если l_OA =

= 0,12 м, l_AB = 0,25 м, l_BC = 0,3м, l_BD = 0,35 м, l_DE = 0,8м.

Рис. 13.9

б

a

Решение. Скорость пальца А кривошипа

= 3,77 м/с.

Траектория точки А - окружность радиусом OA, траектории точек В и D - дуги окружностей, радиусы которых соответ­ственно СВ и ED (рис. 13.9, б). Векторы скоростей этих точек, касательные к соответствующим траекториям, показаны на ри­сунке. Восставив перпендикуляры из рассматриваемых точек к векторам их скоростей, находим МЦС шатунов АВ и BD (соот­ветственно точки Р_AB и P_BD на рис. 13.9, б).

Для определения скоростей v_B и v_D применим теорему о проекциях скоростей:

v_A cos 60° = v_B cos 30° и v_D cos 0° = v_B cos 30°,

откуда

v_B= v_A tg 30° = 3,77 tg 30° = 2,177 м/с;

v_D = v_A cos 60° = 3,77 cos 60° = 1,885 м/с.

Угловые скорости ведомых звеньев находим с помощью МЦС, предварительно из равнобедренного треугольника АВР_AB и прямоугольного треугольника BDP_BD определив полюсные рас­стояния:

Р_ABВ = и P_BDВ = 2 l_BD .

Тогда

Ответ: v_B 2,18 м/с; v_D = 1,885 м/с; 8,71 ;

7,26 ; 3,11 с"¹; 3,14 с^-1.

13.10. Кривошип OA механизма грохота (рис. 13.10, а) вра­щается с частотой n = 1500 мин . Для положения, показанного на рисунке, определить скорости точек В, D и Е, а также угловые скорости всех ведомых звеньев механизма, если = 0,15 м, = =0,08 м, l_BD = 0,36 м, = 0,25 м.

а

б

Рис. 13.10

Решение. Скорость пальца А кривошипа

= 23,562 м/с.

Траектория точки А - окружность радиусом OA, траектории точек В и D - дуги окружностей, радиусы которых соответ­ственно СВ и СД траектория точки С - отрезок горизонтальной прямой линии. Векторы скоростей этих точек, касательные к со­ответствующим траекториям, показаны на рис. 13.10, б. Восста­вив перпендикуляры из рассматриваемых точек к векторам их скоростей, находим МЦС шатуна DE (точка Р_DE) и убеждаемся, что МЦС шатуна АВ находится в бесконечности, т.е. этот шатун в данный момент движется мгновенно поступательно, его угловая скорость = 0, а скорости точек А и В одинаковы.

Поскольку при вращательном движении тела скорости его точек прямо пропорциональны радиусам их траекторий, скорость vd точки D коромысла CD

Для определения скорости v_E точки Ε шатуна DE применим теорему о проекциях скоростей:

v_E cos 15^o = v_D cos30^o,

откуда

ν_E = v_D cos 30° / cos 15° = 129,591 cos 30° / cos 15° = 116,188 м/с.

Угловая скорость коромысла CD, совершающего вращатель­ное движение,

= v_B / l_BC = 23,562 / 0,08 = 294,525 с^-1.

Угловую скорость шатуна DE находим с помощью МЦС, предварительно из треугольника DEP_DE определив по теореме синусов полюсное расстояние Р_DEЕ = l_DE sin 60° / sin 15°.

Тогда

= v_E /P_DEE = (ν_E sin 15°) / (l_DE sin 60°) =

= (116,188 sin 15°) / (0,25 sin 60°) = 138,895 с ^-1.

Угловая скорость ползуна Ε равна нулю.

Ответ: ν_Β = ν_Α 23,56 м/с; v_D 129,6 м/с; v_E 116,2 м/с;

= = 0; 294,5 с ^-1; 138,9 с ^-1.

13.13. При срабатывании предохранительной планетарной муфты (рис. 13.13, а) роторного экскаватора наружное (коронное) колесо 1 начинает вращаться из состояния покоя с постоянным угловым ускорением ε. Ведущее (солнечное) колесо 2 вращается равномерно с угловой скоростью ω. Известно отношение чисел зубьев колес 3 и 2: z₃ / z₂ = i. Определить угловое замедление водила OA и время движения колеса 1 до остановки водила.

a

б

в

г

Рис. 13.13

Решение. На рис. 13,13, б, в, г показаны картины распре­деления скоростей точек механизма, расположенных в верти­кальном радиальном его сечении, для момента начала движения наружного (коронного) колеса 1 (схема «б»), промежуточного положения (схема «в») и момента остановки водила (схема «г»). Из этих рисунков видно, что скорость центра А сателлита 3, рав­ная окружной скорости водила OA, равна половине геометри­ческой суммы скоростей крайних точек вертикального сечения сателлита:

где ν₂ - окружная скорость солнечного колеса 2 (ν₂ = ωr₂); r₂ - радиус его начальной окружности; ν₁ - окружная скорость корон­ного колеса 1 (ν₁ = ω₁ r₁; ω₁ - его угловая скорость; r₁ - радиус начальной окружности короны (r₁ = r₂ + 2 r₃); r₃ - радиус началь­ной окружности сателлита 3. Поскольку радиусы начальных окружностей зубчатых колес прямо пропорциональны числам зубьев, то r₃ / r₂ = z₃ / z₂ = i, откуда r₃ = r₂ i.

Угловая скорость водила

Дифференцируя по времени с учетом ω = const, имеем

Направление углового ускорения _OA водила совпадает с направлением углового ускорения ε коронного колеса, т. е. про­тивоположно направлению вращения водила. Следовательно, вращение водила является равнозамедленным и до полной его остановки происходит по закону

Начальное значение угловой скорости водила нахо­дим по формуле (1) при условии, что = 0:

= ω/[2(1 + i)].

Тогда

Моменту остановки водила соответствует = 0, т. е.

= 0, или t = ω/ [ε (1 + 2 i)].

Ответ: = ε (1 + 2 ί)/ [2 (1 + i)]; t = ω/ [ε (1 + 2 i)].

13.14. Система, состоящая из стержня АВ, шарнирно соеди­ненного с ползунами А и В (рис. 13.14, а), является моделью шахтной вагонетки: ползуны - передняя и задняя колесные пары, стержень - кузов вагонетки. Определить угловое ускорение кузо­ва, а также ускорение его центра тяжести С в тот момент време­ни, когда передняя колесная пара, двигаясь равномерно со скоро­стью ν, въезжает на закругление радиусом R. Известно расстоя­ние l_AB = l; l_FC = l_BC .

в

а

б

Рис. 13.14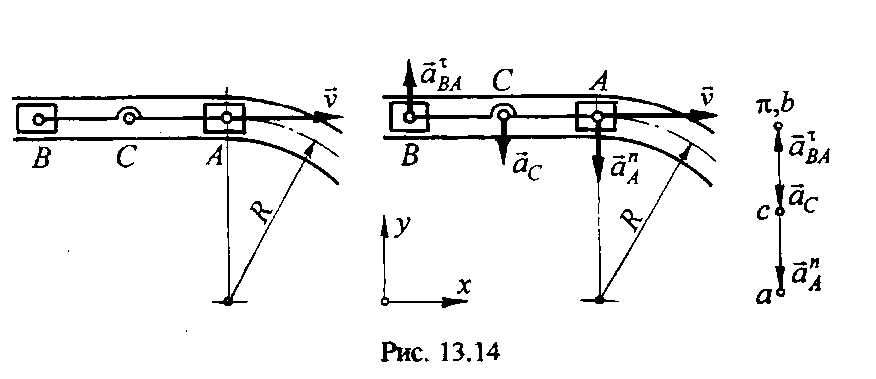

Решение. Векторы скоростей , и соответ­ственно точек А, В и С (рис. 13.14, б) в рассматриваемый момент времени расположены на прямой АВ (и ее продолжении), поэтому согласно теореме о проекциях скоростей

v_A = v_B = v_C = v.

Угловая скорость стержня = 0, так как МЦС находится в бесконечности (перпендикуляры к векторам скоростей парал­лельны друг другу).

Принимаем точку А за полюс, тогда ускорение точки В [см. уравнение (13.2) в начале данной главы

где а_B - ускорение точки В; поскольку движение этой точки прямолинейное и равномерное, то а_B = 0;

- нормальное ускорение точки A ( = ν² /R);

- тангенциальное ускорение точки А ( =dv/dt);

по условию задачи ν = const, следовательно, = 0;

нормальное ускорение точки В при вращении стерж­ня

АВ вокруг полюса Α ( = ); b рассмат­риваемый

момент времени = 0, поэтому =0;

тангенциальное ускорение точки В при вращательном

движении стержня вокруг полюса А ( = )

подлежащее определению угловое ускорение стержня.

После подстановки известных величин получаем

Проецируем полученное векторное уравнение на ось у:

откуда = .

Тогда .

Для определения ускорения точки С составляем вектор­ное уравнение, аналогичное векторному уравнению для опреде­ления ускорения :

Проецируем полученное векторное уравнение на оси x и у:

;

Но , следовательно,

и а_C = |a_Cy| = /2 = v²/(2R).

Ответ: = ; а_C = v²/(2R).

13.15. При разгрузке скип 1 карьерного канатного подъема роликом В опирается на разгрузочную кривую, имеющую форму

дуги окружности радиусом R = 1 м, и поворачивается относи­тельно рамы 2 вокруг шарнира А (рис. 13.15, а). Для положения, показанного на рисунке, определить угловую скорость и угловое ускорение скипа, если скорость рамы ν = 2 м/с; ее замедление

а = 0,8 м/с²; 2,2 м.

Рис. 13.15, а, б

б

a

Решение. Рама скипа движется поступательно, следова­тельно, скорость шарнира А, установленного на раме, = , его замедление ⁼ Скорость ролика В, принимаемого за точ­ку, направлена по касательной к траектории его движения, т. е. к разгрузочной кривой (рис. 13.15, б). Точка P₁ пересечения пер­пендикуляров, восставленных в точках А и В к векторам и , является мгновенным центром скоростей скипа. Полюсное расстояние P₁А находим из треугольника АВP₁ с помощью тео­ремы синусов:

P₁А = ( sin 105°)/sin 45°.

Угловая скорость скипа

ω = ν_Α / P₁А = (ν sin 45°) / ( sin 105°) =

= (2 sin 45°) / (2,2 sin 105°) = 0,666 c ^-1.

Скорость точки В определяем, используя теорему о проекции скоростей:

v_B cos 15° = ν_Α cos 60°,

откуда

Чтобы найти угловое ускорение скипа, надо вычислить тангенциальное ускорение из уравнения

+ = + + , (1)

полученного из уравнения (13.2) с учетом того, что точка B совершает криволинейное движение, поэтому ее полное ускорение состоит из нормального и тангенциального.

Нормальные ускорения:

м/с ;

= ∙ 2,2 = 0,976 м/ .

Рис. 13.15, в

Графическое решение уравнения (1), называемое планом ускорения, показано на рис. 13.15, в.

Чтобы определить аналитически, нужно спроецировать уравнение (1) на ось , перпендикулярную второму неизвестному, т.е. тангенциальному ускорению :

= cos sin + cos ,

откуда

= ( cos + sin ) / cos =

= (1,071 0,8 cos + 0,976 sin ) / cos = 0,785 м/ .

Угловое ускорение скипа

ε = / = 0,785 / 2,2 = 0,357

Ответ 𝜔 ≈ 0,67 ε ≈ 0,36 .

13.16. Для положения, показанного на рис. 13.16, а, определить угловую скорость и угловое ускорение скипа AB, а также ускорение B, если =1,2 м/ , =0,6 м/ , = 2,3 м, R= 3 м, радиус колеса r = 0,25 м.

а б

_A

R

Рис. 13.16, а,б

Решение. Предварительно уточним значение , которое соответствует заданным на рис. 13.16, а значениям углов. В че­тырехугольнике АВОС (рис. 13.16, б) угол ОСА - прямой, ОС = = ОВ - R + r. Треугольник ОВС - равносторонний. ACB = 30°. Из треугольника АСВ по теореме синусов получаем

= (R+r) = (3+0.25) = 2.298 м.

Отклонение от заданной величины не превышает 0,1 %, что вполне допустимо, но тем не менее в дальнейших расчетах мы будем использовать вновь найденное значение .

Скорость точки В определяем с помощью теоремы о проек­циях скоростей на прямую АВ:

v_B cos 15° = v_A cos 45°,

откуда

v_B = (v_A cos 45°) / cos 15° = (1,2 cos 45°) / cos 15° = 0,878 м/с.

МЦС рамы АВ скипа – это точка пересечения перпендикуляров, восставленных из точек А и В к векторам _A и _B (рис. И 16, б). Полюсное расстояние находим из треугольника по теореме синусов:

= sin 75°) / sin 60° = (2,298 sin 75°) / sin 60° = 2,563 м.

Угловая скорость скипа

𝜔 = v_A / = 1,2 / 2,563 = 0,468 .

Чтобы найти угловое ускорение скипа, надо вычислить тангенциальное ускорение из уравнения

+ = + + (1)

полученного из уравнения (13.2) с учетом того, что точка В со­вершает криволинейное движение, поэтому ее полное ускорение состоит из нормального и тангенциального. Нормальные ускорения:

= / (R + r) = 0,878² / (3 + 0,25) = 0,237 м/с²;

= = 0,468² ∙ 2,298 = 0,504 м/с².

Графическое решение урав­нения (1), называемое планом ускорений, показано на рис. 13.16, е.

Выбрав направления осей координат так, как указано на рис.13.16, в, проецируем уравнение (1) на эти оси:

Рис. 13.16, в

sin 15° + cos 15° = а_А sin 45° + ;

cos 15° - sin 15° = а_А cos 45° - ,

откуда

= (а_А sin 45° + - sin 15°) / cos 15° =

= (0,6sin 45° + 0,504 - 0,237sin 15°)/cosl5° = 0,897 м/с²;

= - cos l5° + sinl5^o + а_А cos45^o =

= - 0,237 cos 15° + 0,897sin 15° + 0,6 cos 45° = 0,427 м/с².

Полное ускорение точки В:

а_А = = д/о,237²+0,897² = 0,928 м/с².

Угловое ускорение скипа

ε = / = 0,427 / 2,298 = 0,186 .

Ответ: 𝜔 ≈ 0;47 с^-1; ε ≈ 0,19 ; а_B ≈ 0,93 м/с².

13.17. Механизм грохота состоит из кривошипа I, вращаю­щегося равномерно вокруг центра О с частотой = 120 , шатуна 2 и сита 3, подвешенного на параллельных стержнях 4 и 5, шарнирно прикрепленных к стойке 6 (рис. 13.17, а). Известно, что = 0,2 м, = 0,8 м, = = 0,5 м. Для заданного поло­жения механизма определить скорость и ускорение сита, а также угловые скорости и угловые ускорения звеньев 2 и 4.

Решение. При решении данной задачи используем метод планов скоростей и ускорений.

Рис. 13.17,6

Траектория пальца А кривошипа - окружность радиусом ОА ( рис 13. 17, б). Скорость пальца

v_A = = ( / 30) = ( ∙ 120 / 30) 0,2 = 2,513 м/с.

Траектории точек В и Е - одинаковые дуги окружностей (их радиусы и равны по условию задачи). Следовательно, _A OA; _B ВС; _E DE; _B || _E (так как стержни 4 и 5 па­раллельны).

Принимая за полюс точку А, записываем векторное уравне­ние скорости точки В:

_B = _{A BA} (1)

Скорость точки А известна по величине и направлению, из­вестны также линии действия векторов _B и _BA ( _BA AB, см. пояснения в начале главы). Таким образом, в уравнении (1) име­ются только две неизвестные величины модули скоростей _B и _BA

в

Рис. 13. 17, в, г

Для графического решения этого уравнения из произвольно выбранной точки p_v , называемой в дальнейшем полюсом плана скоростей, откладываем вектор , изображающий в некото­ром масштабе [(м/с)/мм] скорость точки А (рис. 13.17, в). Заме­тим, что ↑↑ _A и p_v a = v_A / . Поскольку в соответствии с уравнением (1) к вектору _A следует прибавить вектор _BA, то из конца вектора проводим луч, параллельный линии действия вектора _BA до пересечения с лучом , проведенным из полю­са p_v параллельно линии действия вектора _B. Полученная фи­гура (в данном случае - треугольник p_v ab) называется планом скоростей звена АВ. Совокупность планов скоростей всех звеньев механизма, построенная из одного полюса ,

носит название плана скоростей механизма. Отметим, что на плане скоростей векторы абсолютных скоростей точек имеют своим началом по­люс плана, а векторы относительных скоростей соединяют на плане концы векторов абсолютных скоростей соответствующих точек.

Из плана скоростей следует, что v_B = (p_vb) и v_BA = (ab). Принимая во внимание, что треугольник b - равносторон­ний, так как каждый его угол равен 60°, получаем

a= b= ab, или v_A = v_B = v_BA = 2,513 м/с.

Векторное уравнение скорости точки Е, отнесенной к ситу 3:

_E= _B + _EB. (2)

Для решения этого уравнения проводим из точки b плана скоростей луч, перпендикулярный BE, поскольку _EB BE, а из полюса р_у - луч, перпендикулярный DE (параллельный линии действия скорости _E). Эти лучи пересеклись в точке b, следова­тельно, точка е совпала с точкой b, поэтому p_ve=p_vb, be = 0, т. е. _E = _B, v_EB =0, = v_EB / = 0, сито 3 движется посту­пательно и v₃ = v_B.

Угловые скорости остальных ведомых звеньев:

= v_BA / = 2,513 /0,8 = 3,141 с^-1;

= = v_B/ = 2,513 / 0,5 = 5,026 .

Переходим к определению ускорений.

Поскольку кривошип OA вращается равномерно, ускорение его пальца А равно нормальному ускорению

= =2,513² / 0,2 = 31,576 м/с².

Для точки В, принадлежащей шатуну АВ,

= + = + + (3)

где вектор направлен вдоль ВС к центру С; вектор ВС; вектор направлен вдоль ВА к центру А; вектор АВ.

Находим величины нормальных ускорений:

= = = 12,63 м/с²;

= = 3,141² 0,8 = 7,893 м/с².

Графическое решение уравнения (3) показано на рис. 13.17, г. Выбрав направления осей координат так, чтобы ось x была параллельна шатуну АВ, проецируем уравнение (3) на эти оси:

sin 30° + = cos 30° = а_А sin 30° + ;

cos 30° - sin 30° = - а_А cos 30° + ,

откуда

= (а_А sin30° + - sin30°) / cos30° =

= (31,576 sin 30° + 7,893 -12,63 sin 30°) / cos 30° = 20,053 м/с²;

= (а_А + ) cos 30° - sin 30° =

= (31,576 +12,63) cos 30° - 20,053 sin 30° = 28,257 м/с².

Полное ускорение точки В

А_B = = = 23,69 м/с².

Ускорение точки Е

. (4)

Но = 0, поэтому = 0; ₄ = и = , следователь­но, = ; кроме того, || . Решая уравнение (4) с уче­том указанных условий, для чего достаточно его спроецировать на горизонтальную ось, получаем = и = 0, это значит, что = 0, т. е. сито движется поступательно (а не мгновенно поступательно) и его ускорение = = = 23,69 м/с². Угловые ускорения звеньев 2 и 4:

= / = 28,257 / 0,8 = 35,321 ;

= / = 20,053 / 0,5 = 40,106 .

Ответ: v₃ = ≈ 2,51 м/с; = = 23,69 м/с². 3,14 .

≈ 35,321 ; ₄ ≈ 5,03 ; 40,11 .

13.18. Кривошип OA механизма щековой дробилки вращает­ся с частотой n = 300 ми . Для положения, изображенного на рис. 13.18, а, определить угловую скорость и угловое ускорение щеки АВ и ускорение точки В, если = 1,0 м, = 0,012 м, = 0,45 м.

a б в

Решение. Скорость пальца А кривошипа

v_A = _OA = = = 0,377 м/с.

30

Траектория точки А - окружность радиусом OA, траектория точки В - дуга окружности радиусом СВ. Векторы скоростей этих точек, касательные к соответствующим траекториям, показаны на рис. 13.18, б. Восставив перпендикуляры из рассматриваемых точек к векторам их скоростей, находим МЦС щеки А В (точка ). Для определения скорости v_BA точки В относим последнюю к щеке АВ и применяем теорему о проекциях скоростей:

v_A cos 70° = v_B cos 45°,

откуда

v_B = v_A cos 70° / cos 45° = 0,377 cos 70° / cos 45° = 0,182 м/с.

Угловую скорость щеки АВ находим с помощью МЦС, предварительно из треугольника АВ определив по теореме синусов полюсное расстояние В = sin 20° / sin 115°.

Тогда

_OA = v_B / B = (v_B sin 115°) / ( sin 20°) =

= (0,182 sin 115°) / (1,0 sin 20°) = 0,483 .

Поскольку кривошип OA вращается равномерно, ускорение его пальца А равно нормальному ускорению , причем

= / = 0,377² / 0,012 = 11,844 м/с².

Для точки В, принадлежащей щеке АВ,

(1)

где вектор направлен вдоль ВС к центру С; вектор ВС; вектор направлен вдоль ВА к центру А; вектор АВ.

Находим величины нормальных ускорений:

= / = 0,182² / 0,45 = 0,074 м/с²;

= = 0,483² 1,0 = 0,233 м/с².

Графическое решение уравнения (1), т. е. план ускорений механизма, показано на рис. 13.18, е.

Выбрав направления осей координат так, чтобы ось была перпендикулярна вектору (рис. 13.18, е), проецируем уравне­ние (1) на эти оси:

= cos 25° - sin 45° + cos 45°;

= - sin 25° + cos 45° + sin 45°;

Откуда

= ( + sin 25° - cos 45°)/ sin 45° =

(0,074 +11,844 sin 25° - 0,233 cos 45°) / sin 45° = 6,95 м/с²;

= cos 25° - sin 45° + + cos 45° =

= -11,844 cos 25° - 0,233 sin 45° + 6,95 cos 45° = 15,484 м/с².

Полное ускорение точки B

= = 15,484 м/с².

Угловое ускорение щеки:

= / = 6,95 / 1,0 = 6,95 .

Ответ: _AB 0,48 с^-1; = 6,95 ; = 15,48 м/с².

1 3.19. Кривошип OA механизма шагания экскаватора-драг­лайна (рис. 13.19, а) вращается с частотой n = 3 мин^-1. Для поло­жения, показанного на рисунке, определить скорость и ускорение точки С лыжи, а также угловую скорость и угловое ускорение звена АВ, если = 2,0 м, = 0,5 м, = 1,2 м, = 1,75 м.

Решение. Скорость пальца А кривошипа

v_A = _OA = = = 0.157 м/с.

Траектория точки А — дуга окружности радиусом OA, Траектория точки В - дуга окружности радиусом BD. Векторы скоростей этих точек, касательные к соответствующим траекториям, показаны на рис. 13.19, б. Восставив перпендикуляры из рассматриваемых точек к векторам их скоростей, находим МЦС звена АВ

(точка ) .Для определения скорости v_B точки В относим последнюю к звену АВ и применяем теорему о проекциях скоростей:

v_A cos 0° = v_B cos 45°, откуда

v_B = (v_A cos 0°) / cos 45° = (0,157 cos 0°) / cos 45° = 0,222 м/с.

Угловую скорость звена АВ находим с помощью МЦС, пред­варительно из равнобедренного прямоугольного треугольника АВР_AB определив полюсное расстояние Р_AB А = _АВ.

Тогда

_AB = v_A / Р_AB А = v_A / _АВ = 0,157 / 2 = 0,0785 с ^-1.

Полюсное расстояние точки С определяем из треугольника АСР_AB по теореме косинусов:

Р_ABС =

= = 2,8м.

Скорость точки С: v_C = ( _AB (Р_АB С) = 0,0785 2,8 0,21 м/с. Поскольку кривошип ОА вращается равномерно, ускорение _А его пальца А равно нормальному ускорению а_АО. причем

= / _OА = 0,157²/0,5 = 0,049 м/с².

Для точки В, принадлежащей звену АВ,

, (1)

где вектор направлен вдоль ВD к центру D; вектор ВD; вектор направлен вдоль ВА к центру А; вектор АВ.

Находим величины нормальных ускорений:

= / _BD = 0,222 ² / 1,75 = 0,028 м/с²;

= _AB = 0,0785² 2 = 0,012 м/с².

Графическое решение уравнения (1), т. е. план ускорений звена АВ, показано на рис. 13.19, е. Выбрав координатные оси так, чтобы ось была горизон­тальна (рис. 13.19, в), проецируем уравнение (1) на эти оси:

cos45° + sin45°= а_А - ;

- sin45° + cos45° = - ,

откуда

= (- + sin 45°) / cos 45° =

= (-0,012 + 0,028 sin 45°)/ cos 45° = 0,011м/с²;

= - cos45° - sin45° + a_A =

= - 0,028 cos 45° - 0,011 sin 45° + 0,049 = 0,021 м/с².

Угловое ускорение звена АВ:

= _AB =0,021 / 2 0,011c^-2.

Ускорение точки С

(2)

где вектор направлен вдоль СА к центру A, = _AB =

= 0,0785² 1,2 = 0,074 м/с²; вектор АС, = _AC =

= 0,011 1,2 = 0,013 м/с².

Проецируя уравнение (2) на оси координат и подставляя найденные величины, получаем

= + sin 30° + cos30° =

= 0,049 + 0,0074 sin 30° + 0,013 cos 30° = 0,064 м/с²;

= cos 30° - sin 30° =

= 0,0074cos30° - 0,013 sin 30° = -0,0001 м/с².

Полное ускорение точки С:

_C = = ≈0,064 м/с².

Ответ: v_c ≈ 0,21 м/с; а_с ≈ 0,064 м/с ;

_AB ≈ 0,08с^-1; 0,011 с^-2.

13.20. При выдвижении стрелы роторного экскаватора точка А движется равномерно со скоростью v_A = 0,3 м/с, точка С каната ВС неподвижна (рис. 13.20, а). Определить угловую скорость и угловое ускорение стрелы для указанного на рисунке положения, если ₁= 60 м, ₂ = 25 м.

Рис. 13.20

Решение. Траектория точки В - дуга окружности радиу­сом ВС. Стрела АВ совершает плоскопараллельное движение. Принимаем точку А, скорость v_A которой задана, за полюс, тогда векторное уравнение скорости точки В имеет вид

_{B A}+ _BA ,

где _B ВС, a _BA AB.

Графическое решение этого уравнения (план скоростей ме­ханизма) представляет собой равносторонний треугольник p_vab (рис. 13.20, б), поэтому v_A = v_B = v_BA = 0,3 м/с.

Угловая скорость стрелы

_AB = = = 5 10 ^-3 с^-1 .

Поскольку точка А движется равномерно, то v_A = const и а_А = 0, поэтому векторное уравнение ускорения точки В, при­надлежащей звену АВ, имеет достаточно простой вид:

, (1)

где вектор нормального ускорения направлен вдоль ВС к цен­тру С; вектор тангенциального ускорения ВС; вектор нор­мального ускорения направлен вдоль ВА к центру А; вектор тангенциального ускорения АВ.

Находим величины нормальных ускорений:

= / _BD = 0,3² / 25 = 3,6 ^-3 м/с²;

= _AB = 0,3² /60 = 1,5 ^-3 м/с²;

Графическое решение уравнения (1), т.е. план ускорений стрелы АВ, показано на рис. 13.20, е.

Выбрав координатные оси так, чтобы ось была параллель­на продольной оси стрелы (рис. 13.20, в), проецируем уравнение (1) на эти оси:

cos 60° - sin 60° = ;

sin 60° + cos 60° = ,

откуда

= (- + cos 60°) / sin 60° =

= (-1,5 10^-3 + 3,6 10^-3 cos 60°) / sin 60° = 3,464 10 ^{- 4} м/с²;

= sin 60° + cos 60° =

= 3,6 10^-3 sin 60° + 3,464 10 ^{- 4} cos 60° = 3,291 10 ^{- 3} м/с².

Угловое ускорение стрелы:

= / _AB =3,291 10^-3/60 = 5,485 10^{- 5} с^-2 .

Ответ: _AB= 5 10^-3 с^-1; 5,5 10^-5 с^-2.

13.21. Кривошип OA механизма шагания экскаватора-драг­лайна (рис. 13.21, а) вращается с частотой n = 5 мин^-1. Для по­ложения, показанного на рисунке, определить ускорение точки В, а также угловую скорость и угловое ускорение звена ВС, если _OA = 0,4 м, _AB = 1,2 м, _AC = 1,6 м.

а б

Рис 13.21 а,б

Решение. В рассматриваемом механизме точка А движет­ся по дуге окружности радиусом OA, точка В - по так называе­мой шатунной кривой, а точка С - прямолинейно по вертикаль­ной прямой ОС. Скорость пальца А кривошипа

30

v_A = _OA = = = 0.209 м/с.

причем OA, т. е. вектор направлен вертикально вниз. Но и вектор скорости точки С тоже вертикален. Следовательно, МЦС звена ВАС находится в бесконечности, движение этого зве­на - мгновенно поступательное, его угловая скорость _BC = 0 и = = .

Поскольку кривошип OA вращается равномерно, а угловая скорость шатуна АС равна нулю, то = 0, = 0 и ускорение отнесенной к шатуну прямолинейно движущейся точки С:

= + ,

где вектор направлен по прямой ОС, вектор - по прямой АО к центру О, вектор АС. Величина нормального уско­рения

= = 0,209² / 0,4 = 0,109 м/с².

Обозначим угол наклона шатуна ВС к вертикали ОС через а, тогда sin α = =0,4 / 1,6 = 0,25; α 14,48°; cos α = 0,9682.

Проецируя векторное уравнение ускорений на горизонталь­ную ось, получаем 0 = - cos а, откуда

= / cos α = 0,109 / 0,9682 = 0,113 м/с².

Угловое ускорение шатуна ВС:

= =0,113 / l,6 = 0,071c^-2.

Теперь можно определить ускорение точки В из уравнения

= + ,

для чего спроецируем это уравнение на горизонтальную и верти­кальную координатные оси, учитывая, что AB и = = 0,071 1,2 0,085 м/с²:

= + cos α = 0,109 + 0,085 0,9682 = 0,191 м/с²;

= sin α = -0,085 0,25 = - 0,021 м/с².

Полное ускорение точки В:

= = = 0,192 м/с².

Для наглядности на рис 13.21, б показан план ускорений механизма, представляющий собой графическое решение уравнений (1) и (2) в некотором масштабе μ_a ( )

Ответ: а_B 0,19 м/с² ; _BC = 0; 0,07 с ^-2.

13.22. При повороте самосвала точка А прицепа движется равномерно с известной скоростью = , причем вектор образует с осью прицепа угол α, изменяющийся по закону α = kt, где k = const (рис. 13.22, а). Определить угловую скорость и угловое ускорение прицепа, а также ускорения точек А и

В, если известно, что скорость точки В в любом положении прицепа направлена по его продольной оси; АВ = .

Указание: радиус кривизны траектории точки В определяется по

формуле ρ = = = где - угловая скорость прицепа.

a б

Рис. 13.22

Решение. МЦС Р_AB прицепа находится на пересечении перпендикуляров, восставленных из точек А и В к векторам ско­ростей этих точек (рис. 13.22, б). Полюсное расстояние точки А

АР_АВ= АВ / sin α = / sin kt.

Угловая скорость прицепа

=v_A / AP_AB = v / ( / sin kt) = (v sin kt ) / ,

его угловое ускорение

= d / dt = = (kv cos kt) / l.

Точка А движется равномерно по некоторой кривой линии, следовательно, ускорение этой точки равно ее нормальному ус­корению:

a_A = =v²_A / ρ _A=v²/ ρ _A.

Радиус ρ _A кривизны траектории точки А находим по анало­гии с радиусом кривизны траектории точки В (см. указание в

условии задачи), учитывая, что угол ψ между касательной в точ­ке А к траектории этой точки и координатной осью Ох равен ψ = α + (см. рис. 13.22, б):

ρ_A = = = = =

dt

Тогда a_A = v ( k + ).

Ускорение a_B точки В складывается из нормального ускорения ⁼ / ρ_B касательного (тангенциального) ускорения = dv_B / dt.

Скорость v_B точки В находим, используя теорему о проек­циях скоростей:

v_B = v_A cos a = v cos kt.

Радиус ρ_B кривизны траектории точки В (в соответствии с указанием в условии задачи)

ρ_B = = = l ctg kt.

Ictgkt.

Рл =

Следовательно,

= = ;

= _B = -k sin kt.

Полное ускорение точки В

a_B = = =

=[( )/ ] .

Ответ: = ( sin kt) / ; = (kv cos kt) / ;

a_A = (k + ); а_B =[( sin kt) / ] .

13.24. В задаче 10.22 определить проекции скорости и уско­рения точки В на оси Ох и Оу, применяя теорию плоскопарал­лельного движения.

Р ешение. В начальном по­ложении (при β = 0) стержень АВ вертикален, точка М₁ шестерни / совпадает с точкой М₂ неподвижно­го колеса 2 (рис. 13.24).

В некотором промежуточном положении точка Р - полюс за­цепления шестерни 1 и колеса 2,

РМ₁ = РМ₂ , т.е. r₁ψ = r₂φ. Но r₁ = z r; φ = t; r₂ = r + r₁ = r (1 + z), поэтому z r ψ = r (1 + z) t, откуда

ψ = (1 + z) t / z.

Угол поворота сателлита

Рис 13.34 β = ψ – φ = .

Угловая скорость сателлита , его угловое ускорение .

Скорость точки В:

_A = _B = _BA,

где _A OA, v_A= r; _BA AB, v_BA = R = ( / z)R.

Проекции вектора v_B на координатные оси:

v_Bx = v_A cos φ + v_BA cos β = [r cos t + (R / z) cos ( t / z)];

v_By ⁼ v_A sin φ - v_BA sin β = [r sin t - (R / z) sin ( t / z)];

Ускорение точки В

,

так как = 0 и = 0, поскольку = const и = const, т. е. = 0 и = 0.

Вектор направлен вдоль АО к центру О; = ; вектор

направлен вдоль BA к центру А; = R= ( / z)² R.

Проекции вектора на координатные оси:

a_Bx = -a_A sin φ - a_BA cos β = [r sin t + (R / z²) sin ( t / z)];

a_By ⁼ a_A cos φ - a_BA cos β = [r cos t - (R / z²) cos ( t / z)];

Ответ: v_Bx = [r cos t + (R / z) cos ( t / z)];

v_By [r sin t - (R / z) sin ( t / z)];

a_Bx [r sin t + (R / z²) sin ( t / z)];

a_By = [r cos t - (R / z²) cos ( t / z)];

////////////////////////////////////////////////////////////////////////////////