
- •Решений задач по теоретической механике
- •Часть 2. Кинематика
- •Сборник решений задач подготовлен к размещению в сети интернет студентами группы асп-1-07 Маминовой т.Ю. И Скворцовым е.Д. Под руководством проф. Алюшина ю.А. В 2012 году
- •Глава 10 Кинематика точки
- •10.1. Прямолинейное движение точки
- •10.2. Криволинейное движение точки
- •Глава 11 Вращательное движение тела
- •Глава 12 Передачи
- •Глава 13 ///////////////////////////////////////////////////////////////////////////////////
- •Глава 14 Сложное движение точки
- •Глава 15 //////////////////////////////////////////////////////////////////////////////////////////////////////////
- •Глава 16 ////////////////////////////////////////////////////////////////////
- •Часть 2. Кинематика
- •Сборник решений задач подготовлен к размещению в сети интернет студентами группы асп-1-07 Маминовой т.Ю. И Скворцовым е.Д. Под руководством проф. Алюшина ю.А. В 2012 году
10.2. Криволинейное движение точки
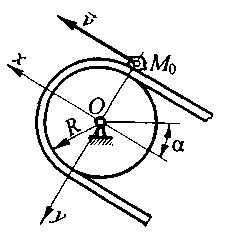
 0.10.
Лента конвейера движется
со скоростью v
под углом α к горизонту, огибая барабан
радиусом R
(рис. 10.10).
Кусок угля, принимаемый за материальную
точку М, отрывается
от ленты в положении М0
и далее совершает свободное
падение. Определить радиус ρ кривизны
траектории свободного
падения в начальной точке Мо.
Найти условие
отрыва куска. Толщиной ленты
и сопротивлением воздуха пренебречь.
0.10.
Лента конвейера движется
со скоростью v
под углом α к горизонту, огибая барабан
радиусом R
(рис. 10.10).
Кусок угля, принимаемый за материальную
точку М, отрывается
от ленты в положении М0
и далее совершает свободное
падение. Определить радиус ρ кривизны
траектории свободного
падения в начальной точке Мо.
Найти условие
отрыва куска. Толщиной ленты
и сопротивлением воздуха пренебречь.
Решение. В момент отрыва куска вектор его скорости направлен по касательной к внешней окружности барабана с лен-той, т. е. параллельно прямолинейному участку ленты.
Проекции этого вектора на оси хОу:

Дальнейшее движение точки М представляет собой свободное падение и поэтому происходит с ускорением g силы тяжести; проекции этого ускорения на те же оси:


Радиус кривизны траектории в точке М0 находим из второй формулы (10.11):

При отрыве куска угля от ленты радиус ρ кривизны траектории полета куска больше радиуса R внешней окружности ленты, огибающей барабан. Следовательно, условие отрыва куска:

Ответ:
 ,
где g
- ускорение свободного падения.
,
где g
- ускорение свободного падения.
Условие
отрыва:
 > R,
или
> R,
или
 .
.
10.11. Используя условие и ответ задачи 10.10, составить уравнение свободного падения материальной точки М в осях Оху и определить условия, при которых эта точка не упадет на барабан.
Решение. Движение происходит с постоянным по величине и направлению ускорением свободного падения; проекции этого ускорения на оси координат:
ах = - g sin a = const; ay = g cos a = const,
следовательно, вдоль оси Ох точка движется равнозамедленно, а вдоль оси Оу – равноускоренно. Обращаем внимание на то, что отмеченное выше постоянство величины и направления ускорения точки и его проекций не означает, что движение точки вдоль её параболической траектории является равнопеременным, так как условием равнопеременного движения является не а = const,
а аτ = const. В рассматриваемом случае касательное ускорение точки не является постоянным, в чем можно убедиться, если воспользоваться формулой (10.15).
Проекции начальной скорости:

Поскольку движение точки вдоль обеих осей координат является равнопеременным, то уравнения движения в проекциях на эти оси определяем по формуле (10.17), учитывая, что при t = 0
 a
a



Определим теперь условия, при которых точка упадет на барабан.
Очевидно,
что прежде чем упасть на барабан, точка
должна сначала оторваться от него, иначе
никакого падения не будет. Как показано
в решении предыдущей задачи, отрыв
происходит при
,
т. е. при
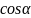 <
< .
.
После
отрыва точки от барабана ее траектория
не должна пересечь внешнюю окружность
барабана с лентой, поэтому расстояние
r
от начала координат до точки, равное

должно быть больше R в любой момент времени.
Чтобы
пересечение (или касание) стало возможным,
нужно иметь
 R.
Оба
этих параметра существенно положительны,
поэтому справедливо и неравенство
R.
Оба
этих параметра существенно положительны,
поэтому справедливо и неравенство
 2
R2,
или
х2
+ у2
R2.
Подставляя
в это неравенство значения х
и
у
из
уравнений движения куска, получаем
2
R2,
или
х2
+ у2
R2.
Подставляя
в это неравенство значения х
и
у
из
уравнений движения куска, получаем

или



Корни уравнения будут действительными, если

Поскольку
>
0, так как 0 <
 < 90°, то, разделив полученное неравенство
на
,
получаем gR
-
< 90°, то, разделив полученное неравенство
на
,
получаем gR
-
 >
0 и
< gR/v2.
Последнее
неравенство является условием
падения куска на барабан. А
чтобы падения на барабан не было, нужно,
наоборот, иметь
> gR/v2.
Окончательно условия, при которых точка
не упадет на барабан, приобретают вид
>
0 и
< gR/v2.
Последнее
неравенство является условием
падения куска на барабан. А
чтобы падения на барабан не было, нужно,
наоборот, иметь
> gR/v2.
Окончательно условия, при которых точка
не упадет на барабан, приобретают вид

Ответ: ;
;

Рис.
10.12
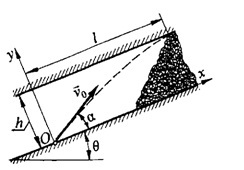
 0.12.
На каком расстоянии l
от конвейера необходимо установить
углеотбойный щит (рис. 10.12), чтобы кусок
угля, отрывающийся от конвейера со
скоростью v0
= 3 м/с под углом 10° к горизонту, ударился
о щит на расстоянии h
= 1 м ниже
места вылета. Определить скорость
v1
куска
угля в момент удара.
0.12.
На каком расстоянии l
от конвейера необходимо установить
углеотбойный щит (рис. 10.12), чтобы кусок
угля, отрывающийся от конвейера со
скоростью v0
= 3 м/с под углом 10° к горизонту, ударился
о щит на расстоянии h
= 1 м ниже
места вылета. Определить скорость
v1
куска
угля в момент удара.
Решение.
Совмещаем начало координат О
системы
хОу
с
положением куска угля в момент отрыва
этого куска от ленты конвейера (рис.
10.12), направляя оси координат так, как
показано на рисунке. После отрыва
кусок совершает свободное падение при
начальной скорости
 .
.
Начальные координаты куска угля:

проекции его начальной скорости на оси координат:

проекции ускорения:

Отсюда видно, что вдоль оси Ох исследуемая точка (кусок угля) движется равномерно, а вдоль оси Оу – равноускоренно.
Уравнения для определения проекций скорости и ее полной величины в произвольный момент времени получаем на основе формул (10.18) и (10.7):



Уравнения движения точки в соответствии с формулами (10.16) и (10.17):

Чтобы найти время t1 движения точки до удара, в последнее уравнение подставляем у = h:

откуда


Зная
время
 ,
можно
определить расстояние l
до углеотбойного щита и скорость v1
куска в момент удара о щит:
,
можно
определить расстояние l
до углеотбойного щита и скорость v1
куска в момент удара о щит:



Ответ:

Рис. 10.13

Решение.
После вылета из ковша кусок породы,
принимаемый за материальную точку
М, совершает свободное падение с
ускорением
 (ускорение силы тяжести) и начальной
скоростью
.
В принятой на рис. 10.13 системе отсчета
начальные координаты точки, проекции
ее начальной скорости и полного ускорения
на оси координат равны
(ускорение силы тяжести) и начальной
скоростью
.
В принятой на рис. 10.13 системе отсчета
начальные координаты точки, проекции
ее начальной скорости и полного ускорения
на оси координат равны



Проекции ускорения постоянны по величине, следовательно, как вдоль оси М0х, так и вдоль оси М0у движение точки равнопеременное.
Уравнения движения в соответствии с формулой (10.17) принимают вид
х = v0t
sin
 ;
(1)
;
(1)
у = v0t
cos .
(2)
.
(2)
Чтобы найти дальность L полета куска породы, определим сначала время t1 падения этого куска на ленту конвейера, для чего в уравнение (1) подставим х = h:

или

откуда


Дальность L полета куска породы вычисляем из уравнения (2) при t = t1:




Чтобы падающий на ленту кусок не проскальзывал по ленте при падении на нее, необходимо равенство скорости v ленты и проекции vy скорости куска на ось M0y при t=t1:




Ответ:

где γ=α+θ=25 ,
,
Скорость ленты

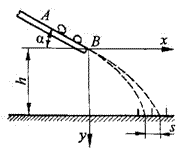
Рис.
10.14
Решение.
После
срыва с наклонной плоскости движение
обоих кусков руды является свободным
падением с начальной скоростью
 ,
направленной вправо-вниз под углом α
к оси Вх.
,
направленной вправо-вниз под углом α
к оси Вх.
Ускорение свободного падения ориентировано вертикально вниз, его проекции на оси координат в принятой на рис. 10.14 системе отсчета:
Следовательно, кусок руды движется равномерно вдоль оси Вх и равноускоренно вдоль оси By.
Начальное положение куска определяется координатами х0 = 0 и у0 = 0, проекции начальной скорости на оси координат равны: vx 0 = v0 cos α и vy 0 = v0 sin α. Пользуясь формулами (10.16) и (10.17), можем записать уравнения движения в виде

Тогда
для первого куска руды при дальности
полета x1= и
высоте падения у1=
h
за
время t1
будем
иметь
и
высоте падения у1=
h
за
время t1
будем
иметь

Подставляя найденное из первого уравнения выражение для во второе, получаем квадратное уравнение, решение которого
имеет вид

Совершенно аналогично для второго куска руды имеем

Куски руды упадут друг от друга на расстоянии




Ответ:
s


Рис 10.15, а
10.15*. При водопадном режи- ме движения загрузки в шаровой мельнице (рис. 10.15, а) шар М, перемещавшийся вместе с бараба- ном, отделяется от стенки послед- него в точке А, положение которой определяется центральным углом а = arccos (Rω2/g), где ω - угловая скорость барабана, R - его радиус, g - ускорение свободного падения. Скорость шара в момент отрыва
v0 = ωR. Дальнейшее движение шара М по траектории АBС заканчивается ударом о стенку барабана в точке С. Найти уравнение траектории шара в осях Аху, его скорость, тангенциальное и нормальное ускорения и радиус кривизны траектории в функции времени t. Определить также время t1 движения шара от момента отрыва до удара, угол β, показывающий положение точки С, и скорость v1 шара в момент падения на стенку.
Решение. Движение шара после отделения от стенки барабана - это свободное падение с ускорением g и начальной скоростью v0. Составляем уравнение этого движения в системе отсчета хАу, считая шар материальной точкой.
 *
Краткое
решение этой задачи с использованием
уравнений в безразмерной форме приведено
[1]. Здесь дастся более простое, но и более
пространное решение.
*
Краткое
решение этой задачи с использованием
уравнений в безразмерной форме приведено
[1]. Здесь дастся более простое, но и более
пространное решение.
Проекции начальной скорости:

проекции ускорения:

Следовательно, проекция точки М на ось Ах движется равномерно, а проекция на ось Ау - равнозамедленно, т. е.
 (1)
(1)
Для вывода уравнений движения используем зависимость (10.5) проекций скорости от координат:
vx
=
 =
dx/dt, vy
=
=
dx/dt, vy
=
 =
dy/dt,
=
dy/dt,
огкуда
 (2)
(2)
Подставляем в уравнения системы (2) х0 = 0 и у0 = 0 (поскольку начало траектории свободного падения шара расположено в начале координат) и значения vx и vy, из системы уравнений (1). Интегрируя, получаем уравнения движения точки М в параметрической форме:
 (3)
(3)
Чтобы
перейти к уравнению траектории в виде
зависимости
 ,
исключаем из системы (3) время t.
Для этого найденное из первого уравнения
этой системы время t
подставляем
во второе
уравнение:
,
исключаем из системы (3) время t.
Для этого найденное из первого уравнения
этой системы время t
подставляем
во второе
уравнение:

или, учитывая, что по условию α = arcos (Rω2/g) и v0 = ωR, т. е. ω2 = (g cos α) / R и v02 = Rg cos α, имеем
 (4)
(4)
Поскольку
всякое уравнение типа у
= Ах2
+ Вх + С графически
изображается параболой, то и полученное
уравнение (4) есть уравнение параболы
при A=-1/(2R
 ,
B=tg
,
C=0.
,
B=tg
,
C=0.
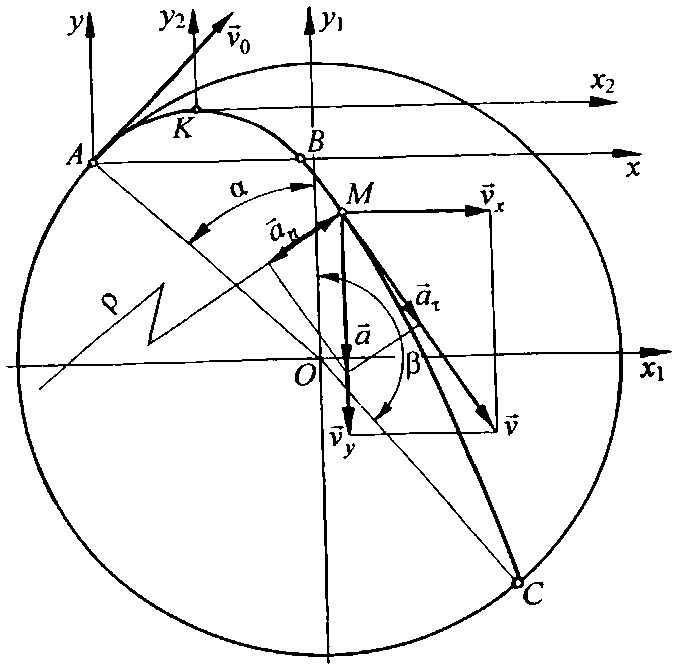
Рис.
10.15, б
Если перенести начало координат в вершину параболы (точка К на рис. 10.15, б), то в системе отсчета х2Ку2 уравнение траектории примет более простой вид.
Координаты вершины параболы находим из условия, что в этой точке при t = tK вертикальная проекция скорости vy = 0 (шар перестает набирать высоту). Тогда из второго уравнения системы (1) получаем
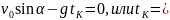
Подставляем найденное значение tK в уравнения (3):



К этому же результату приходим, используя общую теорию параболы (см., например, [4, § 50]), согласно которой


Теперь после подстановки x = x2 + хк и у = y2 + ук в уравнение (4) и несложных преобразований уравнение траектории шара в системе отсчета х1Ку1 принимает вид

Вид траектории показан на рис. 10.15, б.
Модуль скорости шара

 (5)
(5)
Полное ускорение а шара известно: a=g.
Касательное ускорение

Из
этой формулы видно, что
 const,
следовательно, хотя полное ускорение
точки а
= g
=
const,
ее движение не является равнопеременным,
так как условием равнопеременного
движения является
постоянство касательного, а не полного
ускорения.
const,
следовательно, хотя полное ускорение
точки а
= g
=
const,
ее движение не является равнопеременным,
так как условием равнопеременного
движения является
постоянство касательного, а не полного
ускорения.
Нормальное ускорение шара

Радиус кривизны траектории

Положение точки С находим, вычислив сначала время движения t1 шара до момента падения на стенку барабана. Для этого представим уравнения (3) в несколько ином виде, принимая во внимание, что v0 = ωR и g = Rω2 / cos α:
 (6)
(6)
При t = t1 эти координаты определяют положение точки М на окружности барабана. Уравнение окружности в системе хАу:
 .
(7)
.
(7)
После
подстановки (6) в (7), раскрытия скобок,
приведения подобных и сокращения на
 0
получаем уравнение для определения
времени движения t1:
0
получаем уравнение для определения
времени движения t1:

из которого имеем
 (8)
(8)
Координаты точки С в системе хАу определяем из уравнений (6) при t = :

Координаты этой же точки в системе Х1Оy1:

Угол, определяющий положение точки С на внутренней поверхности барабана,

Скорость шара в момент его падения на барабан определяем по формуле (5) при t = t1 :



Ответ:





10.16. Частица руды (материальная точка М) скатывается с постоянной по модулю скоростью v по поверхности винтового спуска, оставаясь все время на расстоянии R от его оси (рис. 10.16). Составить уравнение движения частицы в декартовых координатах и найти ее ускорение, если в начальный момент она находится на оси Ох, а угол подъема винтовой линии, по которой движется частица, равен α. Определить радиус ρ кривизны винтовой линии.
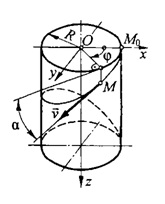 Решение.
Частица руды движется равномерно по
винтовой линии, расположенной на
поверхности кругового цилиндра радиусом
R.
Угол
ф, определяющий положение точки М,
отсчитываем
от оси Ох,
на
которой (в точке Мо)
находилась
частица в начальный момент времени.
Решение.
Частица руды движется равномерно по
винтовой линии, расположенной на
поверхности кругового цилиндра радиусом
R.
Угол
ф, определяющий положение точки М,
отсчитываем
от оси Ох,
на
которой (в точке Мо)
находилась
частица в начальный момент времени.
Рис.
10. 16
 скорости
на эту плоскость, причем
скорости
на эту плоскость, причем
 cos
α
= const,
так s
= vxyt=vt
cos
α.
В то же время длина дуги окружности
s
=
cos
α
= const,
так s
= vxyt=vt
cos
α.
В то же время длина дуги окружности
s
= .
Следовательно, vt
cos
α
=
,
откуда
.
Следовательно, vt
cos
α
=
,
откуда
 = (vt
cos
α)
/ R.
= (vt
cos
α)
/ R.
Вдоль вертикальной оси Oz проекция частицы движется также равномерно, поскольку проекция скорости на вертикаль vz = v sin α = const.
Теперь можно найти координаты частицы в произвольный момент времени, т. е. уравнения ее движения в координатной форме:
х = R cos = R cos [(vt cos α) / R],
у = R sin = R sin [(vt cos α) /R],
z = vzt = vt sin α.
Проекции скорости и ускорения частицы [по формулам (10.5) и (10.6)]:
vx=dx/dt = - v cos α sin [(vt cos α) / R],
vy = dy/dt = v cos α cos [(vt cos α) / R],
vz = dz/dt = v sin α;
ax= dvx / dt = - (v2/ R) cos2 a cos [(vt cos α)/R)],
ay=dvy / dt = - (v2/ R) cos2 a sin [(vt cos α) /R)],
az = dvt /dt = 0.
Полное ускорение по формуле (10.8):



Поскольку задано v = | | = const, то касательное ускорение = dv / dt = 0, а нормальное ускорение an равно полному. Отсюда следуег, что направления полного и нормального ускорений точки совпадают, т. е. полное ускорение частицы направлено по главной нормали к центру кривизны траектории в данной точке. Главная нормаль винтовой линии, расположенной на круговом цилиндре, перпендикулярна к оси винтовой линии и идет вдоль радиуса цилиндра (см. [4, § 359]), значит, ускорение точки М направлено к оси цилиндра перпендикулярно ей.
Радиус ρ кривизны траектории находим из второй формулы (10.11):
ρ = v2 / ап = v2 / а = v2 / [(v cos )2 / R]= R /cos2 .
Ответ: х = R cos , у = R sin , z = vt sin ,
где = (vt cos ) / R;
ускорение
a
=
 и
направлено к оси
и
направлено к оси
цилиндра перпендикулярно ей;
ρ = R /cos2 .
10.17. Частица закладочного материала, вылетающая из метательной машины со скоростью v0 = 11 м/с под углом = 30° к плоскости почвы, движется, испытывая сопротивление воздуха, согласно уравнениям
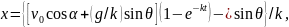

где g = 9,81 м/с2 - ускорение свободного падения, к =0,03 с-1 -удельный (отнесенный к единице массы) коэффициент сопротив-
Рис.
10.17
 ения
движению частицы, θ
= 25° - угол падения пласта (рис. 10.17).
Мощность пласта h
= 1,5 м. Выразить проекции ускорения
частицы через проекции ее скорости.
На каком расстоянии l
от закладки должно находиться место
вылета частицы, чтобы обеспечить ее
попадание под кровлю?
ения
движению частицы, θ
= 25° - угол падения пласта (рис. 10.17).
Мощность пласта h
= 1,5 м. Выразить проекции ускорения
частицы через проекции ее скорости.
На каком расстоянии l
от закладки должно находиться место
вылета частицы, чтобы обеспечить ее
попадание под кровлю?
Решение. Сначала по формулам (10.5) и (10.6) находим проекции скорости и ускорения на координатные оси Оху:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Выражаем проекции ускорения через проекции скорости, для чего из уравнения (1) определяем величину первого слагаемого правой части и подставляем ее в уравнение (3). Аналогичную операцию проделываем с уравнениями (2) и (4). Получаем
ах = - (kvx + g sin θ),
ау = - (kvy + g cos θ).
Попадание частицы под кровлю при заданных величинах скорости вылета v0 и угла α произойдет при условии, что верхняя точка траектории частицы находится на расстоянии ymax, равном пласта h, от подошвы выработки. Но если y=ymax, то производная dy/dt=vy=0 и из уравнения (2) имеем
 (5)
(5)
Подставляем (5) во второе уравнение движения при у = h.


откуда время полета частицы
 (6)
(6)
Теперь выражения (5) и (6) подставляем в первое уравнение движения при х = l, где l - расстояние от места вылета частицы до закладки под кровлю выработки, и после некоторых несложных преобразований получаем


Ответ: ах = - (kvx + g sin θ), ау = - (kvy + g cos θ);
1 0.18.
Угол
поворота φ ротора l
поршневого насоса изменяется по
закону φ = ωt
(ω
= const),
при этом поршни 2,
оси
которых расположены на расстоянии
R
от
оси ротора Oz,
опираются
на плоскость неподвижной шайбы 3,
наклоненной
под углом α
к оси Oz
(рис.
10.18). Составить уравнения движения
точки
М
поршня
в осях Oxyz
и
определить ее скорость
v,
тангенциальное
аτ
, нормальное
аn
и
полное
а
ускорения,
а также
радиус
ρ
кривизны
траектории.
Поперечными
размерами
поршня
пренебречь.
0.18.
Угол
поворота φ ротора l
поршневого насоса изменяется по
закону φ = ωt
(ω
= const),
при этом поршни 2,
оси
которых расположены на расстоянии
R
от
оси ротора Oz,
опираются
на плоскость неподвижной шайбы 3,
наклоненной
под углом α
к оси Oz
(рис.
10.18). Составить уравнения движения
точки
М
поршня
в осях Oxyz
и
определить ее скорость
v,
тангенциальное
аτ
, нормальное
аn
и
полное
а
ускорения,
а также
радиус
ρ
кривизны
траектории.
Поперечными
размерами
поршня
пренебречь.
Рис.
10.18
Решение. Координаты точки М в системе отсчета Oxyz:


Проекции векторов скорости и ускорения на те же оси:






Далее находим модули векторов скорости и ускорения по формулам (10.7) и (10.8):





Тангенциальное ускорение точки М:

Нормальное ускорение:


Радиус кривизны траектории


Ответ:






10.19. Рабочий орган виброконвейера совершает поступательные колебания в двух взаимно перпендикулярных направлениях (рис. 10.19, а), при этом любая его точка М движется согласно уравнениям

где
А,
В,
 и
и
 - константы. Определить траекторию,
скорость и ускорение точки М.
- константы. Определить траекторию,
скорость и ускорение точки М.
б
а

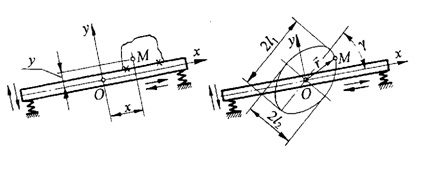
Рис.
10.19
Решение. Заданные уравнения движения точки М являются в то же время параметрическими уравнениями траектории. Для исключения параметра t находим значения функций sin ωt и cos ωt и подставляем их в тождество sin2 ωt + cos2 ωt = 1. Из второго уравнения движения имеем sin ωt = у / В. Первое уравнение представим в виде
х = A sin (ωt + ε) = A (sin ωt cos ε + cos ωt sin ε),
откуда

Тогда

или (после раскрытия скобок и приведения подобных)

В курсе аналитической геометрии доказывается, что всякое уравнение второго порядка есть уравнение либо эллипса, либо гиперболы, либо параболы, либо пары прямых (пересекающихся, параллельных или совпавших). В данном случае мы получили уравнение эллипса с центром в начале координат и полуосями l1 и l2, повернутыми относительно координатных осей на некоторый угол γ (рис. 10.19, б). Величины l1 и l2 и значение угла γ определены в [1, решение задачи 10.20*].
Проекции скорости точки М:


модуль скорости

Проекции ускорения точки М:


модуль этого ускорения:

Вектор
ускорения
 ,
где
,
где
 и
и
 - основные векторы (орты),
- основные векторы (орты),
 - радиус-вектор точки M.
Полученное выражение показывает, что
векторы а
и
направлены
в противоположные стороны, т. е. во всех
положениях точки М
вектор
ее ускорения направлен к началу координат.
- радиус-вектор точки M.
Полученное выражение показывает, что
векторы а
и
направлены
в противоположные стороны, т. е. во всех
положениях точки М
вектор
ее ускорения направлен к началу координат.
Ответ: Уравнение траектории (эллипса) –



вектор в любом положении точки направлен к началу
координат.
10.22. Кривошип OA механизма бесцепной подачи комбайна, вращаясь вокруг центра О, заставляет шестерню I обкатываться по неподвижному колесу 2, соосному с кривошипом (рис. 10.22). С шестерней l жестко связаны стержни, несущие ролики (цевки) В, число которых равно z. Цевки равномерно расположены на окружности радиусом lAB = R. Длина кривошипа 1OA=r, радиус подвижной шестерни r1 = zr, угол поворота кривошипа φ = ωt, причем ω = const. Составить уравнения движения точки В и определить ее скорость, ускорение и радиус Кривизны траектории. При φ = 0 точки А и В лежат на оси Оу.

неподвижного
колеса, т. е.
 PM1
=
PM2.
Но
PM1
=
PM1
=
PM2.
Но
PM1
=
 ψ,
а
ψ,
а
PM2
=
 ψ
= (
+ r)
φ,
где ψ
- угол поворота рычага ВС
относительно
кривошипа,
- радиус
начальной окружности колеса 2,
поэтому
ψ
= (z
+ 1)
φ , или
zrψ
= (zr
+ r)
φ, откуда
ψ
= (
+ r)
φ,
где ψ
- угол поворота рычага ВС
относительно
кривошипа,
- радиус
начальной окружности колеса 2,
поэтому
ψ
= (z
+ 1)
φ , или
zrψ
= (zr
+ r)
φ, откуда
ψ
= (z
+1) φ
/z
= (z
+1)
 /z.
/z.
Абсолютный угол поворота шестерни 1 и соединенного с нею рычага ВС:
 = ψ
- φ = (z
+1)
/z
-
=
/z.
= ψ
- φ = (z
+1)
/z
-
=
/z.
Теперь можно определить координаты точки В в системе отсчета хОу, т. е. составить уравнения движения этой точки в параметрической форме:
х
=
 sin
φ
+
sin
φ
+
 sin
= r
sin
+ R
sin
(
/z),
sin
= r
sin
+ R
sin
(
/z),
y
=
 cos
φ
+
cos
= -r
cos
+ R
cos
(
/z),
cos
φ
+
cos
= -r
cos
+ R
cos
(
/z),
Проекции скорости и ускорения точки на те же координатные оси находим по формулам (10.5) и (10.6):
 =
dx
/dt = r
cos
+ (R
/z) cos (
/z),
=
dx
/dt = r
cos
+ (R
/z) cos (
/z),
 =
dy
/dt = r
sin
+ (R
/z) sin (
/z);
=
dy
/dt = r
sin
+ (R
/z) sin (
/z);
ax = dvx /dt = - r 2 sin - (R 2 / z2) sin ( /z),
ay = dvy / dt = r 2 cos - (R 2 / z2) cos ( /z).
Скорость точки В:
 =
=
= =
=
=
 =
=

=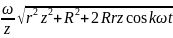 ,
где
,
где
 .
.
Ускорение точки В определяем, используя аналогичные преобразования. В результате получаем
 .
.
Радиус кривизны траектории найдем из второй формулы (10.11), предварительно вычислив нормальное ускорение по формуле (10.14):


Ответ: x = r sin + R sin ( /z),
y =r cos + R cos ( /z);
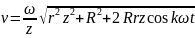 ;
;


10.24. Стрела OO1 (рис. 10.24) роторного экскаватора, расположенная в горизонтальной плоскости хОу, вращается вокруг
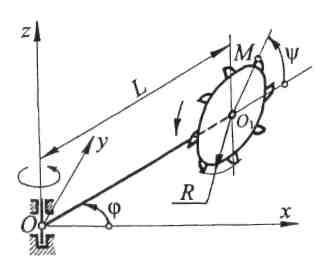
 ;
ротор
вращается относительно
стрелы
в плоскости zOO1
вокруг цен-
тра О1
по закону ψ=
;
ротор
вращается относительно
стрелы
в плоскости zOO1
вокруг цен-
тра О1
по закону ψ=
 ;
; и
и
 - постоянные. Вылет L
стре-
лы и радиус R
ротора известны.
Составить
уравнения движения
точки М,
находящейся на пери-
ферии
ротора, и определить ско-
рость
этой точки (скорость реза-
ния).
Чему равно максимальное
- постоянные. Вылет L
стре-
лы и радиус R
ротора известны.
Составить
уравнения движения
точки М,
находящейся на пери-
ферии
ротора, и определить ско-
рость
этой точки (скорость реза-
ния).
Чему равно максимальное
Рис. 10.24 значение этой скорости?
Решение. Составляем уравнения движения точки М в системе координат Oxyz в параметрической форме:
х = (L + R cos ψ) cos φ,
у = (L + R cos ψ) sin φ,
z = R sin ψ.
или (с учетом исходных данных)
х = (L + R cos ) cos ,
у = (L + R cos ) sin ,
z = R sin .
Проекции скорости находим по формулам (10.5):
x
= =
=

y
= =
=

z
= =
=
 .
.
Полная скорость равна

Максимального значения скорость точки М достигает при
cos = 1, т. е. при ψ = 0:

Ответ: х = (L + R cos ) cos ,
у = (L + R cos ) sin ,
z = R sin .


10.25. Водило OA планетарного рабочего органа проходческого комбайна,
Рис.
10.25 ,
где
'
=
,
где
'
=
 = =const
(рис. 10.25). Известны размеры
r
и R
= λr.
Составить уравнение
движения точки М (режущего
инструмента) и определить ее скорость
(скорость резания). Найти максимальное
значение этой скорости, если λ>1
и i
>1.
= =const
(рис. 10.25). Известны размеры
r
и R
= λr.
Составить уравнение
движения точки М (режущего
инструмента) и определить ее скорость
(скорость резания). Найти максимальное
значение этой скорости, если λ>1
и i
>1.
Решение. При составлении уравнений движения режущего инструмента в системе отсчета Oxyz сначала определяем координаты центра А режущего диска:
хА = R sin φ, уА = 0, zA = R cos φ ,
а затем находим координаты точки М:
х = хА + r cos ψ cos φ = R sin φ + r cos ψ cos φ,
y = yА + r sin ψ = r sin ψ,
z = zА + r cos ψ sin φ = R cos φ - r cos ψ sin φ.
Учитывая заданные зависимости углов φ и v от угловой скорости и времени t, а также соотношение между r и R, получаем



Из этих параметрических уравнений движения точки М по формулам (10.5) находим проекции ее скорости на координатные оси системы Oxyz:
x
= dx / dt =
r
( cos
cos
 -
i
sin
-
i
sin
 cos
- cos
sin
),
cos
- cos
sin
),
y=dy
/ dt =ir
cos
 ,
,
z = dz / dt = r ( sin + i sin sin - sin cos ),
а затем по формуле (10.7) вычисляем полную скорость:
 .
.
Максимум скорости соответствует максимуму подкоренного выражения f(t). Как известно, функция f(t) имеет в точке t = t1 максимум, если в этой точке первая производная df / dt = 0, а вторая производная d f2 /dt2 < 0 [4, § 276-279]. В рассматриваемом случае
df
/ dt
= 2
(sin
 + i
)
cos
= 0.
+ i
)
cos
= 0.
Корни этого уравнения, т. е. критические значения аргумента. соответствуют равенствам sin = i и cos = 0. По
условию X > 1 и i > 1, значит, i > 1. Но sin | | 1, следовательно, выражение sin = - i лишено смысла. Осталось исследовать второе критическое значение аргумента. Вторая производная
d2f
/ dt2
= 2i2 [sin
(sin
+ i
)
- cos2
].
[sin
(sin
+ i
)
- cos2
].
При cos = 0 получаем
d2f / dt2 = 2i2 [sin (sin + i )].
Выражение в круглых скобках при любых значениях t
больше нуля, поэтому d2f / dt2 < 0, если sin < 0. Следовательно, f(t) имеет максимум при cos = 0 и sin = -1, т. е. при = 3 π/ 2, а скорость при этой величине угла ψ имеет максимальное значение:

Ответ:
 .
.


