10.1. Прямолинейное движение точки

10.1. Разгон подъемного сосуда состоит из двух этапов: дви­жения с постоянным ускорением а₁ в течение времени t₁ из состояния покоя и дальнейшего движения с постоянным ускоре­нием a₂=0,8 м/с² в течение времени t₂ до достижения максимальной скорости 5,2 м/с (рис. 10.1). Путь h₁ за время t₁ равен 2 м, полное время разгона t=8 с. Определить величины t₁, (скорость в конце первого этапа), а₁, t₂, h₂ (перемещение сосуда за время t₂).

Р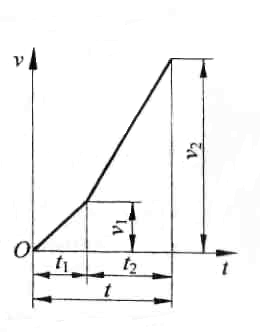 ешение. Начальная скорость v_I(0) сосуда на первом этапе равна нулю, так как движение начинается из состоя­ния покоя, а ускорение постоянно, сле­довательно, скорость сосуда нарастает по закону (0 ) и в конце этапа составляет величину . Пе­ремещение сосуда за время при рав­ноускоренном движении [см. формулу (10.17) при = 0 и = 0]

Рис. 10.1

(1)

На втором этапе (при ) движение тоже равноускоренное, но ₍₀₎ , следовательно,

В соответствии с графиком скорости (см. рис. 10.1) началь­ная скорость на втором этапе равна конечной скорости первого этапа, т. е. ₍₀₎ , поэтому в конце второго этапа, когда t_i = t,

(2)

Из уравнения (1) находим и подставляем в уравнение (2):

,

откуда

. (3)

Решая уравнение (3) и исключая отрицательное значение t₁ как неудовлетворительное, получаем

Теперь из формулы (1) находим ускорение сосуда на первом этапе разгона:

.

Скорость в конце первого этапа, когда t_i = t₁,

= = 0,414 3,11 1,29 м/с.

Продолжительность второго этапа:

4,89 с.

Перемещение сосуда за время t₂ при равноускоренном движении с ускорением а₂:

₍₀₎t₂+ /2=

=1,29 4,89+0,8

Ответ: t₁

t₂=4,89 c; h₂ 15,87 м.

Рис. 10.2

Рис. 10.2

Рис. 10.2

10.2 На расстоянии 42,8 м от верхней приемной площадки начина­ется торможение шахтной клети, дви­жущейся со скоростью V] = 10 м/с. Пе­риод торможения состоит из двух эта­пов: движения с постоянным замед­лением а=1,2 м/с² и равномерного движения (дотягивания) со скоростью v₂ = 0,5 м/с (рис. 10.2). Определить полное время торможения t_τ (до оста­новки клети).

Рис. 10.1

Решение. На первом этапе при равнозамедленном движении скорость изменяется но закону (10.18), поэтому время движения (с) на этом этапе

За это время клеть пройдет расстояние

Время второго этапа (дотягивания на расстояние S₂ с посто­янной скоростью )

Полное время торможения

Ответ: t_τ 10,4 с.

10.3. Ускорение клети в зависимости от времени t выражает­ся формулой а = а₀{1 - sin [πt/(2t)]}, где а₀ и t₁ - постоян­ные. Найти уравнения скорости и пути, зная, что = 0, а также выяснить механическое значение величин а₀ и t₁ и выразить t₁ через максимальную скорость подъема. После ближайшего мо­мента времени, для которого а = 0, подъем клети происходит равномерно.

Решение. Анализируя заданную функцию а = , находим, что при t = 0 ускорение а= а₀, следовательно, а₀- начальное значение ускорения клети; при t = t₁ ускорение а = а₀{1 - sin [πt/(2t)]}=a₀(1-sin π/2)=0, т. е. в этот момент заканчивается разгон и дальнейший подъем клети происходит равномерно, значит, t₁ - время ускоренного движения.

Из условия (10.6) или (10.11) имеем a = dv/dt, откуда

dv = adt. Поскольку при t = 0 = 0, то , или

Уравнение пути определяем из условия (10.10) : v = ds/dt, откуда ds= v dt.Поскольку при t=0 s=0, то , или

= .

Максимальная величина скорости достигается при t=t₁, так как в период разгона ускорение все время остается положительным (а , ибо 0 Следовательно,

,

откуда

.

Ответ: ;

;

– начальное ускорение клети

t₁=π – время ускоренного движения.

10.4. При торможении самосвала абсолютная величина за­медления машины в течение 0,8 с возрастает пропорционально времени от нуля до 3,2 м/с² и затем остается постоянной. Ско­рость самосвала в начале торможения равна 18 км/ч. Определить время торможения t₁ и тормозной путь s_T

Решение. В первый период торможения (0 t t₁ = 0,8 с) абсолютная величина замедления а возрастает от нуля до a_max пропорционально времени движения, т. е. а = с t, где с = а_тaх / t₁ -коэффициент пропорциональности.

Поскольку а= dv/dt, то dv = a dt = (a_max / t₁) dt.

Интегрируя это выражение при изменении скорости от до за период времени от 0 до t₁, находим значение скорости в конце первого периода:

Принимая во внимание, что скорость в начале торможения v₀ = 18 км/ч = 5 м/с, а максимальное замедление a_max= - 3,2 м/с², получаем

В течение второго периода торможения ( ), когда ве­личина замедления остается постоянной и равной а_тaх, скорость изменяется от до =0 по закону , поэто­му в конце периода 0 = , , следовательно, время торможения

Тормозной путь находим, учитывая, что в течение первого периода скорость изменяется по закону

=5 0,8+3,72 (1,9625 – 0,8)+

Ответ: t_T 1,96 c; s_T 5,82 м.

ик

10.5. Частица руды движется в сопротивляющейся среде прямолинейно по закону х = {и ln }/k, где и и к – посто­янные. Определить скорость v и ускорение а частицы и найти за­висимость а Выяснить механическое значение величины и.

Решение. Скорость частицы находим, дифференцируя по времени закон ее движения. Напомним, что производная нату­рального логарифма ; производная гиперболи­ческого косинуса ; производная гиперболиче­ского тангенса ; [4, § 243 и § 403].

Поскольку х = {и ln } / k, то

(1)

Производная скорости по времени есть ускорение частицы:

(2)

Чтобы найти зависимость ускорения от скорости, выразим функцию через th , учитывая, что ch² -sh² и что из уравнения (1) в данном случае th

Тогда

Подставив найденное выражение в формулу (2), получаем

Осталось выяснить механическое значение константы и. Для этого вспомним, что значения функции th х находятся в интерва­ле между -1 и +1, следовательно, на основании формулы (1) можно утверждать, что v < и, но при t th х 1, а скорость частицы , т. е. и - это предел скорости частицы руды.

Ответ: v=u th(kt); a=

u – предельная скорость частицы, u= .

10.6. Частица минерала в аппарате для обогащения руды падает в сопротивляющейся среде по закону s = u[t + (e^-kt -1)/k], где u и к постоянные. Найти зависимости v = f₁(t); и а f₂(t); выяснить механическое значение величины и.

Решение. Скорость и ускорение частицы находим, снача­ла дифференцируя по времени закон ее движения, а потом - по­лученный закон изменения скорости.

Поскольку s = u[t + (e^-kt -1)/k], то

(1)

(2)

Из формулы (1) находим , а затем, подставляя это выражение в формулу (2), получаем a=k (u-v).

Чтобы выяснить механическое значение постоянной вели­чины и, найдем предел скорости v при :

так как при

Следовательно, и - предельная скорость частицы.

Ответ:

и - предельная скорость частицы, и = .

Рис. 10.7, а

10.7. Ускорение рабочего органа вибропитателя, совершающего прямо­линейные колебания, изменяется по закону, характер которого показан на рис. 10.7, а, где Т- период колебаний. Определить законы изменения скоро­сти и координаты рабочего органа, а также найти амплитуду колебаний.

Решение. Вибропитатель совершает прямолинейные ко­лебания, его движение является возвратно-поступательным. Для анализа этого движения достаточно рассмотреть прямолинейные колебания какой-либо одной точки питателя относительно поло­жения равновесия.

Основная ошибка при решении данной задачи обычно состо­ит в том, что полагают скорость в начале периода колебаний = 0. хотя данное утверждение ни на чем не основано. При та­ком выборе начального значения скорость остается положи­тельной весь период Т, а следовательно, перемещение сохраняет одно и то же направление, т. е. движение системы не соответ­ствует заданию.

На первом этапе при ускорение = а = const, движение равноускоренное, поэтому скорость v и координата s

точки (расстояние от данной ее позиции до положения равнове­сия) определяются по формулам (10.18) и (10.17) соответственно:

(1)

(2)

При симметричном цикле колебаний точка проходит поло­жение равновесия в начале, в середине и в конце цикла, т. е.

Подставляя в уравнение (2) значения ,

и получаем

откуда

Теперь при из (1) и (2) имеем

Нa втором этапе при ускорение , движение равнозамедленное. Отсчет времени ведется не от нуля, поэтому скорость v и координату s определим обычным интегрированием, учитывая, что и

Графики изменения скорости и координаты рассмотренной точки рабочего органа вибропитателя показаны соответственно на рис. 10.7 б, в.

Рис. 10.7 б, в

Амплитуда колебаний (наибольшее отклонение точки от положения равновесия) равна наибольшему абсолютному значе­нию расстояния s, которое находим при ds / dt = 0, т. е. при v = 0 и t = T/4:

Ответ: При 0

При

Амплитуда колебаний

10.8. В цикле шагания корпус I экскаватора (рис. 10.8, а) перемещается поступательно по лыжам 2 под действием гидро­цилиндра 3, корпус которого движется относительно поршня с постоянной скоростью и - 0,1 м/с. Составить уравнение движе­ния корпуса и найти его скорость и ускорение, если начальное положение гидроцилиндра определяется размерами l₀ = 2,5 м и h=0,65 м при s = 0, где s - ход поршня. Найти также значения скорости и ускорения в начальный момент движения.

Рис. 10.8, а

Решение. При перемещении экскаватора по лыжам под действием гидроцилиндра нижний шарнир О последнего зани­мает фиксированное положение на задней лыже. Начальное по­ложение А₀ верхнего шарнира А, расположенного на корпусе экскаватора, определяется координатой х₀, при этом расстояние между шарнирами равно l₀ (рис. 10,8, б). При выдвижении штока из корпуса гидроцилиндра шарнир А перемещается горизонтально влево, заставляя корпус экскаватора скользить по лыжам. Промежуточное поло­жение верхнего шарнира А определяется координатой х, а раз­ность координат ∆х = х - х₀ рав­на перемещению корпуса маши­ны. Эту разность найдем из треугольников ОАВ и ОА₀В:

Перемещение корпуса гидроцилиндра относительно штока происходит с постоянной скоростью и, следовательно, ход поршня s = ut, а расстояние между шарнирами А и В

Теперь можно составить уравнение движения корпуса экска­ватора:

Если началом отсчета координаты шарнира А принять точку А₀, то = 0 и уравнение движения принимает вид

Дифференцируя это уравнение по времени и учитывая, что , h и u - постоянные величины, находим скорость скольжения корпуса экскаватора по лыжам:

где

Ускорение корпуса:

В начальный момент движения (при t = 0), когда

Ответ :

Где

В начальный момент 0,104 м/с, - 3 10^-4 м/с².

10.9. В механизме канатной пилы для распиливания камен­ных блоков рабочий орган I (пила) получает возвратно-поступа­тельное движение при оттягивании каната 2 роликом 3, закреп­ленным на ведущем кривошипе 0₁ А (рис. 10.9). Возврат пилы производится пружиной 4. Угол поворота кривошипа изменяет­ся по закону φ=ωt; ω=const. Известны размеры ; Пренебрегая размерами роликов и упругостью каната, определить закон движения и скорость рабочего органа.

У

Рис. 10. 9

Решение. Рабочий ход пилы в рассматриваемом механизме происходит за счет изменения длины участка каната, рас­положенного между блоками О₂ и О₃.

Пренебрегая размерами блоков, из треугольника О₂ А О₃ находим длину каната на этом участке:

Рабочий орган (пила) находится в крайнем левом положении, когда кривошип занимает верхнюю вертикальную позицию 0₁A₀, при этом х_А = 0, у_А = h-r и длина каната на участке между бло­ками О₂ и О₃ минимальна и равна

L₀= .

Канат считаем идеальной нерастяжимой нитью, поэтому ве­личина перемещения s пилы равна изменению длины его изо­гнутого участка между блоками О₂ и О₃.

При повороте кривошипа на некоторый угол φ координаты его пальца А:

х_А = .

Тогда

Раскрывая скобки и обозначая сумму квадратов постоянных величин +h²+r² через р² , получим

Скорость рабочего органа определяем по формуле (10.10):

Ответ:

где р²= +h²+r²;