225

4. Квантововимірні ефекти в напівпровідникових

гетероструктурах

 4. Квантововимірні ефекти

у напівпровідникових гетероструктурах

Якщо просторові розміри системи стають порівнянними з довжиною хвилі де Бройля електрона, електронні властивості системи починають сильно залежати від граничних умов, що вимагають неперервності хвильових функцій та їх похідних на межі розподілу. Ці вимоги є безпосереднім наслідком хвильової природи квантових частинок і є умовами утворення стоячої хвилі в області локалізації частинки. Таким чином, виникнення ефекту квантового конфайнменту (локалізації) залежить як від розмірів області конфайнменту, так і від умов на межах розподілу. Зрозуміло, що такі ефекти повинні спостерігатись у системах, лінійні розміри яких є порівнянними з довжинами хвиль де Бройля. Окрім того, для спостереження квантововимірних ефектів мають виконуватись умови квантової когерентності. Виникає запитання, наскільки реальним є створення систем із розмірами порядку довжини хвилі де Бройля, та чи можливе спостереження таких ефектів. Тобто виникають питання визначення ієрархії параметрів розмірності довжини, що і визначатимуть властивості системи. Таким чином, треба визначити набір електронних фундаментальних довжин та їхні співвідношення між собою та лінійними розмірами системи.

4.1. Електронні фундаментальні довжини

Як видно з попередніх розділів, електрон у напівпровіднику характеризується ефективною масою m^*, яка зазвичай менша за масу вільного електрона. Таким чином, довжина хвилі де Бройля у напівпровіднику є більшою за довжину хвилі де Бройля вільного електрона

. (4.9)

В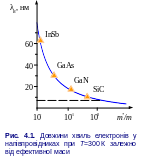 ідомо, що відношення ефективних мас електронів для InSb m^*/m = =0,014, для GaAs m^*/m = 0,067, для GaN m^*/m = 0,172 , для SiC m^*/m = 0,41. Тоді із формули (4.9) маємо абсолютні значення довжин хвиль де Бройля для цих напівпровідників, як це показано на рис. 4.1. Розглянемо тепер, при яких розмірах системи можна очікувати ефекти розмірного (просторового) квантування. Нехай геометричні розміри напівпровідникового зразка є L_xL_yL_z. Припустимо для визначеності, що L_x<L_y<L_z. Якщо розглядувана система є однорідною і процеси розсіювання електронів слабкі, то можна вважати, що рух електронів у такому зразку є квазібалістичним і тільки лінійні розміри системи треба порівнювати з довжиною хвилі де Бройля. Оскільки тільки ціле число напівхвиль де Бройля може вкладатися вздовж будь-якої обмеженої системи, отримаємо, що тільки дискретна кількість електронних станів може існувати в такій системі. Таким чином, рух електрона в обмеженому зразку може бути квантованим. При цьому умови квантування можна визначити ієрархією довжин:

– тривимірний рух електронів можливий у тривимірному об'ємному зразку, де

(4.9)

(у цьому випадку електрон поводить себе як вільна частинка з ефективною масою m^*);

– двовимірна система, або квантова яма – якщо квантування відбувається вздовж однієї з осей (наприклад, Ox), а вздовж інших двох напрямків рух зберігається квазівільним:

; (4.10)

– одновимірна система, або квантовий дріт¹ (квантова нитка – quantum wire) – якщо квантування відбувається вздовж двох напрямків так, що електрон рухається вільно лише вздовж квантового дроту:

; (4.11)

– нуль-вимірна система або квантова точка, якщо квантування відбувається вздовж усіх трьох осей системи:

. (4.12)

Т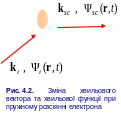 епер візьмемо до уваги, що в реальних системах електрони піддаються процесам розсіяння, що призводить до стохастизації їхнього руху. При цьому, вони перестають поводити себе як квантові об'єкти. Процеси розсіяння поділяються на дві групи – пружні та непружні. При пружному розсіянні з погляду класичної фізики відбувається тільки передача імпульсу, а непружні процеси супроводжуються передачею як імпульсу, так і енергії. Розглянемо як впливають різні типи процесів розсіяння на квантову поведінку електронів. Нехай, наприклад, електрон пружно розсіюється домішкою (рис. 4.2). При цьому, до розсіяння він характеризувався хвильовою функцією із хвильовим вектором . Після розсіяння його хвильовий вектор зміниться і стане рівним , а енергія не зміниться. . Тоді дістанемо, що хвильова функція електрона, яка до розсіяння має вигляд

(4.13)

перейде у хвильову функцію

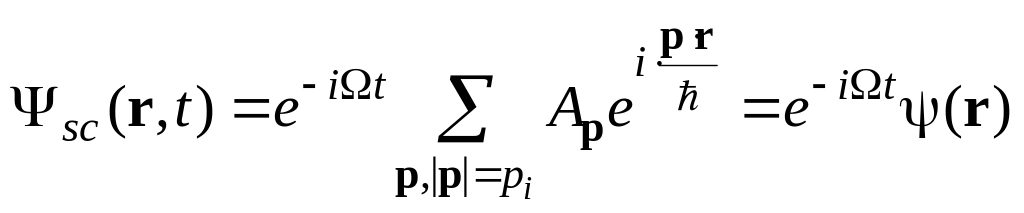. (4.14)

При цьому, як завжди визначає ймовірність знайти частинку з деяким моментом після розсіяння. Падаюча і розсіяна хвилі утворюють комплексну хвильову картину і при пружному розсіянні суттєвою властивістю цієї картини є збереження фази електрона. Це призводить до того, що квадрат модуля хвильової функції (4.14) залишається незалежним від часу:

. (4.15)

Тобто, пружне розсіяння не порушує когерентність електронного руху.

Якщо є середнім часом між двома актами пружного розсіяння, то можна визначити середню довжину пробігу електрона між цими двома актами як

, (4.16)

де – середня швидкість електронів. Таким чином, на відстанях, більших l_e, електрони можна розглядати як когерентні хвильові утворення. У разі, коли електрони розсіюються не пружно (рис. 4.3), замість формули (4.14) запишемо

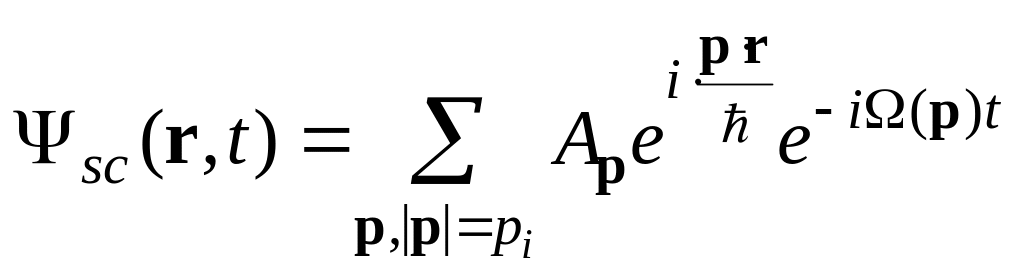. (4.17)

Т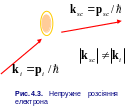 епер квадрат модуля хвильової функції залежить не лише від координати, а й від часу. Тобто, когерентність втрачається. Нехай є середнім часом між двома актами непружного розсіяння, а середня довжина пробігу електрона при непружному розсіянні є L_E . Електрон зберігає квантову когерентність на відстанях менших за L_{E .} Зазвичай L_E набагато перевищує довжину l_e. Тобто, електрон багато разів розсіюється перед тим, як його енергія помітно зменшується (рис. 4.4). Як результат, його рух є хаотичним, і середнє переміщення його за час визначається коефіцієнтом дифузії D:

. (4.18)

Коефіцієнт дифузії може бути виражений формулою

, (4.19)

де параметр  = 3 для тривимірного електронного газу,  = 2 – для двовимірного і  =1 – для одновимірного.

П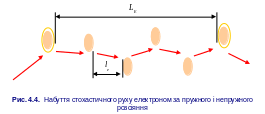 ри збільшенні температури кількість електронів, що можуть брати участь у транспорті, збільшується, і все більша кількість електронів із різною енергією може брати участь у кінетичних процесах. Когерентність у системі при цьому порушується через широкий розподіл фаз хвильових функцій. Дійсно, нехай . Тоді кожен електронний стан має майже однакову амплітуду, але трішки різні фази. Поки ця різниця є малою, усереднення за електронними станами всередині функції розподілу електронів (розмитої за температурою) не порушує їхню фазу і тим самим зберігає когерентність електронів. Але при збільшенні температури, коли електрони з істотно різними енергіями беруть участь у кінетичних процесах, когерентність у системі порушується, оскільки усереднення по станах відбувається із дуже розмитою функцією розподілу електронів. Нехай L_T – характерна довжина, на якій порушується когерентність електронів завдяки ненульовій температурі. Температурне розмиття функції розподілу є пропорційним і призводить до того, що розмиття фаз змінюється з часом як . Таким чином, для оцінки часу розмиття фаз можна використати величину

. (4.20)

Якщо процеси розсіяння є пружними, то електрон дифундує в просторі на відстань порядку за час t , що перевищує середній час вільного пробігу _е . Тобто, протягом часового інтервалу _Т електрон дифундує завдяки термічному рухові на довжину

. (4.21)

Таким чином, когерентність електронів порушується на відстанях, що більші за довжину L_T .

Зрозуміло, що ефекти дефазування, що викликані непружним розсіянням та температурним розмиванням функції розподілу діють одночасно. Тоді просторовий масштаб, пов'язаний із втратою квантово-механічної когерентності, може бути визначеним як менша із двох довжин та

. (4.22)

Оскільки електронний транспорт визначається суперпозицією електронних хвильових функцій, із вищенаведеного розгляду робимо висновок – довжина когерентності l_ визначає такий просторовий розмір, нижче за який електронний транспорт носить квантовий характер.

Можна також розглянути нерівноважну біполярну систему, що містить як електрони, так і дірки. Тоді, якщо _R є часом життя носіїв у системі, то довжина визначатиме середню відстань, на якій нерівноважні носії дифундують перед тим як рекомбінувати.

Таким чином, прилади, в яких геометричні розміри мають порядок довжини когерентності, не можуть описуватись макроскопічними матеріальними параметрами – провідністю, дрейфовою швидкістю і т. д. Такі прилади повинні описуватись квантовою теорією. З іншого боку, прилади із транспортними відстанями L_tr, що є більшими порівняно з довжиною когерентності l_, можуть описуватись поняттями класичної фізики.

Розглянемо тепер умови реалізації квантового та класичного режимів електронного транспорту. Для цього припустимо, що транспорт відбувається вздовж однієї осі. Тобто, повний струм уздовж інших двох осей є нульовим. Але поперечні розміри приладу (уздовж цих осей) можуть відігравати важливу роль. Можна визначити декілька принципово різних типів транспорту електронів у просторово обмежених системах. Почнемо з квантового режиму та мезорежиму транспорту. Якщо довжина хвилі де Бройля перевищує лінійні розміри приладу L_z:

, (4.23)

і окрім цього виконується нерівність

l_e>>_B, (4.24)

то маємо квантово-балістичний режим електронного транспорту. Випадок, коли

l_ > L_z, _B (4.25)

відповідає мезорежиму електронного транспорту. Таким чином, можна стверджувати, що поперечні (до осі Оz) розміри приладу визначають одно-, дво-, та тривимірний характери квантово-балістичного режиму та мезорежиму електронного транспорту.

Класичний режим електронного транспорту реалізується у випадку, коли виконується нерівність

L_z > l_. (4.26)

Якщо лінійний розмір приладу вздовж осі Oz при цьому є меншим за довжину вільного пробігу електрона, то відбувається класичний балістичний режим електронного транспорту. Іншими словами, у цьому випадку електрони можуть рухатись уздовж приладу по класичних траєкторіях без зіткнень. Якщо

L_z >> l_, (4.27)

то електронний транспорт має дифузійну природу. У випадку, коли виконуються співвідношення

L_z ~ l_E >> l_e, (4.28)

електрони не втрачають енергію, рухаючись уздовж приладу. Тоді вважають, що реалізується квазібалістичний режим електронного транспорту. Зрозуміло, що можуть реалізуватись три класичні режими електронного транспорту для одно-, дво- та тривимірних рухів електронів. Якщо обидва поперечні розміри приладу L_x та L_y значно більші за довжину хвилі де Бройля, але порівнянні з характеристичними класичними довжинами, будуть спостерігатися поперечні класичні розмірні ефекти в електронному транспорті. У цьому випадку зіткнення електронів із поперечними поверхнями приладу будуть визначати транспорт уздовж осі Oz. Наприклад, якщо один із двох поперечних розмірів приладу має порядок довжини вільного пробігу електронів , то опір приладу вздовж осі Oz залежатиме від його бічних меж. Якщо поперечні розміри приладу стають порівнянними з однією з дифузійних довжин, ми отримаємо інший тип класичних розмірних ефектів. Наприклад, якщо L_x або L_y мають порядок довжини релаксації енергії L_Е межі приладу забезпечують додатковий канал релаксації енергії. Такий дифузійно-розмірний ефект визначає середню енергію нерівноважних електронів.

 4.2. Гетероструктури. Квантові ями,

квантові голки, квантові точки

Гетероструктура формується, коли два різних матеріали з'єднуються в одну структуру із межею розподілу між ними. Умови формування гетероструктур і різні типи гетерограниць ми розглядали в розділі 1. У цьому підрозділі скористаємось відомими матеріалами і розглядатимемо гетероструктури, у яких може спостерігатись просторове квантування. Найпростішими і найпоширенішими такими гетероструктурами є квантові ями. Розглянемо властивості квантових ям, а також квазіодновимірних об'єктів – квантових голок, та квазінульвимірних – квантових точок.

Сучасні технології дозволяють ці межі розподілу виготовляти майже ідеальними. Так, перехідний шар, що утворюється на межі розподілу завдяки досягненням сучасних технологій, що базуються на методі молекулярно-променевої епітаксії, може бути доведеним до моноатомного. Найпростішим прикладом гетероструктури є два напівпровідникові матеріали з однією межею розподілу (гетероконтактом). Відомими прикладами гетероструктур є SiO₂-Si гетероз'єднання з дуже малою щільністю дефектів на інтерфейсі. Можна вказати на такі широковживані пари III-V напівпровідників, що утворюють промислові гетероструктури: GaAs-AlGaAs; GaInAs-InP; GaInAs-AlInAs; GaSb-AlSb; GaN-AlN і т. д. Іншим прикладом гетероструктур є структури сполук II-VI: CdZnSe-ZnSe; ZnSTeSe-ZnSSe і т. д.

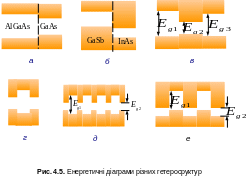
Головною метою при отриманні гетероструктур є контрольована модифікація енергетичних зон носіїв у цих структурах. Інакше кажучи, гетеросруктури можна розглядати як штучні речовини з наперед заданими властивостями. На рис. 4.5 показано зонні діаграми для деяких напівпровідникових гетероструктур: на (а) та (б) зображено два типи гетероструктур з однією межею розподілу, на (в) та (г) – різні типи гетероструктур із двома межами розподілу, на (д), (е) подано багатоінтерфейсні гетероструктури. Нижче розглянемо ідеалізовану картину трьох типів квантових структур – квантові ями, дроти та точки.

 4.3. Квантові ями

К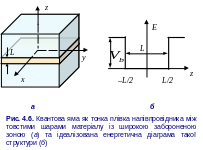 вантова яма може утворитись, коли тонкий шар з одного матеріалу вирощується між двома іншими шарами з різних матеріалів, які характеризуються ширшою забороненою зоною, ніж матеріал центрального шару (рис. 4.6). Розривність зон при цьому призводить до обмеженості руху (конфайнменту) носіїв усередині ями. Тобто, рух електрона тепер відбуватиметься у обмежуючому потенціалі. Для більшості випадків квантових ям такий потенціал вважатимемо прямокутним. Розглянемо ідеалізований потенціал, як це показано на рис. 4.6:

(4.29)

де V_b та L є глибина та ширина ями відповідно. Оскільки потенціал залежить тільки від однієї змінної, ми можемо застосувати метод змінних, що розділяються. Тобто, рух електронів у площині xOy буде вільним, і тоді хвильову функцію можна зобразити у вигляді

. (4.30)

Після підстановки цієї хвильової функції у рівняння Шредингера

, (4.31)

отримаємо таке рівняння для невідомої функції (x):

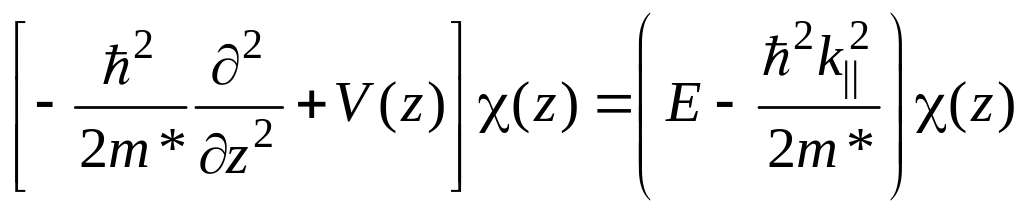. (4.32)

Тут , а є кінетичною енергією руху електрона з ефективною масою у площині xOy. Уведемо позначення

. (4.33)

Оскільки Е є повною енергією частинки, то буде енергією руху частинки в напрямку, нормальному до площини хOу, тобто поперечного руху. Таким чином, ми відокремили змінні – поперечну (z) від площинних (x,y) і тим самим звели проблему до одновимірної

. (4.34)