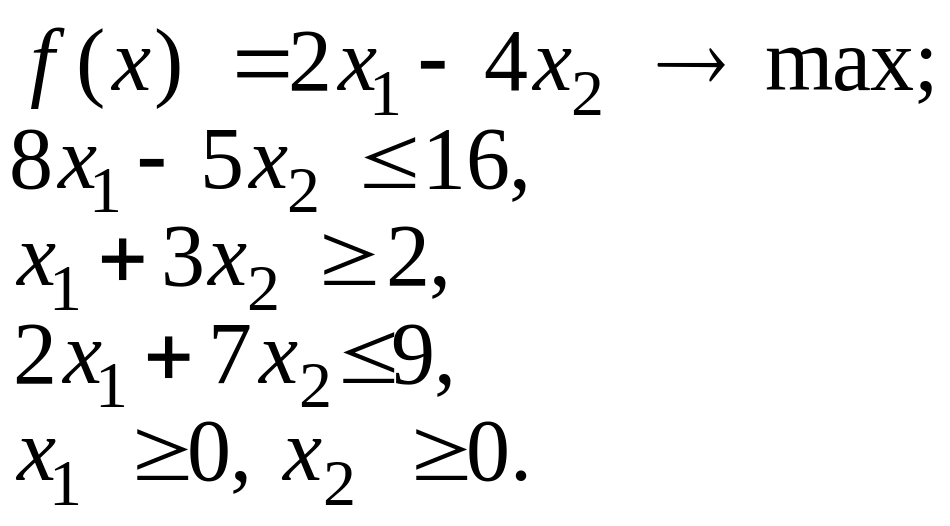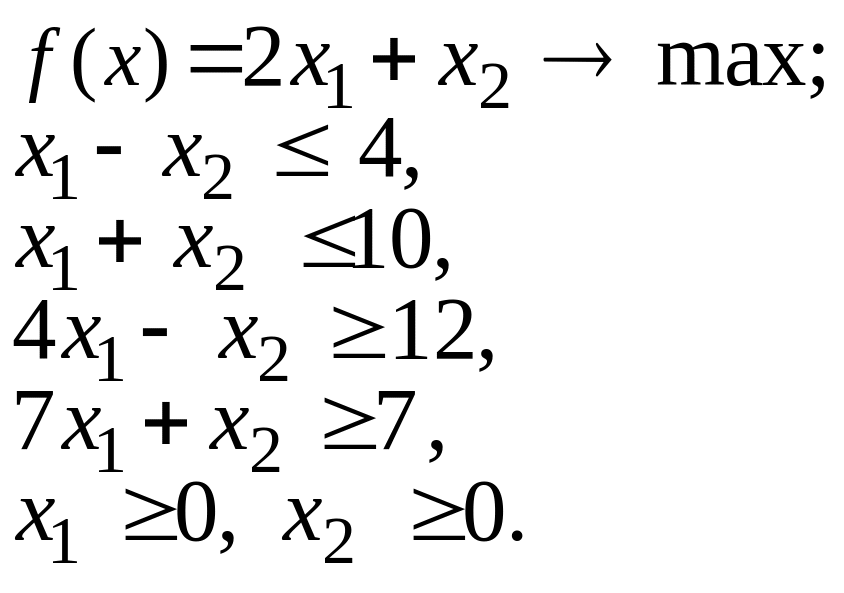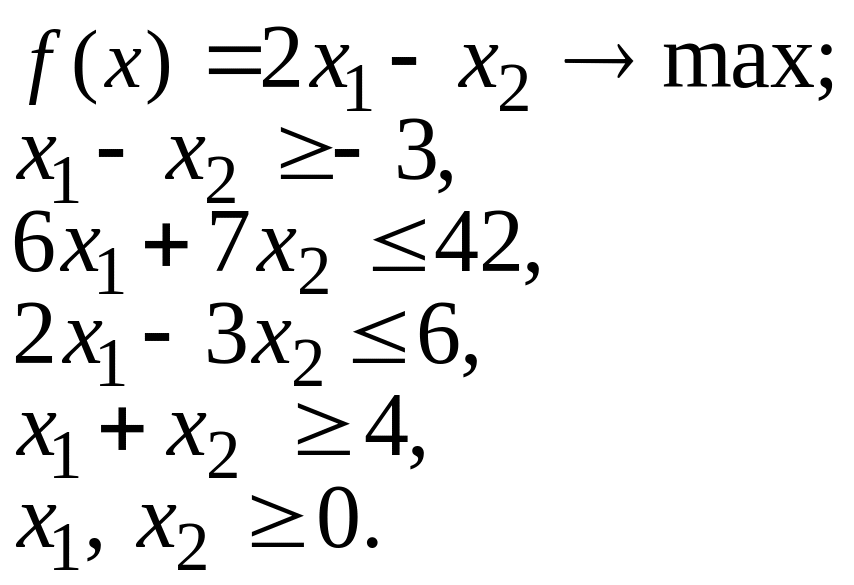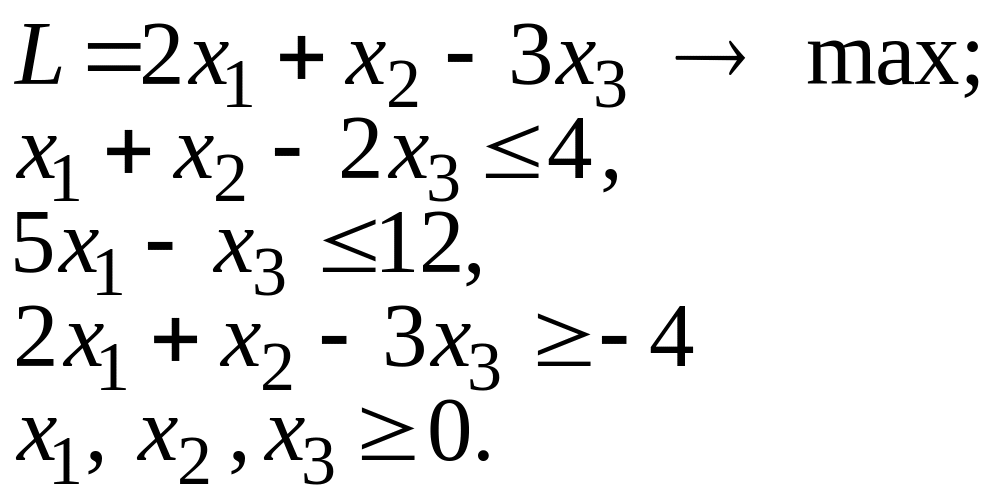ЛАБОРАТОРНІ РОБОТИ 1-6

з дисципліни

"Математичні методи дослідження операцій"

ЛАБОРАТОРНА РОБОТА № 1

ТЕМА: Графічний метод розв’язування задач лінійного програмування (ЛП).

МЕТА: Опанувати графічний метод побудови допустимої області ЗЛП та ліній рівня цільової функції; засвоїти зв'язок між екстремальними точками цільової функції та кутовими точками многокутника; встановити зв'язок між лініями рівня цільової функції та її антиградієнтом.

КОНТРОЛЬНІ ЗАПИТАННЯ

Дати короткі теоретичні відомості, в яких відобразити наступні питання:

1. Поняття випуклої множини.

2. Поняття многокутника, випуклої лінійної комбінації точок та крайніх (кутових) точок фігури.

3. Многокутник, як випукла комбінація вершин. Кутові точки, як точки можливого екстремуму лінійної функції.

4. Взаємозв'язок між паралельним переносом лінії рівня цільової функції та її антиградієнтом.

5. Виділити випадок необмеженої допустимої області ЗЛП.

6. Можливість альтернативного розв'язку та відсутність розв'язку в ЗЛП.

7. Зведення задач ЛП вищої розмірності до плоского випадку.

Завдання

1. Розв’язати задачі лінійного програмування графічним методом.

1.1.		1.2.
1.3.		1.4.
1.5.		1.6 .
1.7.		1.8 .
1.9.		1.10.

2. Задачі лінійного програмування в канонічному вигляді розв’язати графічним методом.

2.1.		2.2.
2.3.		2.4.
2.5.		2.6 .
2.7.		2.8 .
2.9.		2.10.

Номер варіанта обирається згідно останньої цифри залікової книжки!

Звіт про виконання лабораторної роботи повинен містити:

• формулювання задачі;

• хід розв’язку;

• отримані чисельні результати;

• аналіз результатів;

• висновки.

Лабораторна робота № 2

ТЕМА: Симплекс-метод розв’язування задач лінійного програмування (ЛП).

МЕТА: Опанувати симплекс-метод розв’язування задач лінійного програмування

користуючись програмою Microsoft Excel.

Контрольні запитання

Дати короткі теоретичні відомості, в яких відобразити наступні питання:

1. Поняття опорного (базисного) плану кутової точки багатогранника.

2. Поняття оптимального плану задачі ЛП, та його ідентифікація у симплекс-таблиці.

3. Алгоритм знаходження опорного плану методом відбору.

4. Алгоритм знаходження опорного плану методом штучних змінних.

5. Алгоритм знаходження оптимального плану.

6. Випадок виродження системи обмежень.

7. Випадок, коли лінійна форма не обмежена.

Завдання

1. Розв’язати задачі лінійного програмування симплекс-методом

1.1.		1.2.
1.3.		1.4.
1.5.		1.6 .
7.		1.8 .
1.9.		1.10.

2. Задачі лінійного програмування розв’язати симплекс-методом

2.1.

2.2.

Параметр дорівнює , де .

Номер варіанта обирається згідно останньої цифри залікової книжки!

Звіт про виконання лабораторної роботи повинен містити:

• формулювання задачі;

• хід розв’язку;

• отримані чисельні результати;

• аналіз результатів;

• висновки.

Лабораторна робота № 3

ТЕМА: Транспортна задача.

МЕТА: Засвоїти метод потенціалів розв’язування транспортної задачі.

Контрольні запитання

Дати короткі теоретичні відомості, в яких відобразити наступні питання:

1. Дати економічну і математичну постановку транспортної задачі.

2. Чим відрізняється транспортна задача від загальної задачі лінійного програмування?

3. Властивості опорних планів транспортної задачі.

4. Чим відрізняється відкрита транспортна задача від закритої ?

5. Як перетворити відкриту транспортну задачу на закриту ?

6. Метод лінійного елементу побудови опорного плану.

7. Знаходження потенціалів та умови оптимальності.

8. Алгоритм методу потенціалів розв’язання транспортної задачі.

9. Випадок вродженості опорного плану.