
- •Тема 1. Елементи теорії матриць та визначників
- •Тема 2. Загальна теорія систем лінійних рівнянь
- •Тема 3. Лінії на площині
- •Тема 4. Елементи аналітичної геометрії на площині та у просторі
- •Тема 5. Криві другого порядку
- •Тема 6. Границі функції
- •Тема7. Неперервність функції
- •Тема 8. Похідна функції
- •Тема 9. Диференціал функції однієї змінної
- •Тема 10. Основні теореми диференціального числення
- •Тема 12. Дослідження функції багатьох змінних на екстремум, умовний екстремум
- •Тема 13. Невизначений інтеграл
- •Тема 14. Визначений інтеграл
- •Тема 15. Диференціальні рівняння першого порядку
- •Тема 16. Числові ряди, їх збіжність
- •Тема 17. Степеневі ряди
Тема 15. Диференціальні рівняння першого порядку
Основні означення. Диференціальні рівняння першого порядку. Задача Коші. Теорема існування та єдності розв`язку. Економічні задачі, що потребують використання диференціальніих рівнянь.
Диференціальні рівняння з відокремленими та відокремлюваними змінними.
Однорідні рівняння першого порядку.
Лінійні диференціальні рівняння першого порядку, рівняння Бернулі.
Розділ 7. РЯДИ
Тема 16. Числові ряди, їх збіжність
Ряди. Основні означення. Збіжність рядів. Властивості збіжних рядів. Гармонічний ряд. Необхідна умова збіжності. Ряд геометричної прогресії.
Ряди з додатними членами. Достатні ознаки збіжності рядів з додатними членами: ознака порівняння, ознака Д`аламбера, ознаки Коші (радикальна й інтегральна).
Знакозмінні ряди. Абсолютна та умовна збіжність. Теореми Лейбніца та Коші.
Тема 17. Степеневі ряди
Степеневі ряди. Теорема Абеля. Радіус збіжності. Область збіжності степеневого ряду. Розкладення функції в степеневий ряд. Застосування степеневих рядів до наближених обчислень. Диференціювання та інтегрування степеневих рядів.
Ряди Тейлора, Маклорена. Розклад елементарних функцій в ряд Тейлора.
ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ
НА ІСПИТ
Форма проведення атестації - іспит. Кожен білет складається з трьох питань (2 теоретичних та 1 практичний). Час на підготовку 40 хвилин.
Оцінка за відповідь виставляється за чотирьохбальною системою: «відмінно», «добре», «задовільно», «незадовільно» як середньоарифметична з 2-х оцінок: за теоретичну та практичну частину.
Лінійна алгебра
Числові матриці: означення, розміри, типи. Множення матриць на число, додавання матриць. Транспонування. Властивості цих дій.
Числові матриці. Множення матриць. Властивості множення.
Визначники: означення, властивості. Обчислення визначників 2-го , 3-го і n-го порядку. Теорема Лапласа.
Обернена матриця: означення, існування, єдиність, алгоритм побудови.
Ранг матриці. Методи обчислення рангу матриці. Теореми про ранг матриці.
Системи лінійних алгебраїчних рівнянь. Формули Крамера та метод Гаусса для розв’язування систем.
Теорема Кронекера-Капеллі.
Дослідження систем лінійних алгебраїчних рівнянь.
Системи лінійних алгебраїчних рівнянь. Матричний метод розв’язування систем рівнянь
Аналітична геометрія
Поняття вектора. Лінійні операції над векторами: сума векторів, добуток вектора на число, скалярний добуток векторів.
Розклад вектора в ортонормованому базисі. Операції над векторами, заданими в координатній формі.
Лінійна залежність векторів. Розклад вектора за базисом.
Скалярний, векторний, мішаний добутки векторів: означення, властивості. Кут між двома векторами.
Рівняння прямої на площині: загальне, з кутовим коефіцієнтом, що проходить через дві задані точки. Взаємне розташування прямих.
Рівняння прямої, що проходить через дві задані точки у просторі. Умови паралельності і перпендикулярності прямої і площини.
Загальне рівняння площини. Дослідження загального рівняння площини.
Поняття про рівняння площини і прямої у просторі. Умова паралельності і перпендикулярності двох площин.
Рівняння площини, що проходять через три задані точки. Кут між двома площинами.
Нормальне рівняння площини. Відстань від точки до площини.
Кут між прямими. Умови перпендикулярності і паралельності двох прямих.
Загальне рівняння лінії другого порядку на площині. Коло.
Еліпс: означення, властивості, канонічне рівняння.
Гіпербола: означення, властивості, канонічне рівняння.
Парабола: означення, властивості, канонічне рівняння.
Диференціальне числення
Границі функції в точці: означення, умови існування, основні теореми про границі функції. Визначальні границі.
Означення границі функції. Односторонні границі. Теореми про нескінченно малі та нескінченно великі функції.
Неперервність функції в точці. Класифікація точок розриву.
Неперервність функцій в точці. Теореми про неперервність функцій на відрізку.
Похідна функції: означення, геометричний та економічний зміст. Правила диференціювання.
Похідна функції. Необхідна умова існування похідної функції в точці. Правила диференціювання.
Похідна складеної та оберненої функції. Диференціювання функцій, заданих в неявному вигляді.
Похідна функції, заданої в неявному вигляді. Похідна степенево-показникової функції.
Похідна по напрямку. Градієнт.
Основні теореми диференціального числення: теореми Ферма, теорема Ролля, теорема Лагранжа.
Правило Лопіталля.
Диференціал функції однієї змінної. Правила обчислення диференціалу до наближених обчислень.
Умова монотонності функції однієї змінної. Достатні умови зростання, спадання функції.
Екстремум функції однієї змінної. Необхідна і достатня умова екстремуму функції однієї змінної.
Асимптоти графіка функції.
Загальна схема дослідження функцій однієї змінної методами диференціального числення та побудова графіків.
Напрямки опуклості графіка функції. Точки перегину.
Функції багатьох змінних: означення, область визначення, область значень.
Повний диференціал функцій двох змінних, правило його знаходження та застосування в наближених обчисленнях.
Екстремум функції багатьох змінних: означення, необхідна і достатня умова екстремуму функцій двох змінних.
Умовний екстремум функцій двох змінних. Метод множників Лагранжа.
Інтегральне числення
Невизначений інтеграл. Властивості первісної та невизначеного інтеграла. Таблиця основних інтегралів.
Безпосереднє інтегрування. Заміна змінної в невизначеному інтегралі. Таблиця основних інтегралів.
Інтегрування різних типів невизначених інтегралів частинами.
Інтегрування раціональних дробів. Метод невизначених коефіцієнтів.
Інтегрування деяких видів ірраціональностей.
Інтегрування тригонометричних функцій.
Визначений інтеграл: інтегральні суми, означення, властивості.
Визначений інтеграл. Формула Ньютона-Лейбніца.
Заміна змінної і формула інтегрування частинами у визначеному інтегралі.
Геометричне застосування визначеного інтегралу: обчислення площ плоских фігур, об`ємів тіл обертання.
Геометричне застосування визначеного інтегралу: обчислення довжини дуги кривої, площі поверхні обертання.
Невласні інтеграли: інтеграли з нескінченними межами інтегрування.
Наближені методи обчислення визначених інтегралів: формули прямокутника, трапеції, Сімпсона.
Подвійні, потрійні інтеграли. Зведення подвійного інтеграла до повторного.
Перелік практичних завдань
ЛІНІЙНА АЛГЕБРА
1.Розв`язати систему лінійних рівнянь методом Гаусса.
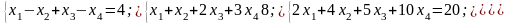
2.Знайти значення виразу f(x)=3x2-2x+5, якщо

3.При якому значенні а визначник дорівнює 0?

4.Доведіть що система має безлічь розв`язків.

5.Знайти для матриці А обернену.

6.Обчислити АВ, (СТВТ), якщо

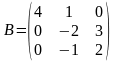 ,
,
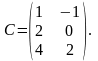
7.Чи має матриця А обернену?
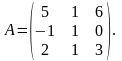
8.При якому значенні а система не має розв`язків?
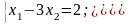
9.Розв`язати систему лінійних рівнянь за формулами Крамера.

10.Обчислити ВС, (ВС)Т, якщо
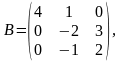
11.При якому значенні а визначник дорівнює 0?

12.При якому значенні а система не має розв`язків?

АНАЛІТИЧНА ГЕОМЕТРІЯ
1.Дано вершини трикутника А(-1; -1), В(0; 6), С(-10; -2). Записати рівняння сторони ВС і знайти довжину медіани, проведеної з вершини А.
2.Дано гіперболу 16x2 – 25y2 = 400. Знайти: 1) його напіввісі; 2) фокуси; 3) ексцентриситет.
3.Записати рівняння прямої, яка проходить через точку М(-2; 7; 3) паралельно площині
x – 4y + 5z + 1 = 0.
4.Дано еліпс 16x2 + 25y2 = 400. Знайти: 1) його напіввісі; 2) фокуси; 3) ексцентриситет.
5.Скласти рівняння еліпса, що проходить через точки А(2 2; 6 ) і В(6; 0).
6.Знайти площу трикутника АВС, якщо А(1; 1; 1), В(-2; -1; 0), С(3; -2; 2).
7.Скласти рівняння площини, що проходить через точку А(3; 5; -7) і відтинає на координатних осях однакові відрізки.
8.Скласти рівняння кола, для якого відрізок АВ є діаметром. Якщо А(1; 5), В(0; 4).
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
З
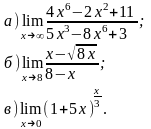 найти
границю функції.
найти
границю функції.Обчислити наближено.
З
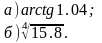
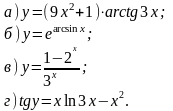 найти
похідні функцій.
найти
похідні функцій.
4 .Знайти
границю функції.
.Знайти
границю функції.
5 .Обчислити
наближено.
.Обчислити
наближено.
6.Знайти похідні функцій.
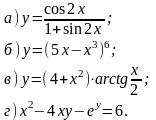
ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
О
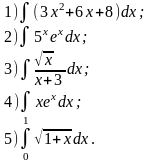 бчислити
інтеграли.
бчислити
інтеграли.
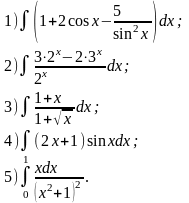
Знайти площу фігури обмеженої лініями

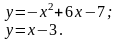
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ. РЯДИ
Знайти загальний розв`язок диференціального рівняння та частинний розв`язок, який задовольняє початковій умові
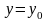 при
при
 .
.
A)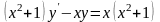 ,
,
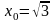 ,
, .
.
б)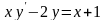 ,
,
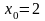 ,
,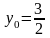 .
.
В)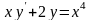 ,
,
 ,
,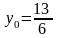 .
.
Г) ,
,
.
,
,
.
Дослідити на збіжність ряди:
а)
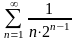 ;
б)
;
б)
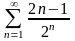 ;
в)
;
в)
 .
.
г)
 ;
д)
;
д)
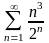 ;
е)
;
е)
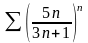 .
.
ж)
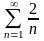 ;
з)
;
з)
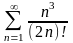 ;
и)
;
и)
 .
.
к)
 ;
л)
;
л)
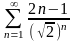 ;
м)
;
м)
 .
.
3. Дослідити на збіжність знакозмінні ряди. Якщо ряд збіжний, то визначити збігається він абсолютно чи умовно.
а)
 ;
б)
;
б)
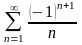 .
.
.
в)
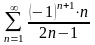 ;
г)
,
;
г)
,
д)
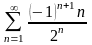 ;
е)
;
е)
 .
.
ж)
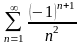 ;
з)
;
з)
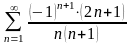 .
.
Диференціальні рівняння
Диференціальні рівняння: його порядок, частинний та загальний розв`язок. Задача Коші.
Неповні диференціальні рівняння першого порядку. Диференціальні рівняння з відокремлювальними змінними.
Однорідні диференціальні рівняння першого порядку.
Лінійні диференціальні рівняння першого порядку. Рівняння Бернулі. Загальний та частинний розв`язок.
Ряди
Числові ряди: означення, властивості, необхідна ознака збіжності. Гармонічний ряд. Ряд геометричної прогресії.
Достатні умови збіжності числових рядів з додатними членами.
Ряди з членами довільного знаку. Ознака Лейбніца. Достатня умова збіжності знакозмінного ряду. Абсолютна та умовна збіжноті ряду.
Степеневі ряди: структура області збіжності, основні властивості. Теорема Абеля.
Ряди Тейлора і Макларена.
