Расчетно-графическая работа №119

Министерство Образования и науки Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра теоретических основ электротехники

Расчетно-графическая работа №1

Анализ цепей постоянного тока

Выполнил студент группы АТП-236:

Лазуков Никита

Проверил:

Грахов П.А.

УФА 2007

2

I₄

E₅

I₅

R₄

R₅

R₆

I₃

1

3

R₃

I₁

I₂

j

R₁

_k1

E₂

I₆

R₂

4

Исходные данные:

R₁ = 10 Ом E₁= 0 B J_K1= 8 A

R₂ = 80 Ом E₂= 450 B J_K2= 0 A

R₃ = 60 Ом E₃=00 B J_K3= 0 A

R₄ = 40 Ом E₄= 0 B

R₅ = 30 Ом E₅= -200 B

R₆ = 20 Ом E₆= 0 B

1. Расчет цепи методом контурных токов

Составим уравнения по второму закону Кирхгофа:

I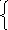₁₁(R₁+R₂+R₃) – I₂₂R₃ -I₃₃R₂ –jR₁ = -E₂

–I₁₁R₃ + I₂₂(R₃+R₄+R₅) - I₃₃R₅-jR₄ = -E₅

-I₁₁R₂ - I₂₂R₅ + I₃₃(R₂+R₅+R₆) = E₂+E₅

Решая систему уравнений находим:

I₁₁=1217/406=2.997 А I₂₂= 5363/812 А=6.604 А I₃₃=4297/812 А= 5.292 А

Находим Реальные токи в ветвях:

I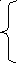₁=I₁₁ -j= -5,003 А

I₂= I₃₃- I₁₁=2.295 А

I₃= -I₁₁+ I₂₂=3.607 А

I₄= I₂₂ -j=-1.396 А

I₅= -I₂₂+I₃₃=-1,312 А

I₆=I₃₃=5.292 А

2. Расчет цепи методом узловых потенциалов

I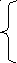₁=( φ₄ – φ₁)/R₁=– φ₁/R₁

I₂=( φ₄ – φ₃+E₂)/R₂=(– φ₃+E₂)/R₂

I₃=( φ₃ – φ₁)/R₃

I₄=( φ₁ – φ₂)/R₄

I₅=( φ₃ – φ₂+Е₅)/R₅

I₆=( φ₂ – φ₄)/R₆= φ₄/R₆

I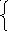₁+ I₃- I₄=0

I₄+ I₅-I₆+j=0

I₂-I₃-I₅=0

Составим систему уравнений, используя две предыдущие системы:

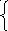– φ₁/R₁+( φ₃ – φ₁)/R₃-( φ₁ – φ₂)/R₄=0

( φ₁ – φ₂)/R₄+( φ₃ – φ₂+Е₅)/R₅-φ₂/R₆+j=0

(– φ₃+E₂₎/R₂-( φ₃ – φ₁)/R₃-( φ₃ – φ₂+Е₅)/R₅=0

Решая систему находим потенциалы φ₁, φ₂, φ₃:

φ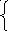₁=10155/203 В=50,025 В

φ₂=21485/203 В=-105,837 В

φ₃=54090/203 В=266,453 В

Находим токи:

I₁= 2031/406 А= -5,003 А

I₂=1863/812 А=2,295 А

I₃= 101/28 А=3,607 А

I₄= -1133/812 А= -1,396 А

I₅= -533/406 А=-1,312 А

I₆= 4297/812 А=5,292 А

3. Проверка по законам Кирхгофа

Проверка по первому закону Кирхгофа:

I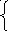₁+ I₃- I₄=0

I₄+ I₅-I₆+j=0

I₂-I₃-I₅=0

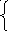-2031/406 +101/28+1133/812=0

-1133/812-533/406-4297/812+8=0

1863/812-101/28+533/406=0

Первый закон Кирхгофа выполняется

Проверка по второму закону Кирхгофа:

I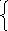₃ R₃ + I₄ R₄ – I₅ R₅ = – E₅

I₁ R₁ – I₃ R₃ – I₂ R₂ = -E₂

I₅ R₅ + I₆ R₆ + I₂ R₂ = E₅ + E₂

101*60/28-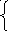1133*40/812+533*30/406 =200

2031*10/406 -101*60/28-1863*80/812=-450

-533*30/406+4297*20/812 +1863*80/812 =-200+450

Второй закон Кирхгофа выполняется

4. Баланс мощностей

E₅I₅ + E₅I₂ + j U_J= I₁²R₁ + I₂²R₂ + I₃²R₃ + I₄²R₄ + I₅²R₅ + I₆²R₆

2141,711823=2141,711823

Баланс мощностей соблюдается.

5. Определение тока I₁ методом эквивалентного генератора

Рассчитаем сопротивление цепи:

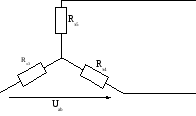
R_э1=(R₄ * R₅)/(R₃ + R₄ + R₅)

R_э2=(R₃ * R₅)/(R₃ + R₄ + R₅)

R_э3=(R₃ * R₄)/(R₃ + R₄ + R₅)

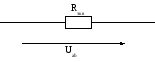
R_э4 = R₂ + R_э2

R_э5 = R₆ + R_э1

R_экв=(R_э4 * R_э5)/(R_э4 + R_э5) + R_э3

R_э1=9,230 Ом

R_э2=13,846 Ом

R_э3=18,461 Ом

R_э4 =93,846 Ом

R_э5 =29,230 Ом

R_экв=40,75 Ом

Определим потенциалы узлов в отсутствии ветви с сопротивлением R₁

I₃- I₄=0

I₄+ I₅-I₆+j=0

I₂-I₃-I₅=0

Составим систему уравнений, используя две предыдущие системы:

( φ₃ – φ₁)/R₃-( φ₁ – φ₂)/R₄=0

( φ₁ – φ₂)/R₄+( φ₃ – φ₂+Е₅)/R₅-φ₂/R₆=0

(– φ₃+E₅)/R₂-( φ₃ – φ₁)/R₃-( φ₃ – φ₂+Е₅)/R₅=0

Решая систему находим потенциалы φ₁, φ₂, φ₃:

φ₁=2031/8 В=253,875В

φ₂=1457/8 В

φ₃= 723/2 В

U_ab= φ₄ -φ₁=253,875 B I₁= U_ab/(R_экв+R₁) I₁=-2031/406=-5,003 A

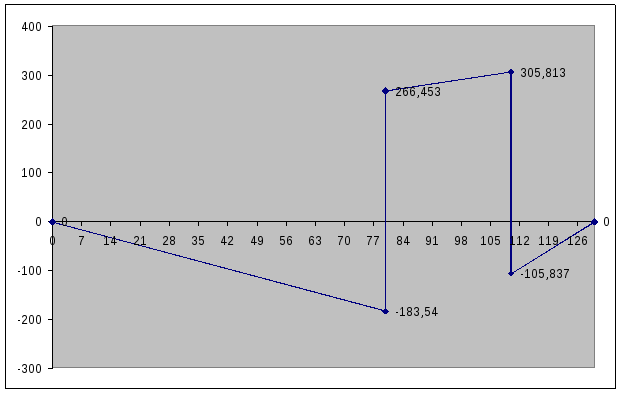
6. Потенциальная диаграмма

φ₄=0 В φ₅= φ₄-I₂R₂=-183,54 B φ₃=266,453 B φ₆= φ₃- I₅R₅=305,813 B

φ₂=-105,837 В