
Расчетно-графическая работа №11
.rtfЗадание:
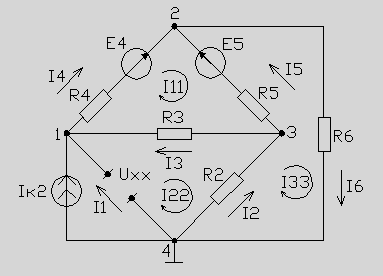
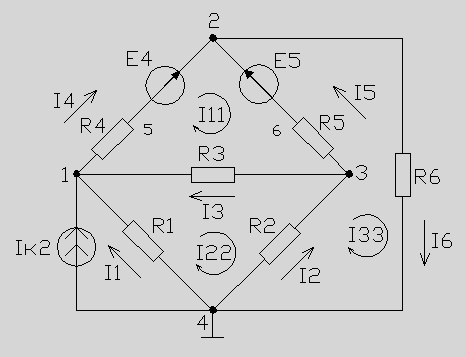
1. Определить токи во всех ветвях методом контурных токов.
2. Определить токи во всех ветвях методом узловых напряжений, приняв потенциал четвертого узла равным нулю.
3. Произвести проверку по законам Кирхгофа.
4. Составить баланс мощностей.
5. Определить ток I1 методом эквивалентного генератора.
6. Начертить в масштабе потенциальную диаграмму для любого контура, включающего в себя две ЭДС.
Исходные данные:
R1=10 Ом E1=0 Ik1=0
R2=80 Ом E2=0 Ik2=9 А
R3=50 Ом E3=0 Ik3=0
R4=30 Ом E4=-200 В
R5=10 Ом E5=250 В
R6=10 Ом E6=0

1. Расчет цепи методом контурных токов
Определяем количество необходимых уравнений: nII=В-Вi-(У-1)=7-1-(4-1)=3
Введем контурные токи I11, I22, I33 и запишем уравнения по методу контурных токов:
I11R11 + I22R12 + I33R13 = E11
I11R21 + I22R22 + I33R23 = E22
I11R31 + I22R32 + I33R33 = E33
Определим собственные и взаимные сопротивления:
R11=R3+R4+R5=50+30+10=90 Ом
R22=R1+R2+R3=10+80+50=140 Ом
R33=R2+R5+R6=80+10+10=100 Ом
R12=R21=-R3=-50 Oм R13=R31=-R5=-10 Oм R32=R23=-R2=-80 Oм
Определим собственные ЭДС:
E11= Е4-Е5=-450 В E22=Jк2•R1=90 В E33= Е5=250 В
Составим матрицу и найдем контурные токи, используя программу Gauss:

I11≈ -4,553 A; I22≈ 0,341 A; I33≈ 2,318 A.
Найдем реальные токи I1, I2, …, I6:
I1= -Iк2 + I22=-9 + 0,341≈8,659 А
I2= -I22 + I33=-0,341 +2,318≈1,977 А
I3= -I22 + I11=-0,341 + (-4,553)≈-4,894 А
I4= I11= -4,553 А
I5= -I11 + I33=4,553 + 2,318 = 6,871 А
I6= I33 =2,318 А
2. Расчет цепи методом узловых потенциалов
Определим число уравнений и запишем их:
nуз=У-1=4-1=3
G11φ1 + G12φ2 + G13φ3 = J11
G21φ1 + G22φ2 + G23φ3 = J22
G31φ1 + G32φ2 + G33φ3 = J33
Используя обобщенный закон Ома, определим токи во всех ветвях:
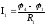 ;
;
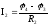 ;
;
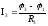 ;
;
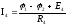 ;
;
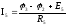 ;
;
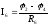
Определим собственные и взаимные проводимости:


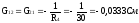
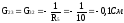
Определим токи:
J11 = Jк2 – E4/R4 =9 – (-200)/30=15,6667 A
J22= E4/R4 + E5/R5 =(-200)/30 + 250/10=18,3333 A
J33 = -E5/R5=-250/10=-25 A
Составим матрицу и, используя программу Gauss, определим потенциалы точек:

φ1=86,5992 В φ2=23,1662 В φ3=-158,1237 В φ4=0 B
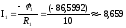 А
А
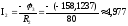 А
А
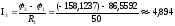 А
А
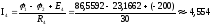 А
А
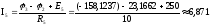 А
А
 А
А
Таблица токов
|
Токи |
I1, A |
I2, A |
I3, A |
I4, A |
I5, A |
I6, A |
|
по методу контурных токов |
-8,659 |
1,977 |
-4,894 |
-4,553 |
6,871 |
2,318 |
|
по методу узловых потенциалов |
-8,659 |
1,977 |
-4,894 |
-4,554 |
6,871 |
2,317 |
3.Проверка по законам Кирхгофа
По первому закону Кирхгофа:
для
1 узла:
I1+Iк2+I3-I4=0
-8,659+9-4,894-(-4,553) 0
0
для
2 узла:
I4+I5-I6=0
-4,553+6,871-2,318 0
0
для
3 узла:
I2-I3-I5=0
1,977-(-4,894)-6,871 0
0
По второму закону Кирхгофа:
1 контур: I2R2+I5R5+I6R6=Е5 1,977*80+6,871*10+2,318*10≈250 (выполняется)
2 контур: I1R1-I3R3-I2R2=0 (-8,659)*10-(-4,894)*50-1,977*80≈0 (выполняется)
3 контур: I3R3+I4R4-I5R5= E4-Е5 (-4,894)*50+(-4,553)*30-6,871*10≈-200-250 (вып-ся)
Законы Кирхгофа выполняются, значит, токи найдены правильно.
4. Баланс мощности.
Рнагр =I12R1+I22R2+I32R3+I42R4+I52R5+I62R6
Рнагр
=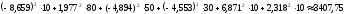 Вт
Вт
Рист
=E3I3+E6I6+Ik3(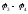 )
)
Рист=
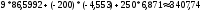
 Вт
Вт
Баланс мощности соблюдается.
5. Расчет тока I1 методом эквивалентного генератора.
Определим Uxx (при отсутствии нагрузки R1), используя метод узловых потенциалов.
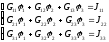
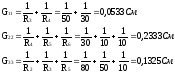
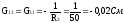
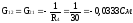
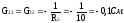
Определим токи:
J11 = Jк2 – E4/R4 =9 – (-200)/30=15,6667 A
J22= E4/R4 + E5/R5 =(-200)/30+250/10=18,3333 A
J33 = -E5/R5=-250/10=-25 A
Составим матрицу и, используя программу Gauss, определим потенциалы точек:
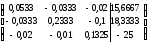
φ1=275,8275 В φ2=56,7606 В φ3=-142,7611 В
Uxx =-φ1 =-275,8275 В
Для определения Rэкв преобразуем треугольник сопротивления в звезду сопротивления:
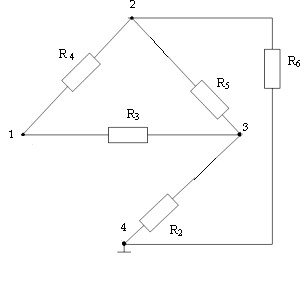
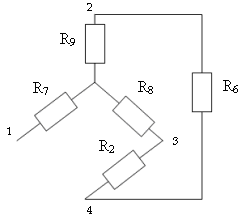
По формулам преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений определяем R7, R8 , R9 :
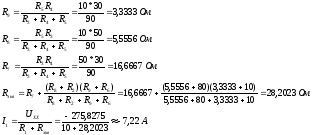
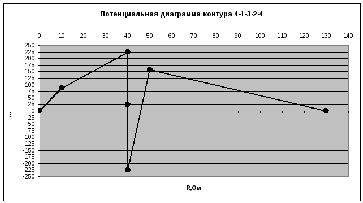
6. Потенциальная диаграмма контура 4-1-3-2-4.
φ4=0 В
φ1= φ4 – I1R1 =-(-8,659)*10=86,59 В
φ5= φ1 – I4R4 =86,59 – (-4,553)*30=223,18 В
φ2= φ5 + Е4 =223,18 + (-200)=23,18 В
φ6= φ2 – Е5 =23,18 – 250 =-226,82 В
φ3= φ6 + I5R5 =-226,82 + 6,871*10 =158,11 В
φ4= φ3 + I2R2 = 158,11 – 1,977*80 =0 В
Федеральное агентство по образованию
ГОУ ВПО
Уфимский государственный авиационный технический университет
Кафедра ТОЭ
Расчетно-графическая работа №1
по дисциплине:
Теоретические основы электротехники
«Расчет линейной электрической цепи постоянного тока»
Выполнил: студент гр. ЭСиС-307
факультета АП
Чиков В.А.
Проверил: Лукманов В.С.
Уфа-2007
