Расчетно-графическая работа №22(1)
.docЗадание
Определить закон
изменения во времени тока в цепи
классическим и операторным методами.
Построить график искомой величины на
интервале от t
= 0 до t
=
![]() ,
где
,
где
![]() - меньший по модулю
корень характеристического уравнения.
- меньший по модулю
корень характеристического уравнения.
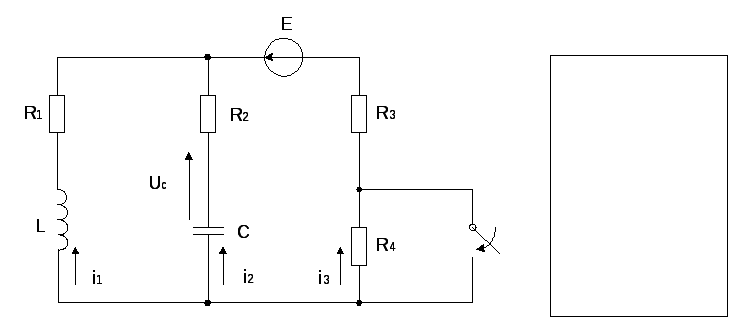
КЛАССИЧЕСКИЙ МЕТОД
Определим значения токов и напряжений непосредственно до коммутации

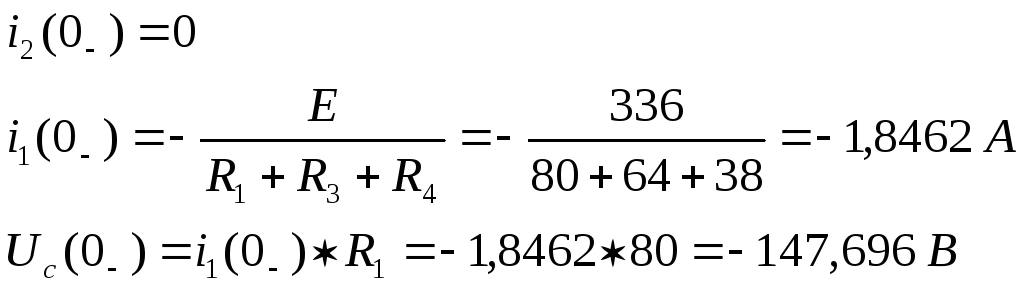
Составим характеристическое уравнение и найдем его корни


Представим искомую
величину
![]() в виде суммы
принужденной составляющей и свободной
составляющей
в виде суммы
принужденной составляющей и свободной
составляющей
![]()
Найдем принужденные составляющие токов и напряжений
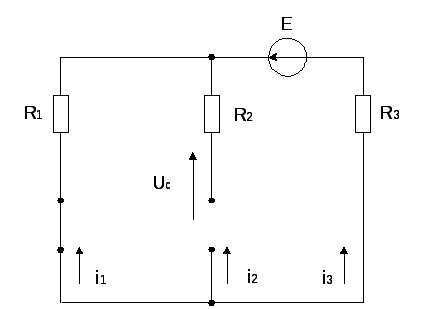
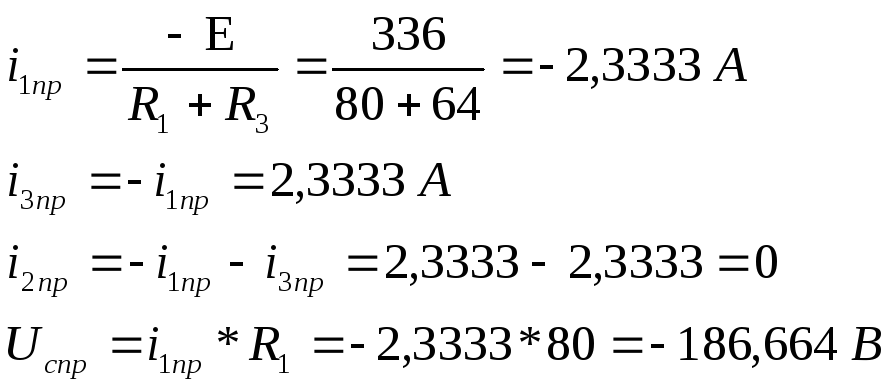
Составим дифференциальные уравнения по законам Кирхгофа для послекоммутационного режима


По законам коммутации:
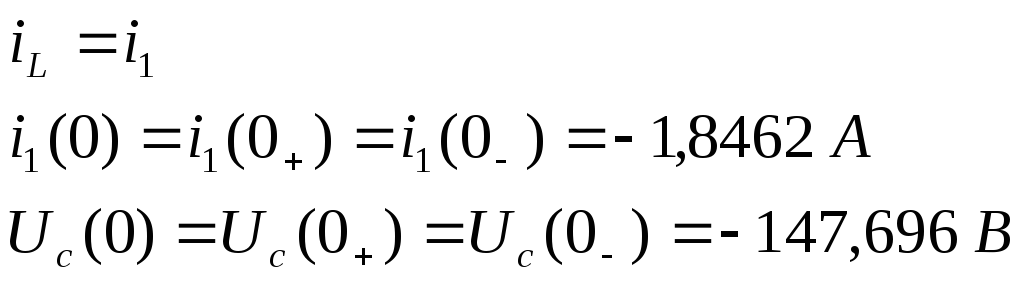
Из уравнений (1) и (3) следует:
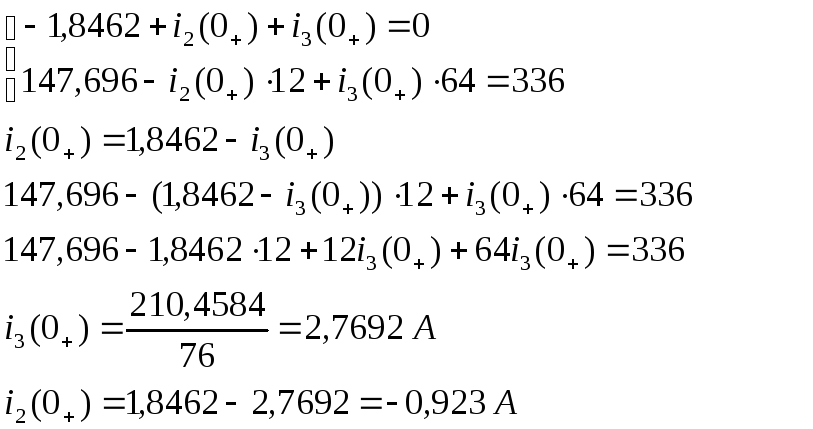
Подставим полученные
значения в уравнение (2) и найдем
![]()
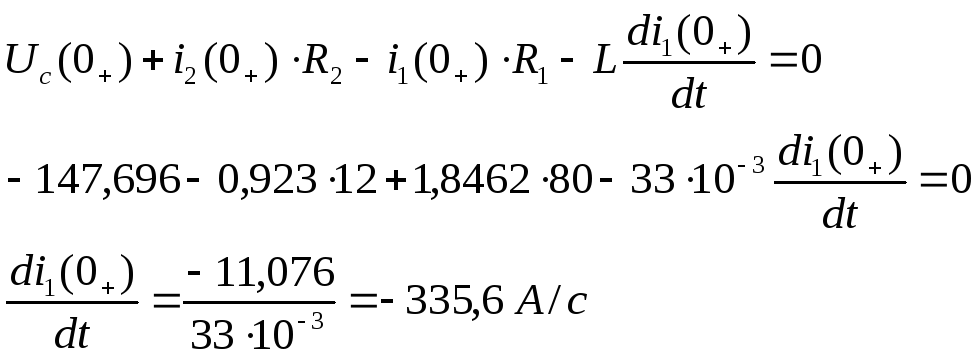
Продифференцируем
уравнения (1) и (3) и найдем
![]() и
и
![]()
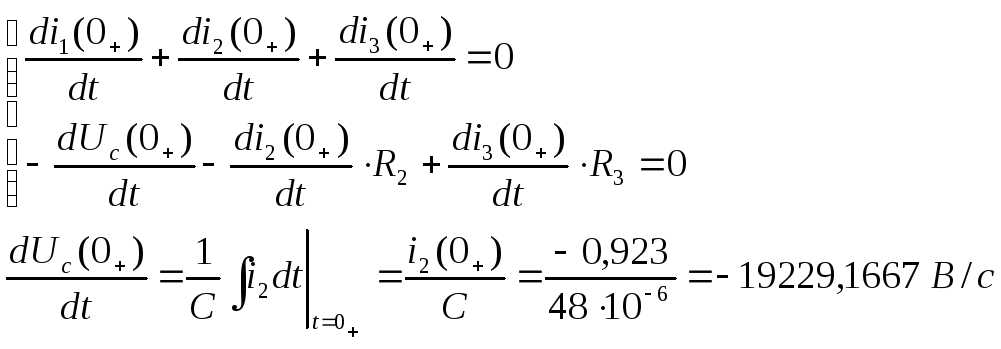
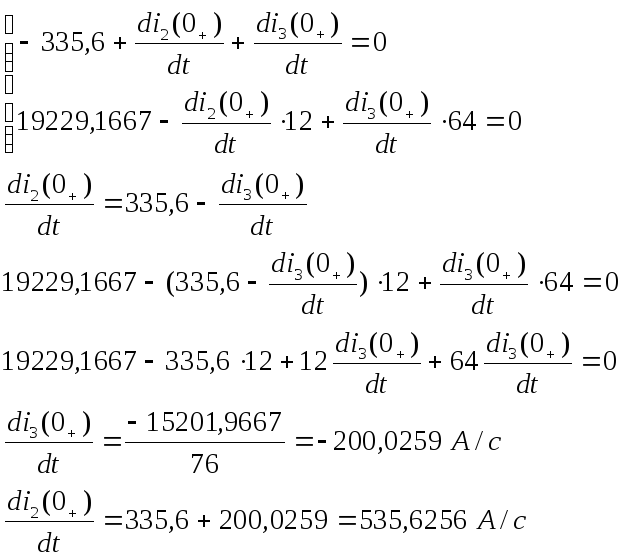
Составим систему уравнений для определения постоянных интегрирования
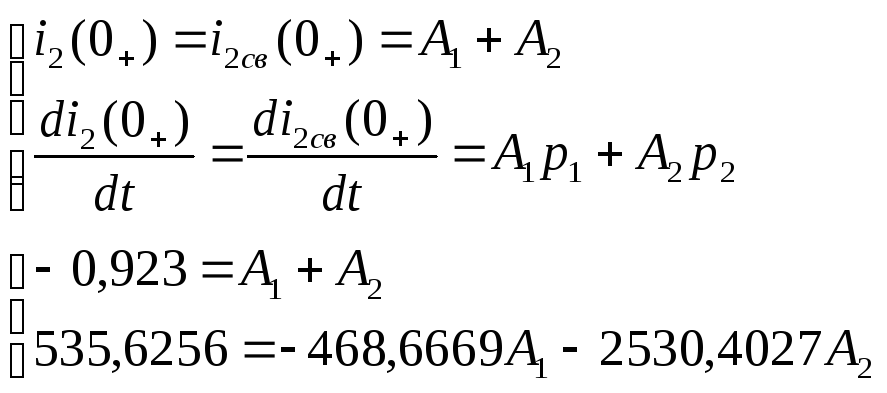

ОПЕРАТОРНЫЙ МЕТОД
Значения токов и напряжений непосредственно до коммутации
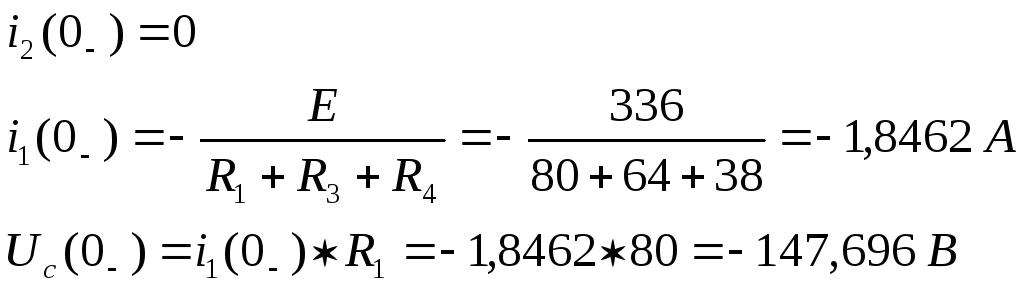
Операторная схема замещения цепи
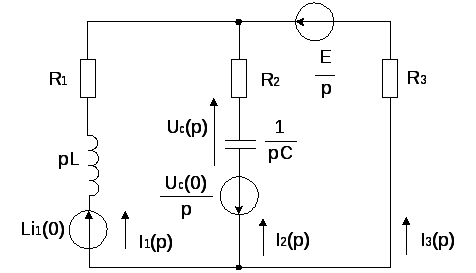
Составим систему уравнений по законам Кирхгофа в операторной форме
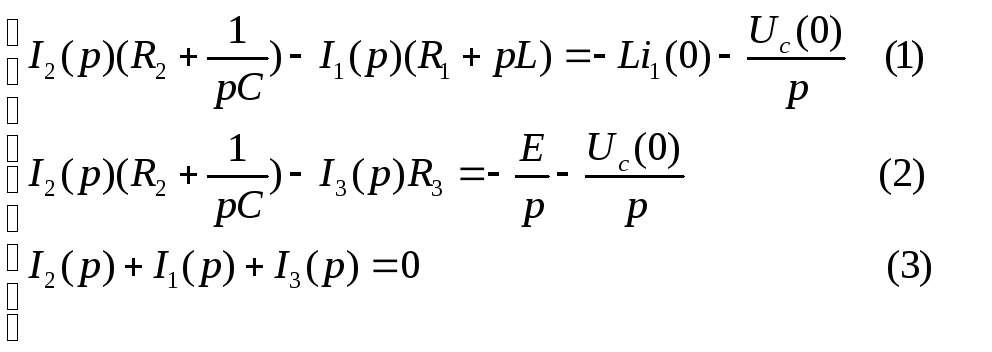
Выразим
![]() и
и![]() из
уравнений (1) и (2)
из
уравнений (1) и (2)

Подставим полученные выражения в уравнение (3)
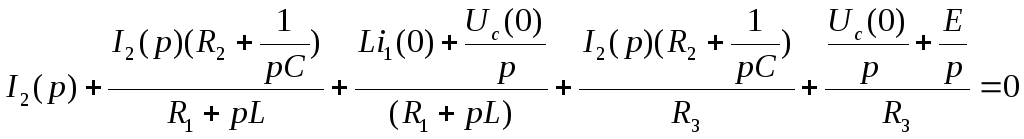

Переход от изображения к функции времени с помощью формулы разложения
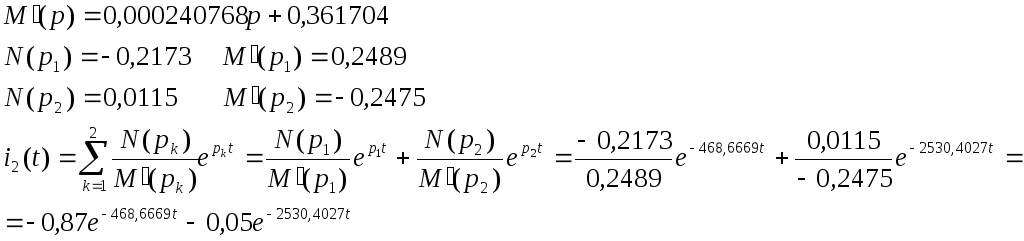
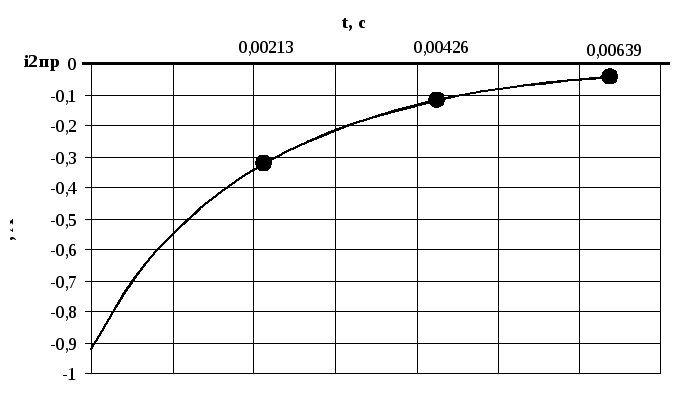
Построим график
искомой величины
![]() на интервале от t
= 0 до t
=
на интервале от t
= 0 до t
=
![]()