1.5 Постоянная времени цепи и ее физический смысл

Закон изменения множителя зависит от величины. Эта величина имеет размерность времени и называется постоянной времени цепи. Обозначается постоянная времени греческой буквой .

Через 5 после коммутации любой ток или напряжение цепи достигает 99,3% от своего предельного значения (при t ). В неразветвленной RL- цепи (рис.1.2):

(1.15)

Таким образом, имеем решение для i_L(t) при 0₊, т.е. при всех t переходного процесса:

. (1.16)

Определяем напряжение на резисторе R и индуктивности L в переходном режиме:

(1.17)

(1.18)

По формулам (1.17), (1.18) построим графики изменения напряжений от времени t.

1

2

3

4

Рис. 1.4

Из рис. 1.4 видно, что при любом значении t сумма напряжений u_R и u_L составляет величину входного напряжения U, что подтверждает второй закон Кирхгофа.

Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t=0₊ индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t, как бесконечно малое сопротивление (короткое замыкание цепи).

Постоянная времени τ – это время, в течение которого свободная составляющая i_св изменяется ровно в “e” раз. Покажем это. Для этого сравним два значения i_св при произвольном времени t, взятых через время τ:

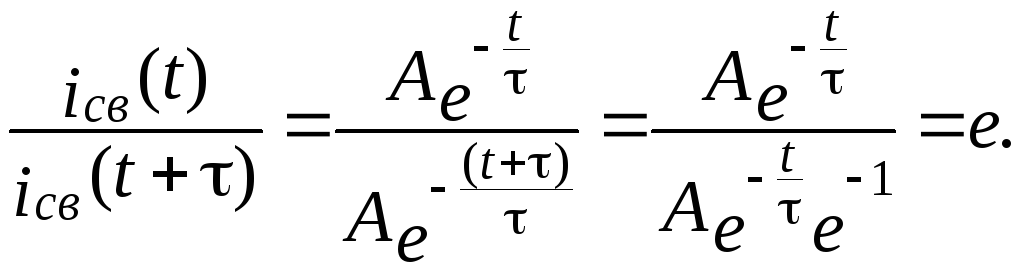
Таким образом, величина τ определяет скорость протекания переходного процесса в цепи, т.к. через (45)τ он обычно практически заканчивается.

2.Расчет прохождения сигнала через линейные электрические цепи

Параметры сигнала:

длительность импульса: 0,4 мс; период сигнала: 1,5 мс; середина импульса: 0,014 мс; максимальное и минимальное значение сигнала: 0,5 и 0 В.

2.1Разложение импульсных колебаний на гармонические составляющие

Результат воздействия на электрическую цепь синусоидального напряжения и тока можно найти при помощи символического метода решения уравнений Кирхгофа. Форма синусоидального напряжения (или тока) на выходе любой линейной электрической цепи остается синусоидальной, а амплитуда напряжений и его начальная фаза изменяются. Поэтому при рассмотрении воздействия на электрические цепи несинусоидальных напряжений (токов) во многих случаях целесообразно представить их в виде некоторой суммы синусоидальных колебаний.

Любое периодическое несинусоидальное колебание можно разложить в бесконечный тригонометрический ряд, состоящий из постоянной составляющей и синусоидальных составляющих различной частоты, амплитуды и фазы. Совокупность этих синусоидальных или гармонических составляющих называется частотным спектром.

Тригонометрический ряд, получающийся при разложении периодических несинусоидальных колебаний, называется рядом Фурье [7, с.7]:

Коэффициенты ряда Фурье ( А₀, a_k, b_k и φ_k ) рассчитываем по формулам [7, c.7]:

Где

f(t) – несинусоидальная периодическая функция;

Т – период колебаний, т.е. наименьшее время, по истечении которого колебания полностью повторяются, 1/с;

ω₁ – скорость изменения фазы (угловая частота) первой или основной гармоники, рад/с;

k – порядковый номер гармоники.

В радиотехнике для определения отклика цепи на негармоническое воздействие f(t) используют косинусную форму ряда Фурье [1, с.276]:

которая связана с рядом Фурье (2.1) следующими соотношениями [1, с.276]:

где A_mk –это амплитуда «k»-ой гармоники, функция четная относительно частоты;

φ_k – начальная фаза «k»-ой гармоники, функция нечетная относительно частоты и поэтому может принимать как положительные значения, так и отрицательные;

А₀ – постоянная составляющая воздействия f(t).

Амплитуды всех гармоник разложения (A_mk) вместе с постоянной составляющей разложения (А₀) образуют амплитудно-частотный спектр (АЧС) воздействия f(t).

Начальные фазы всех гармоник разложения (ψ_k) образуют фазо-частотный спектр (ФЧС) воздействия f(t).

Заданный импульс напряжения выражается в пределах одного периода функцией

0,5,

f(t)=

0,

т.е. мы имеем импульсное напряжение прямоугольной формы с периодом повторения Т и длительностью импульса τ_И со смещением середины импульса относительно оси ординат.

Интегрирование проводим в пределах от 0 до, введя перед интегралом множитель 2.

Постоянная составляющая ряда на основании формулы (2.2) будет равна

Коэффициенты а_k, b_k (формулы (2.3) и (2.4)) :

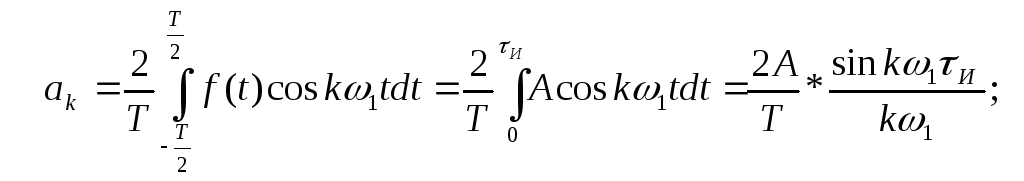
Рассчитываем коэффициенты (амплитуды гармоник) при косинусных составляющих ряда Фурье, а также начальные фазы гармоник:

Тогда

Учитывая то, что[2, c.98],

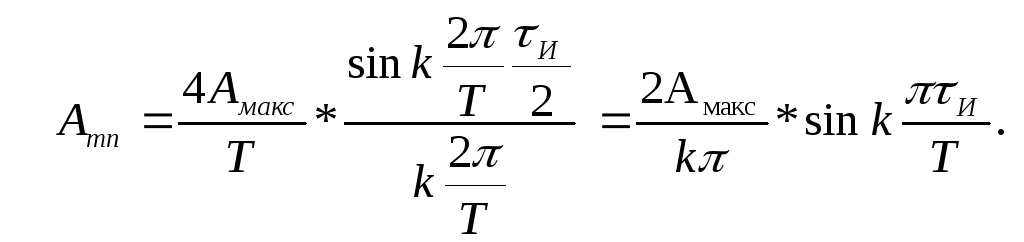
Подставляя численные значения в формулы, получим амплитуды и начальные фазы гармонических составляющих ряда Фурье.

Таким образом рассчитывают периодические колебания функций четных относительно частоты. При смещении момента отсчета времени на любую величину, т.е. при запаздывании или опережении процесса на время t₀, учитываем смещение середины импульса относительно оси ординат. Смещение периодической функции не изменяет значений амплитуд гармоник. Начальные фазы гармоник изменяются на угол [2,с.276],

где t₀ – время начала переднего фронта импульса.

t₀=-t_{смещения}= - 0,2+0,014= - 0,186,

т.е. начальные фазы гармонических составляющих сигнала воздействия рассчитываются по формуле:

.

Рассчитаем постоянную составляющую

,

и амплитуды и начальные фазы гармонических составляющих:

для первой гармоники (k=1)

для второй гармоники (k =2)

для третьей гармоники (k =3)

для четвертой гармоники (k =4)

для пятой гармоники (k =5)

для шестой гармоники (k =6)

для седьмой гармоники (k =7)

для восьмой гармоники (k =8)

для девятой гармоники (k =9)

для десятой гармоники (k =10)

Амплитудный и фазовый спектр сигнала воздействия изображен на рис. 2.1