1. Определение коэффициента взаимной индукции с применением математической модели индуктивной связи

Воспользуемся имеющейся в составе microcap математической моделью индуктивной связи и трансформатора. С помощью этой модели можно рассчитывать и анализировать любые линейные электрические цепи, индуктивно связанные между собой.

В схеме используем не только индуктивно-связанные компоненты, но и УГО (условное графическое изображение) индуктивной связи (рис. 8.12).

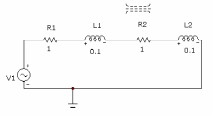
Рис. 8.12 исследуемая схема с УГО, согласное включение

Для помещения УГО: components/analog primitives/passive components/K, появляется окно с именем K. В разделе INDUCTORS указываем имена индуктивно-связанных компонентов L1 и L2, в разделе COUPLING указывается величина коэффициента индуктивной связи, М – коэффициент взаимоиндукции.

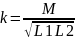, в данном случае примем k=0.5.

Рассмотрим две схемы, с согласным и встречным расположением индуктивностей рисунок 8.13

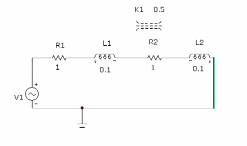
Рис. 8.13 исследуемая схема с УГО, встречное включение

Частота источника ЭДС 1000Гц, сопротивления 1 Ом индуктивность 0.1Гн, что соответствует сопротивлению 628Ом. Такое сопротивление позволяет пренебречь активным сопротивлением при расчете коэффициента взаимной индукции.

Напоминаю!

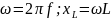
Моделируем в режиме анализа переходных процессов, результаты на рисунке 8.14 – согласное соединение, 8.15 – встречное расположение. Диапазон времени около одной минуты, шаг подберите сами.

Рис 8.14

Рис 8.15

При согласном включении амплитуда тока составляет 73,2мкА , при встречном 214,4мкА.

Пренебрегая активным сопротивление, найдем выходное индуктивное сопротивление схемы для встречного и согласного включения.

Проведем динамический частотный анализ схем (рис. 8.16), из его видно, что амплитуда напряжения на входе схемы равна 1В.

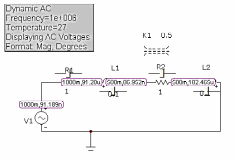
Рис. 8.16

Следовательно, сопротивление при согласном включении:

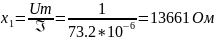
сопротивление при встречном включении:

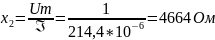
Определяем коэффициент взаимоиндукции:

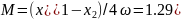
Коэффициент связи в этом случае будет равен:

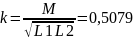
Что приблизительно совпадает с принятым при моделировании значении. Если же не совпадает, то необходимо продолжить моделирование с другим коэффициентом.

2. Моделирование схемы с несколькими индуктивно-связанными элементами и использованием модели индуктивной связи.

Рассмотрим схему, изображенную на рисунке 8.17, на ферромагнитном тороидальном сердечнике намотано три катушки, коэффициент индуктивной связи примем равным 0,95.

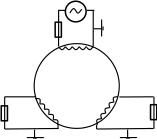
Рис. 8.17

Индуктивность катушки вычисляем по формуле

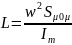
Если на сердечнике несколько катушек, то отношение индуктивностей катушек распределяется как:

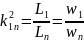
Где n=2,3… a k_1n – коэффициент трансформации катушек с номерами 1 и n.

В рассматриваемой схеме источник синусоидальной ЭДС с амплитудой 10В, частотой 1000Гц и начальной фазой 0. k₁₂=0.5, k₂₃=0.25. Схема, реализованная, в microcap представлена на рис 8.18.

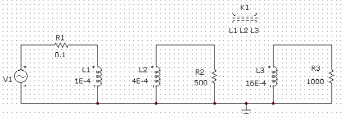
рис 8.18

Расчет схемы выполняется в режиме Анализ переходных процессов, параметры анализа устанавливаем в соответствии с рисунком 8.19

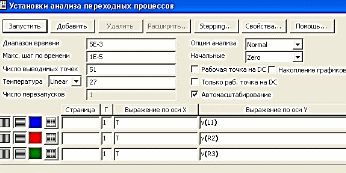
Рис. 8.19

Результаты анализа представлены на рис 8.20, на нем курсором отмечены амплитудные значения синусоидальных напряжений на катушках. V(L1)=9.786, V(R2)=18.596, V(R3)=37.056.

По результатам моделирования находим коэффициенты трансформации:

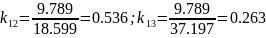
Эти значения близки к теоретическим

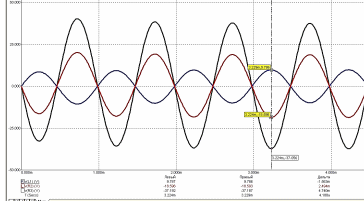
рис 8.20

Для получения статистики расчета в окне с результатами анализа нажимаем сочетание клавиш alt+z. В окне с именем статистика появится статистика анализа рис 8.21.