Моделирование резонансного режима. Расчет и построение резонансных кривых и частотных характеристик схем синусоидального тока Теоретическое введение

Электрическая цепь, содержащая индуктивность и емкость, может служить колебательным контуром, где возникает процесс колебаний электрической энергии, переходящей из индуктивности в емкость и обратно. В идеальном колебательном контуре эти колебания будут незатухающими. При подсоединении колебательного контура к источнику переменного тока угловая частота источника может оказаться равной угловой частоте, с которой происходят колебания электрической энергии в контуре. В этом случае имеет место явление резонанса, т. е. совпадения частоты свободных колебаний, возникающих в какой-либо физической системе, с частотой вынужденных колебаний, сообщаемых этой системе внешними силами.

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту источника переменного тока

индуктивность L

емкость С.

Различают резонанс при последовательном соединении L и С —резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.

Например, пусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f.

В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.

Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.

Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.

Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.

Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.

Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.

Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.

В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.

Ход выполнения работы:

Так как при последовательном соединении R, L, C элементов наблюдается резонанс напряжений, когда равны реактивные сопротивления x_c=x_L, то рассмотрим схему, показанную на рисунке 8.1, где R=10 Ом, е=Е_msin(314t). Амплитуда E=141,4 B, начальная фаза источника ЭДС_ψЕ=0, частота f=50Гц.

Моделирование резонансного режима

Резонансные параметры L и C находятся из соотношений:

Примем x_c=x_L=30Ом, тогда при ω=314 получим L=95,541мГн, С=106,15 мкФ.

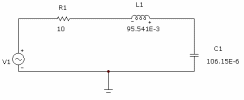
Рис. 8.1

Выполняем команды: анализ/анализ переходных процессов, устанавливаем параметры в соответствии с рисунком 8.2

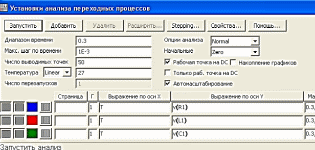
Рис. 8.2

На графиках (рисунок 8.3) зафиксированы амплитудные значения напряжения на индуктивном, емкостном и резистивном элементах.

C

L

C

R

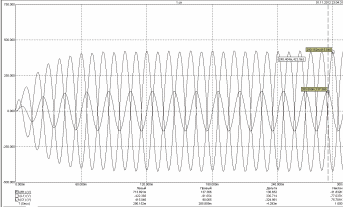
Рис 8.3

На индуктивном и емкостном элементах фазы напряжения сдвинуты друг от друга на 180°. На последнем периоде они имеют одинаковую амплитуду U_mL=U_mC=415B. На резистивном элементе U_mR=137В.

Экспериментальное значение добротности определяется:

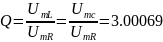
Теоретически:

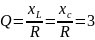
То есть microcap позволяет моделировать процессы с очень большой точностью.

Определим резонансное значение на катушке индуктивности, как результат максимального значение напряжения на резистивном элементе схемы. В панели анализа переходных процессов используем опцию stepping, где указываем варьируемый параметр (рисунок 8.4). Далее нажимаем «да» и запускаем анализ из меню «Анализ переходных процессов/выполнить анализ», далее нажимаем комбинацию клавиш ctrl+F11, появляется окно оптимизации (рисунок 8.5).

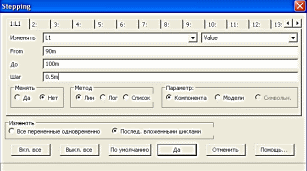
Рис. 8.4

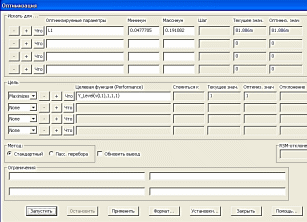
Рис. 8.5

Наблюдаем, что графики процесса изменились, а индуктивность стала равна 81,886m.

Расчет и построение резонансных кривых и частотных характеристик:

Расчет выполняется в режиме Частотный анализ. Рассмотрим схему на рисунке 8.1. Выполняем команду, появляется диалоговое окно Установки частотного анализа (рисунок 8.6).

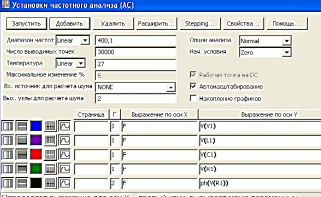
Рис 8.6

Получаем следующие графики рисунок 8.7

индуктивны характер цепи

Емкостной характер цепи

R1

V1

C1

L1

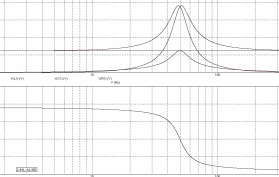
Рис 8.7

Верхний график – амплитудно-частотная характеристика, нижний – фазово-частотная. На частоте 50Гц напряжение на емкостном и индуктивном элементах составляет 3 вольта, рисунок 8.8

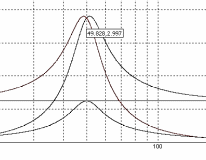
Рис 8.8

Определяем по графикам максимум напряжения на индуктивном и емкостном элементах, они составляют 3,039В на частоте 51,879Гц и 3,038В на частоте 48,099Гц соответственно. То есть добротность контура Q=3.

Теоретические значения ω_c и ω_L:

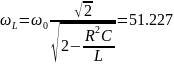
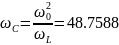
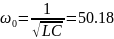
Эти расчеты совпадают с полученными при моделировании.

Рассчитаем резонансное значение тока на том же контуре:

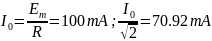
Этому уровню тока соответствую частоты f1 и f2, справа и слева от резонансной, см рисунок 8.9. Разность частот f1- f2=Δf называется полосой пропускания. Из графика вычисляем полосу пропускания и она равна: 58.068-42.295=16,791Гц.

Теоретически расчеты дают следующие результаты:

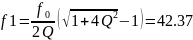
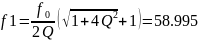
Результаты машинного расчета и теоретического практически совпадают.

Емкостной характер цепи

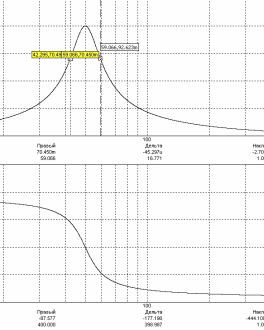
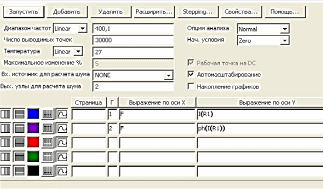
Рис 8.9

Рассмотрим изменение частотной характеристики при изменении сопротивления резистора от 2 до 10 с шагом 2, изменение сопротивления задается при помощи диалогового окна stepping рисунок 8.10.

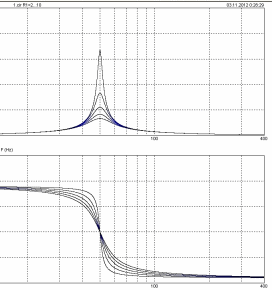
Рис 8.10

Сравним частотные характеристики для трех различных RLC – контуров.

Первый контур, представленный на рисунке 8.1, второй – рисунок 8.11а, третий – рисунок 8.11б

Резонанс напряжений

Резонанс токов

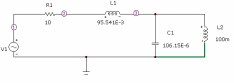
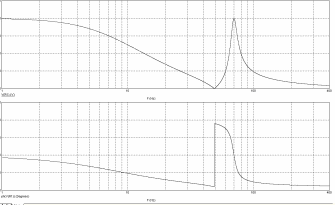
Рис 8.11 а) последовательно-параллельный контур с тремя реактивными сопротивлениями – резонанс напряжений и токов

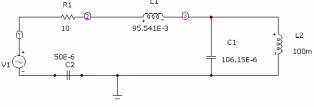
рис 8.11 б) последовательно-параллельный контур с четырьмя реактивными сопротивлениями – три резонанса, два напряжения, один – тока. Первый резонанс напряжений.

Выводы:

1. Резонансные режимы работы схемы наблюдаются только при наличии в её составе реактивных элементов

2. Количество резонансных режимов на единицу меньше числа реактивных элементов

3. резонансные режимы чередуются

4. если в схеме имеется путь для постоянного тока (рис. 8.11а), то первым будет иметь место резонанс токов.

Моделирование индуктивно-связанных цепей