Лекция 3

4. Метод интегрирования по частям неопределенного интеграла

Известно, что если , то .

Тогда взяв интегралы от обеих частей последнего равенства, получим

. Учитывая, что , получим следующую формулу

, (4.1)

или, учитывая, что ,

. (4.2)

Формулы (4.1), (4.2) называются формулами интегрирования по частям неопределенного интеграла.

Интегрирование по частям состоит в том, что подынтегральное выражение представляется в виде произведения двух множителей: и , а затем выполняются два интегрирования:

1. сначала отыскивается функция (постоянная С принимается равной нулю);

2. затем находится интеграл , который возможно, вычисляется легче, чем исходный.

При этом следует учитывать, что обычно к функции следует относить множители, которые упрощаются при дифференцировании, а все остальные множители – к , причем так, чтобы можно было найти интеграл .

Укажем некоторые виды интегралов, которые можно вычислить, используя метод интегрирования по частям ( – многочлен степени ).

Тип	Вид интеграла	Метод замены
1		, применять метод интегрирования по частям -раз, обозначая через очередную производную от
2

Пример 1. Найти .

Решение: Интеграл относится к интегралу первого типу ( ). Поэтому примем , . Тогда применяя формулу (4.1), получим

.

В некоторых случаях приходится несколько раз применять метод интегрирования по частям.

Пример 2. Найти .

Решение: Представленный интеграл относится к интегралу первого типа ( ). Вычисляем два раза формулой (4.1):

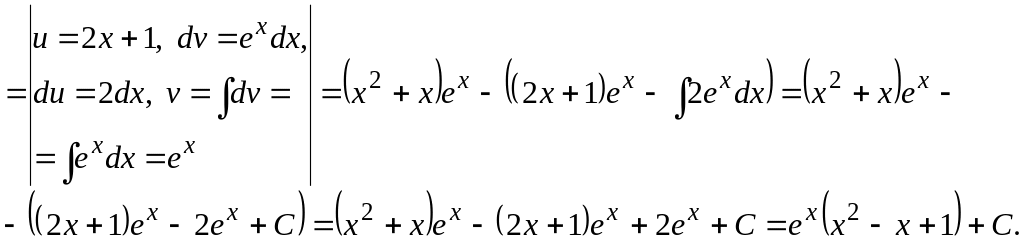
Пример 3. Найти .

Решение: Представленный интеграл относится к интегралу второго типа ( ). Вычисляем его интегрированием по частям:

.

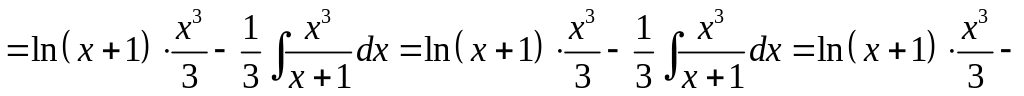
Пример 4. Вычислить .

Решение: Представленный интеграл относится к интегралу второго типа. Примем , . Тогда вычисляя по формуле (4.1), имеем

,

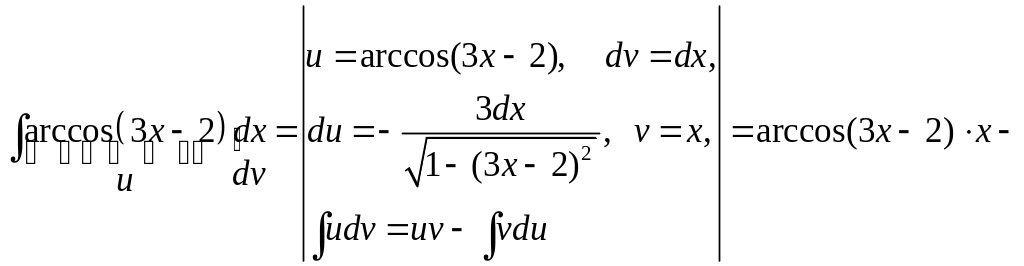
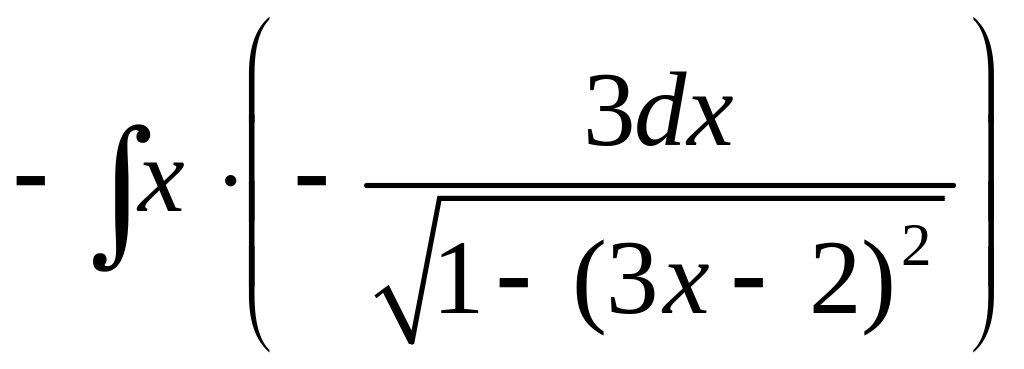
где .

Интеграл вычислим методом замены переменной (подведением под знак дифференциала). Примем , тогда , , ,

, .

Итак, окончательно имеем .

5. Интегрирование выражений, содержащих квадратный трехчлен

Интегралы вида

( ), (5.1)

( ) (5.2)

в зависимости от знака и знака дискриминанта квадратного трехчлена приводятся путем выделения полного квадрата с последующей линейной заменой к табличным интегралам Т14 – Т17.

Замечание: Без ограничения общности всегда можно считать, что коэффициент равен единице по модулю.

Пример 1. Найти интеграл .

Решение: Выделим полный квадрат квадратного трехчлена . Тогда

.

Пример 2. Вычислить интеграл .

Решение: Выделяя полный квадрат квадратного трехчлена в знаменателе,

получим . Тогда

.

Пример 3. Вычислить .

Решение: Выделение полного квадрата квадратного трехчлена дает . Тогда

.

Рассмотрим далее интегралы вида

( ), (5.3)

( ). (5.4)

При вычислении интегралов (5.3), (5.4) сначала выделяют полный квадрат в квадратном трехчлене . Затем делают линейную замену, в результате чего исходный интеграл (5.3) или (5.4) можно разбить на два интеграла, один из которых является табличным интегралом Т14 – Т17, а другой находится методом замены переменной (знаменатель берется за новую переменную).

Пример 5.4. Найти интеграл .

Решение: Выделяем полный квадрат . Тогда

.

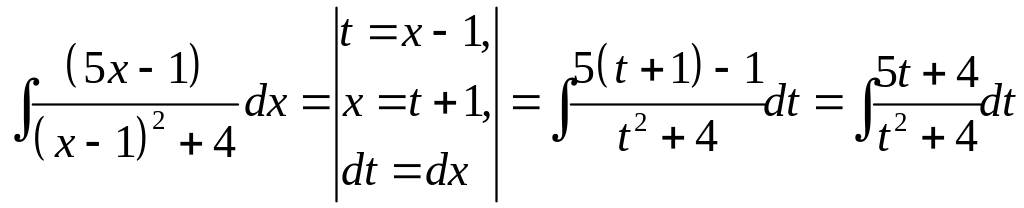Полученный интеграл разбиваем на два интеграла . Второй интеграл является табличным: .

Первый интеграл вычисляем методом замены переменной

Итак, окончательно имеем .
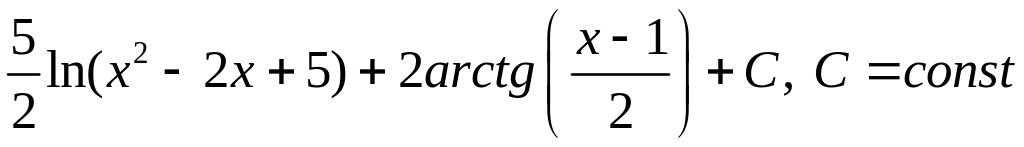