5. Обобщенный закон Ома

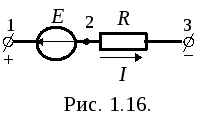
Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы. Пусть на неразветвленном участке 1-3 сложной цепи (рис. 1.15), содержащей источник и потребитель энергии, протекает ток I.

Для определения потенциала любой точки электрической цепи необходимо произвольно задать потенциал какой-нибудь одной точки. Пусть для рассматриваемой схемы . Потенциал точки 2 больше потенциала точки 1 на значение ЭДС:. ТокI в любом пассивном элементе цепи направлен от точки с более высоким потенциалом до точки с более низким потенциалом. Поэтому потенциал точки 3 меньше потенциала точки 2, т.е. .

Объединив эти две формулы, получаем:

(1.21)

Отсюда ток (1.22)

Рассуждая аналогичным образом, можно получить выражение обобщенного закона Ома для случая противодействующего источника ЭДС: (1.23)

Объединив эти две формулы в одну, получим:

, (1.24)

где верхний знак соответствует ветви с содействующим источником ЭДС, а нижний – с противодействующим. Выведенная формула представляет собой закон Ома для участка цепи с ЭДС или обобщенный закон Ома.

Если в результате расчета по формуле (1.22) ток получает отрицательное значение, это означает, что действительное направление тока противоположно выбранному направлению.

Обобщенный закон Ома можно вывести для ветви, содержащей источник тока (рис. 1.17).

Для содействующего (рис. 1.17, а) источника тока

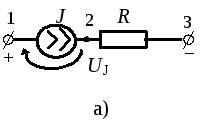
Для противодействующего (рис. 1.17, б) источника тока

Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:

(1.25)

где верхний знак соответствуют схеме, на которой U_J и J сонаправлены.

6. Баланс мощности

Прохождение электрического тока по проводнику сопровождается выделением тепла. Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию. С помощью закона Ома можно записать для потребителя с сопротивлением R:

(1.26)

Обычно под законом Джоуля-Ленца понимают уравнение, определяющее не энергию, а мощность тепловых потерь

(1.27)

В приведенных выражениях тепловая энергия и мощность выражаются в Джоулях [Дж] и Ваттах [Вт] соответственно.

Сформулированный закон распространяется на ветви, содержащие как пассивные, так и активные элементы. С этой целью пользуются обобщенным законом Ома (1.24)

(1.29)

Выражения (1.29), записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку вместоивместо.

Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:

(1.30)

Существует еще одна форма записи баланса мощности:

. (1.31)

В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–» (рис. 1.18.).

Иногда пользуются уравнением баланса мощности в арифметической форме

. (1.32)

Здесь мощности противодействующих источников считаются положительными, но при балансе учитываются как мощности потребителей.