1.3.3. Формы свободной поверхности потока при резком изменении уклона дна канала

Рассмотрим условия движения потока вблизи точки О, где имеет место «перелом» дна (рис.1.7а, б)

Будем считать, что вдали от вертикали W - W, проходящей через точку О, на левом и правом участках канала имеет место равномерный режим движения потока.

При рассмотрении этой задачи можно выделить 4 разных случая:

1) оба уклона дна канала ( и ) меньше критического (возникновение гидравлического прыжка невозможно);

2) оба уклона дна канала ( и ) больше критического (возникновение гидравлического прыжка невозможно);

3) ; (прыжок невозможен);

4) ; ; 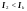здесь свободная поверхность , поднимаясь по течению, должна пересечь линию К - К ( следовательно, в русле возникает гидравлический прыжок).

15

Рис.1.7.Схемы сопряжения участков канала

Случай, когда прыжок в русле отсутствует.

Общий ход рассуждений, при помощи которого устанавливается возможная форма свободной поверхности, поясним на примере (Рис.1.8)

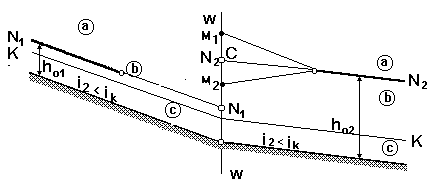
Рис. 1.8. Схемы сопряжения участков канала при отсутствии

гидравлического прыжка

16

Назовем точку пересечения искомой свободной поверхности с вертикалью W - W маркой М.

Рассмотрим возможные положения марки М на вертикали W - W:

а) марка М не может располагаться выше точки С, так как при этом для правого участка канала в зоне а получаем кривую спада, что невозможно, - в зоне а может быть только кривая подпора;

б) марка М не может располагаться ниже точки С, так как при этом для правого участка канала в зоне б получается кривая подпора, что также невозможно, - в зоне б может быть только кривая спада;

в) из сказанного выше следует, что единственно возможным положением марки М может быть совпадение ее с точкой С; при этом в пределах левого участка канала имеет место кривая подпора типа а1; в пределах правого участка канала на всем его протяжении существует равномерный режим.

Из приведенного примера дополнительно можно сделать вывод, что в случае спокойного движения воды построение кривой свободной поверхности следует вести снизу вверх, т.е. идя против течения.

На участках с бурным движением воды необходимо применять другое правило - построение кривой свободной поверхности бурных потоков следует вести в направлении вниз по течению.

Случай, когда в русле имеет место гидравлический прыжок.

Здесь бурное течение переходит в спокойное; свободная поверхность пересекает линию К - К , по одной из трех возможных схем:

а) прыжок на 1-м участке русла (рис.1.9);

б) прыжок на 2-м участке русла (рис.1.10);

в) промежуточная схема - прыжок устанавливается в месте перелома дна (рис.1.11).

Для решения вопроса о том, какая из трех схем будет иметь место в конкретном случае, рекомендуется следующая последовательность рассуждений и расчетов.

1. По соотношению h01/h02 определить тип гидравлического прыжка ( совершенный; прыжок - волна).

2. По уравнению совершенного гидравлического прыжка (1.19)

17

или по формуле (1.28) для прыжка - волны определить вторую сопряженную глубину h”, приняв значение первой сопряженной глубины прыжка равным h =h01 (рис.1.9);

3. После этого используют следующие правила:

а) если h”< h02 , то прыжок будет иметь место на первом участке канала; за прыжком будет иметь место кривая подпора с глубины h” до глубины h02 (рис.1.9);

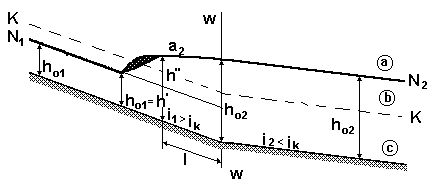
Рис.1.9. Схема сопряжения участков канала (1-й случай)

б) если h”> h02 . то прыжок будет иметь место на втором участке канала; перед прыжком будет иметь место кривая подпора с глубины h (первая сопряженная глубина относительно h”= h02) до глубины h02 (рис.1.10);

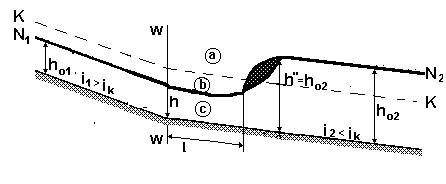
Рис.1.10. Схема сопряжения участков канала (2-й случай)

в) если h”= h02. то прыжок будет в точке О (рис.1.11);

18

Рис.1.11. Схема сопряжения участков канала (3-й случай)

Длины l, необходимые для определения местоположения прыжка определяют, используя зависимости неравномерного движения (см. ниже).

Типичные случаи кривых свободной поверхности потока при переломах дна русла и на сооружениях показаны на рис.1.12. Решая задачу по установлению форм кривой свободной поверхности, необходимо на продольном профиле русла провести линии нормальных N-N и критических K-K глубин параллельно дну на высоте hо и hк соответственно. Далее устанавливают диапазон изменения глубин пары смежных участков. В последующем, используя результаты исследования дифференциального уравнения, и типичные случаи кривых свободной поверхности строится кривая свободной поверхности в установленном диапазоне.

При построении кривой свободной поверхности потока считают, что на некоторой части бесконечно длинных участков русла устанавливается равномерное движение и глубина потока равна нормальной глубине, например в начальном и конечном сечениях рассматриваемого канала.

19

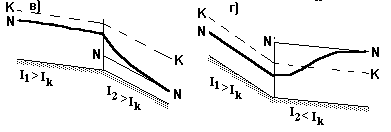
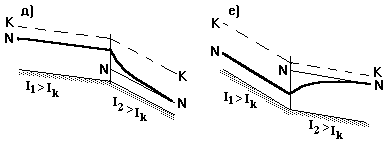
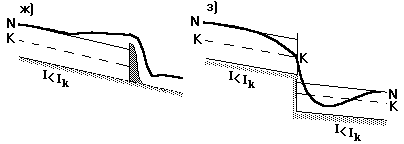
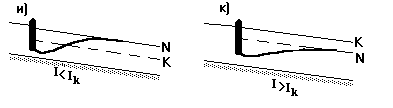
Рис.1.12. Типичные случаи форм кривых свободной поверхности.

20