- •21)Логические функции одного переменного. Нарисуйте таблицу и приведите пояснения.
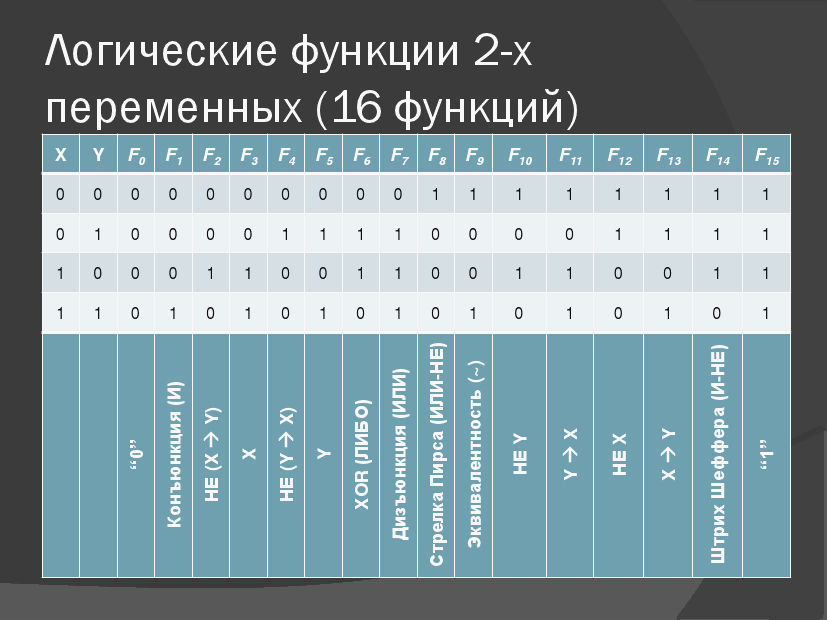
- •22)Логические функции двух переменных. Нарисуйте таблицу и приведите пояснения.
- •23)Сформулируйте понятие базиса. Объясните его смысл.
- •24)Дайте определение булевой алгебры.
- •25)Сформулируйте аксиомы булевой алгебры.
- •25)Сформулируйте законы булевой алгебры. Докажите произвольный из них.(Сходство с билетом 26, доказательство смотреть в билете 26)
- •27)Опишите принцип решения логических задач. Приведите примеры.
21)Логические функции одного переменного. Нарисуйте таблицу и приведите пояснения.
В результате выполнения любой арифметической операции над двумя двоичными
числами получается новое двоичное число. Устройство, реализующее арифметическое
действие над двоичными числами, можно рассматривать как функциональный
преобразователь, на входы которого подаются исходные двоичные числа, а с выхода в
виде двоичного числа снимается результат арифметической операции. Поскольку
отдельные разряды любого многоразрядного числа не зависят друг от друг, можно считать
аргументами указанного функционального преобразователя и его результатами не
многоразрядные двоичные числа, а отдельные разряды исходных двоичных чисел и
двоичного результата. А в этом случае устройство можно рассматривать как
функциональный преобразователь с большим числом входов и выходов, на каждом из
которых имеется один разряд числа, принимающий одно из двух значений: 0 или 1.
Переменные величины и функции от них, которые могут принимать только два
значения (например, 0 и 1), носят название логических, или булевых, переменных и
функций.
Исследованием свойств логических функций занимается математическая логика
(Булева алгебра). Познакомимся с некоторыми элементарными вопросами
математической логики.
Логические переменные-это переменные, которые принимают лишь значения 0 или1
Функцией алгебры логики, или переключательной функцией, называется такая
функция, которая как и ее аргументы принимает одно из двух значений: 0 или 1.
Запись вида (a1, а2, ..., аN), где коэффициенты аj принимают значения 0 или 1, будем
называть набором из N элементов. Количество различных наборов из N элементов
конечно и равно 2 в степени N.
Любую функцию алгебры логики или просто логическую функцию можно задать
одним из двух способов - табличным или аналитическим. Рассмотрим вначале
табличный способ.
1. Табличный способ
Таблицу, с помощью которой задают логическую функцию, называют таблицей
истинности, поскольку в математической логике логическая величина может принимать
два значения, называемые истина и ложь, а их цифровыми аналогами считаются
соответственно 1 и 0.
Функция 1. Логическое отрицание НЕ (инверсия)
Эта функция является функцией одной переменной и определяет ее инверсию. Она
истинна тогда, когда ложна переменная, и ложна, когда переменная истинна. Значения
функции задаются таблицей истинности. Таблица истинности имеет следующ
A |
¬A |
0 |
1 |
1 |
0 |
Запись "¬а" читается как "не а".

22)Логические функции двух переменных. Нарисуйте таблицу и приведите пояснения.
Функция 2. Логическое умножение (конъюнкция)
Эта функция является функцией двух переменных и истинна тогда и только тогда,
когда одновременно истинны обе входные переменные. Эта функция имеет несколько
названий. Кроме названия "логическое умножение", она называется также функцией
конъюнкции или функцией И. При использовании аналитической (формульной) записи
функция логического умножения (конъюнкции, И) изображается символом &, знаком
пересечения или точкой (как это делается при изображении операции умножения в
математике).
Запись "а&в" читается "а и в".
A |
B |
A&B |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Функция 3. Логическое сложение (дизъюнкция)
Эта функция является функцией двух переменных и истинна тогда, когда истинна
хотя бы одна входная переменная. Функция имеет несколько названий - кроме названия
"логическое сложение", она называется также функцией дизъюнкции или функцией ИЛИ.
При использовании аналитической (формульной) записи функция логического умножения
(дизъюнкции, ИЛИ) изображается символом " ∨ " или знаком объединения.
Запись "а ∨ в" читается "а или в".
A |
B |
A∨ B |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |