2. Завдання для самостійного розв’язання

1. Чи є правильним многогранником правильна піраміда?

2. Знайдіть площу поверхні правильного гексаедра, ребро якого дорівнює 0,1м.

3. Знайдіть довжину ребра правильного гексаедра, якщо площа його поверхні дорівнює 1,5 м².

4. Ребро правильного октаедра дорівнює 2. Знайдіть площу його поверхні.

Питання для самоконтролю

1. Які многогранники називають правильними?

2. Якими бувають правильні многогранники?

3. Що таке центр правильного многогранника?

4. Сформулюйте властивості правильних многогранників.

5. Де в природі зустрічаються правильні многогранники?

Завдання для самостійної роботи студентів

Модуль № 12

Тіла та поверхні обертання. Обєми тіл обертання

та площі їх поверхонь

Тема: Об’єм циліндра - 2 год.

1. Короткі теоретичні відомості та приклади

Циліндр можна розглядати як правильну кутну призму при дуже великому Наприклад, якщо дорівнює мільярду, то таку призму практично не можна відрізнити від циліндра. А об’єм такої призми дорівнює добуткові площі її основи на висоту. Тому об’єм циліндра також дорівнює добуткові площі основи на висоту.

Оскільки площа круга радіуса дорівнює , а основою циліндра є саме круг, то об’єм циліндра, радіус основи якого – а висота – , можна обчислити за формулою:

З адача 1. Знайдіть об’єм циліндра, радіус основи якого дорівнює 2 см, а висота – 5см.

Дано: Циліндр;

Знайти:

Розв’язання

см³.

Відповідь: см³.

З адача 2. Висота циліндра дорівнює 4 см, а діагональ осьового перерізу утворює з площиною основи кут 30⁰. Знайдіть об’єм циліндра.

Дано: Циліндр;

осьовий переріз циліндра;

діагональ осьового циліндра;

Знайти:

Розв’язання

.

Щоб знайти об’єм циліндра потрібно знайти його радіус.

Розглянемо - прямокутний трикутник, в якому При цьому діагональ циліндра. . Звідси Знайдемо довжину

З , за властивістю прямокутного трикутника, адже катет, що лежить проти кута дорівнює половині гіпотенузи, тоді см.

З за теоремою Піфагора

см². см.

см.

см³.

Відповідь: см³.

2. Завдання для самостійного розв’язання

1. Радіус основи циліндра дорівнює 4 см, а висота – 6 см. Знайдіть об’єм циліндра.

2. Діаметр основи циліндра дорівнює 12 см, а висота – 3 см. Знайдіть об’єм циліндра.

3. Висота циліндра дорівнює 6 см, а діагональ осьового перерізу утворює з площиною основи кут 30⁰. Знайдіть об’єм циліндра.

Питання для самоконтролю

1. Що таке циліндр?

2. Які перерізи має циліндр?

3. Чому дорівнює об’єм циліндра?

Завдання для самостійної роботи студентів

Модуль № 12

Тіла та поверхні обертання. Обєми тіл обертання

та площі їх поверхонь

Тема: Об’єм конуса - 2 год.

1. Короткі теоретичні відомості та приклади

Формулу для визначення об’єму конуса можна встановити експериментально. Пересипаючи пісок з конуса в циліндр (мал. 1) з відповідно рівними основами й висотами, неважко переконатися, що об’єм конуса втричі менший за об’єм циліндра. Отже, об’єм конуса дорівнює третині добутку площі основи на висоту.

Мал. 1

Зокрема, якщо радіус основи конуса – а висота - то його об’єм обчислюється за формулою:

Зрозуміло, що такі міркування – не доведення. Строго математично вивести формулу для визначення об’єму конуса можна за допомогою інтегралу або через об’єм піраміди.

Побудуємо два многокутники у площині основи конуса: многокутник

який містить основу конуса, і многокутник який міститься в основі конуса (мал. 2). Побудуємо дві піраміди з основами і і з вершинами у вершині конуса. Перша піраміда містить конус, а друга міститься у конусі.

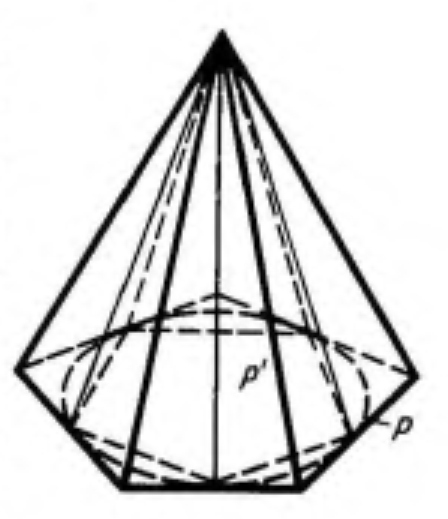
Мал. 2

Як відомо, існують такі многокутники і , площі яких при необмеженому збільшенні числа їх сторін необмежено прямують до площі круга в основі конуса. Для таких многокутників об’єм побудованих пірамід необмежено прямує до , де площа основи конуса, а його висота. Відповідно до означення, звідси випливає, що об’єм конуса

Задача 1.

Знайдіть об’єм конуса, висота якого дорівнює 3 см, а радіус основи – 1см.

Д ано: Конус;

см;

см.

Знайти:

Розв’язання

см³.

Відповідь: см³.

Задача 2. Знайдіть об’єм конуса, твірна якого дорівнює 5 м, а висота – 3 см.

Д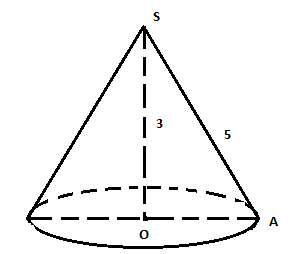 ано: Конус;

см;

твірна конуса;

см.

Знайти: .