Вопросы для самоконтроля:

1. Для чего, где и как наносятся марки углубления?

2. Имеется ли разница между осадками снятыми по маркам углубления и осадок рассчитываемых в судовой документации и в чем она заключается?

3. Что означает «запас плавучести судна»?

4. Какими конструктивными мероприятиями достигается запас плавучести судна?

5. Какими национальными и международными стандартами устанавливается запас

плавучести судна?

6. Когда и через какой период судно получает свидетельство о грузовой марке?

7. Для чего наносят и из каких частей состоит грузовая марка?

8. Каким образом и где наносится грузовая марка?

9. Что собой представляет грузовая марка?

10. Что собой представляет «гребенка», как располагается и какие марки на ней наносятся?

Тема 1.4 Начальная остойчивость судна

1.4.1. Метацентрические формулы остойчивости и их практическое применение

Как было рассмотрено выше, при малых наклонениях судна, действует пара сил, момент которой характеризует степень остойчивости.

При малых равнообъемных наклонениях судна в поперечной плоскости (Рис.21) (ЦВ перемещается в плоскости наклонения), поперечный восстанавливающий момент m_θ может быть представлен выражением:

m_θ = γV∙ ,

г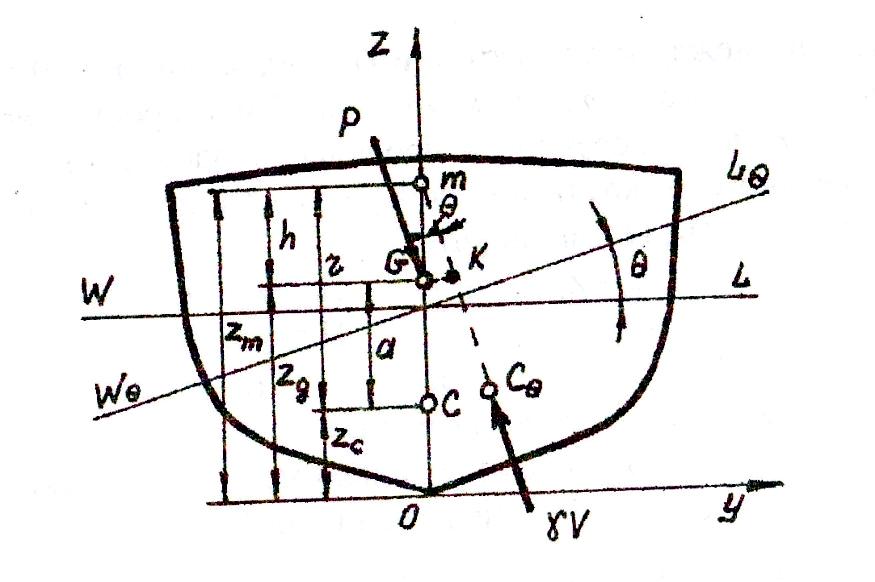 де плечо момента = ℓ_θ называют плечом статической остойчивости.

Из прямоугольного треугольника mGK находим, что ℓ_θ = h sin θ

тогда:

m_θ = ∆ h sin θ = γV h sin θ,

или учитывая малые значения θ и принимая sin θ ≈ θ⁰ / 57⁰,3 , получим метацентрическую формулу продольной остойчивости:

m_θ = γV h θ⁰ / 57⁰,3.

Рассматривая по аналогии наклонения судна в продольной плоскости (Рис.22), нетрудно получить метацентрическую формулу продольной остойчивости :

Рис.21 Поперечное наклонение судна Mψ = ∆ℓ_ψ = γV H sin ψ = γV H sin ψ⁰ / 57⁰,3

где : Mψ – продольный восстанавливающий момент, а ℓ_ψ – плечо продольной остойчивости.

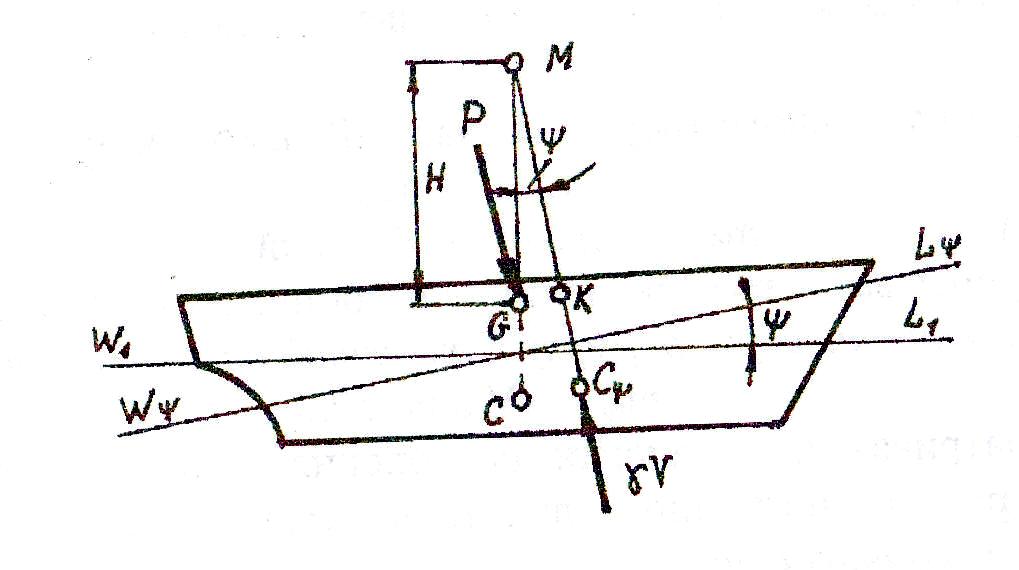
Рис. 22 Продольное наклонение судна.

На практике используют коэффициент остойчивости, являющийся произведение

водоизмещения ∆ на метацентрическую высоту h.

Коэффициент поперечной остойчивости:

К_θ = γV h = ∆h

Коэффициент продольной остойчивости:

К_ψ = γVН = ∆Н.

С учетом коэффициентов остойчивости метацентрические формулы примут вид:

m_θ = К_θ θ⁰ / 57⁰,3 , Mψ = К_ψ ψ⁰ / 57⁰,3

Метацентрические формулы остойчивости, дающие простую зависимость восстанавливающего момента от силы тяжести и угла наклонения судна, позволяют решать ряд практических задач возникающих в судовых условиях. В частности, по этим формулам можно определить угол крена или угол дифферента, который получит судно от воздействия заданного кренящего или дифферентующего момента, при известной массе и метацентрической высоте. Наклонение судна под воздействием m_кр (М_диф) приводит к появлению обратного по знаку восстанавливающего момента m_θ (М_ψ) возрастающего по величине с нарастанием угла крена (дифферента). Нарастание угла крена (дифферента) будет происходить до тех пор, пока восстанавливающий момент не станет равным по величине кренящему моменту (дифферентующему моменту), т.е. до выполнения условия:

m_θ = m_кр и М_ψ = М_диф

После этого судно будет плавать с углами крена (дифферента):

θ⁰ = 57⁰,3 m_кр / γV h = 57⁰,3 m_кр / ∆ h

ψ⁰ = 57⁰,3 М_диф / γV Н= 57⁰,3 М_диф / ∆ Н.

Полагая в данных формулах θ = 1⁰ и ψ =1⁰, найдем величины моменты кренящего судна на один градус, и момента дифферентующего судно на один градус:

m₁⁰ = γV h = 0,0175 γV h = 0,0175 ∆ h =

М₁⁰ = γV Н = 0,0175 γV Н = 0,0175 ∆ Н.

В ряде случаев используется также величина момента дифферентующего судно на один сантиметр m_д. При малом значении угла ψ, когда tgψ ≈ ψ, ψ = (d_H – d_K) / L = D_f / L.

С учетом этого выражения метацентрическая формула для продольного восстанавливающего момента запишется в виде:

М_ψ = М_диф = γV Н D_f / L.

Полагая в формуле D_f = 1см = 0,01м, получим: (

m_д = 0,01 γV Н / L = 0,01 ∆ Н / L.

При известных значениях m₁⁰, М₁⁰ и m_д, угол крена, угол дифферента и дифферент от воздействия на судно заданного кренящего или дифферентующего момента могут быть определены по простым зависимостям:

θ⁰ = m_кр / m₁⁰ ψ⁰ = М_диф / М₁⁰ D_f = М_диф /100 m_д

В приведенных выше рассуждениях предполагалось, что судно в исходном положении

(до воздействия m_кр или М_диф) плавало прямо и на ровный киль. Если же в исходном положении судна крен и дифферент отличались от нуля. то найденные значения θ⁰, ψ⁰ и D_f следует рассматривать как добавочные (δθ⁰, δψ⁰ и δD_f).

С помощью метацентрических формул остойчивости можно определить также, какой необходимый кренящий или дифферентующий момент надо приложить судну, чтобы создать заданный угол крена или дифферента (с целью заделки пробоины в бортовой обшивке, окраски или просмотра гребных винтов). Для судна, плавающего в исходном положении без крена и дифферента:

m_кр = γV h θ⁰ / 57⁰,3 = m₁⁰ θ⁰

М_диф = γV Н ψ⁰ / 57⁰,3 = М₁⁰ ψ⁰ или М_диф = 100 D_f m_д

Практически метацентрическими формулами остойчивости допустимо пользоваться при малых углах наклонения (θ 10⁰ ÷ 12⁰ и ψ 5⁰) но при условии, что при этих углах не входит в воду верхняя палуба или не выходит из воды скула судна. Они справедливы также при условии, что восстанавливающие моменты m_θ и М_ψ противоположны по знаку моментам m_кр

М_диф, т.е. что судно обладает положительной начальной остойчивостью.