4.5. Цилиндрические зубчатые передачи

4.5.1. Силы в зацеплении

Силы принято определять в полюсе W (рис.4.5) зацепления.

По линии зацепления b – b (рис. 4.5) действует нормальная сила F_n. Для удобства расчетов силу F_n принято раскладывать на три составляющие:

29

1) F_t – окружная сила, направленная по касательной к делительным окружностям. Это основная, движущая, полезная сила. На колесе z₂ F_t совпадает с направлением вращения n₂. На шестерне z₁ F направлена против вращения n₁.

Следовательно, на рис. 4.5 дана схема сил для шестерни:

F_t = 2000Т / d, (4.1)

где Т – Н∙м; d – мм;

2) F_r – радиальная сила, направленная по линии центров (радиусам). Для внешнего зацепления – к оси вращения, для внутреннего – от оси.

В торцовой плоскости t – t (рис. 4.5) имеем

F_r = tgα_t, (4.2)

где α_t – делительный угол профиля в торцовой плоскости: tgα_t = tgα_n / cosβ; α_n– нормальный угол зацепления, β – угол наклона зубьев. В практических расче-тах α_t ≈ α_n =20°.

3) F_a – осевая сила, направленная параллельно оси а – а зубчатого коле-

са. Силы F_t и F_а как составляющие нормальной силы F_n′, всегда находятся вне линии зуба (рис. 4.5). В делительной плоскости:

F_а = F_ttgβ. (4.3)

Необходимый в дальнейших расчетах основной угол наклона зуба

β_b (в основной плоскости зацепления b) определяется как β_b = arcsin(sinβcosα_n).

Полная нормальная сила (рис. 4.5):

F_n = F_nt / cosβ_b = F_t / (cosα_tcosβ_b). (4.4)

Для прямозубых передач во всех формулах β = β_b = 0; α_t = α_n = α;

F_t = 2000T / d; F_r = F_ttgα; F_a = 0; F_n = F_t / cosα.

Недостатком косозубых передач является наличие осевых сил F_а, кото-рые дополнительно нагружают опоры валов, усложняя их конструкцию.

Рис. 4.6

В косозубых передачах углы β ограничены в пределах 8…18°. Указанный недостаток устранен в шевронной передаче, которая представляет собой сдвоенную косозубую с противоположным наклоном зубьев на полушевронах. Из рис. 4.6 видно, что осевые силы Fа /2 взаимоуравновешены.

4.5.2. Расчет на сопротивление контактной усталости

Косые зубья цилиндрических колес нарезают тем же инструментом, что и прямые, установленным относительно заготовки под углом β.

Расчет на прочность принято вести для прямозубой передачи. Для этого все зубчатые и червячные передачи приводятся к эквивалентным прямозубым цилиндрическим.

Эквивалентные параметры косозубого цилиндрического колеса (приведение рассматривалось в курсе "Теория машин и механизмов"): делительный диаметр d_v = d / cos²β; эквивалентное число зубьев z_v = z / cosβ, где z – действительное число зубьев косозубого колеса.

30

С увеличением β эквивалентные параметры возрастают, способствуя повышению прочности передачи. Вследствие того, что косой зуб входит в зацеп-

ление не сразу всей длиной, он лучше прирабатывается, а большее число пар зубьев в зацеплении снижает шум и динамические нагрузки. Чем больше угол β, тем выше плавность зацепления.

Контактная прочность (σ_Н ≤ σ_НР) является основным критерием работоспособности большинства зубчатых передач.

Расчет производят в полюсе W (рис. 4.7), где имеет место наибольшая нагрузка (зона однопарного зацепления) и начинается усталостное выкрашивание зубьев.

Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n и b

Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n

с нормальными радиусами кривизны ρ_n1 и ρ_n2. Используют формулу Герца для первоначального контакта по линии:

σ_Н = Z_E(w_Hn / ρ_nv)^1/2 ≤ σ_НP. (4.5)

Напряжения σ_Н одинаковы для зубьев z₁ и z₂. Оценку сопротивления контактной усталости производят по расчетной величине допускаемого напряжения σ_НР.

В формуле (4.5): Z_E = (1 / {π[(1 – ν₁²) / E₁ + (1 – ν₂²) / E₂]})^1/2 –

– коэффициент механических свойств материалов z₁ и z₂: Е – модуль упругости; ν_{1, 2} – коэффициенты Пуассона. Для стали Е₁ = Е₂ = 2,1∙10⁵ МПа, ν₁ = ν₂ = 0,3 и

Z_Е =191,6 МПа^1/2;

w_Hn = F_nK_H / l_Σ – удельная нормальная расчетная нагрузка (на единицу длины l_Σ контактных линий), Н/мм, где K_H – коэффициент нагрузки; F_n – нормальная сила.

Вспомним, что l_Σ = b_wε_α / cosβ_b, где ε_α – торцовый коэффициент перекрытия; F_n = F_t / (cosα_tcosβ_b). Тогда получим w_Hn = F_tK_H / (b_wε_αcosα

1 / ρ_nv = 1 / ρ_n1 ± 1 / ρ_n2 – приведенная кривизна зубьев в нормальной плоскости, 1/мм.

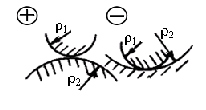
Знак плюс принимают при контакте двух вы пуклых тел (рис. 4.8), минус – выпукло (ρ1)-вог-нутых (ρ2) тел (например, внутреннее зацепление). Нормальные радиусы кривизны (рис. 4.7, б) ρn = ρt / cosβb, где из ΔONW (рис. 4.7, а) торцовый радиус ρt = dwsin αtw / 2. Выразив 1 / ρnv через параметры передачи,

п олучим , где d₁ – делительный диаметр шестерни z₁.

Подставив w_Hn и 1 / ρ_nv в формулу (4.5) и обозначив Z_ε = – коэффициент, учитывающий суммарную длину контактных линий (для прямых зубьев Z_ε = );

Z_H = – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе W, получим решение в форме ГОСТ 21354-87:

σ_Н = Z_EZ_εZ_H , (4.6)

где знак плюс – для внешнего зацепления; минус – для внутреннего.

Это формула для проверочного расчета активных поверхностей зубьев цилиндрических передач на сопротивление контактной усталости с целью предотвращения поверхностного выкрашивания.

В проектировочном расчете из условия контактной прочности определяют межосевое расстояние а_w – основной габаритный размер передачи.

Для этого в формуле (4.6) принимают Z_E = 191,6 МПа^1/2, в среднем ε_α =

= 1,6 и Z_ε = 0,8 – косые и шевронные зубья (β ≠ 0), Z_ε = 0,9 – прямые зубья (β =

= 0); α_t = α_tw = α_n = 20°, Z_Н = 2,5 – прямые зубья, Z_Н = 2,46 – косые (β = 10^О) зубья. Вводят коэффициент рабочей ширины ψ_ba зубчатого венца по межосевому расстоянию: ψ_ba = b_w / а_w , заменяя b_w = ψ_baа_w. Диаметр d₁ = 2а_w / (u ± 1). Окружная сила F_t = 2000T₁ / d₁. Тогда будем иметь

а_w′ = К_а(и ± 1) , (4.7) где К_а = Z_EZ_εZ_H , при β ≠ 0 К_а = 410 МПа^1/3, при β = 0 К_а = 450 МПа^1/3.

В формуле (4.7) а_w′, мм, Т₁ , Н∙м, σ_НР , МПа.

Расчетное значение а_w′ округляют до а_w в ближайшую большую сторону:

– для стандартных передач по ГОСТ 2185-66 (по ряду чисел R_a20);

– для нестандартных передач возможно округление до числа, кратного пяти.

Формула (4.7) главная для проектировочного расчета закрытых цилиндрических передач с целью предотвращения усталостного выкрашивания поверхностей зубьев.