2.2.3. Формула Симпсона

Пусть y = Ax² + Bx + C; x₀ = -h, x₁ = 0, x₂ = h. Рассмотрим интеграл

Имеем при x₀ = -h y₀ = Ah² - Bh + C; при x₁ = 0 y₁ = C; при x₂ = h y₂ = Ah² + Bh + C. Преобразуем 2Ah² + 6C = Ah² - Bh + C + Ah² + Bh + C + 4С = y₀ + 4y₁ + y₂. Тогда

Пусть требуется вычислить . Разобьем промежуток [a,b] на четное число равных частей. Пусть это число n = 2m. Обозначим y_k = f(x_k) значения у в точках разбиения. Тогда имеем (для x = x_j+1 - x_j):

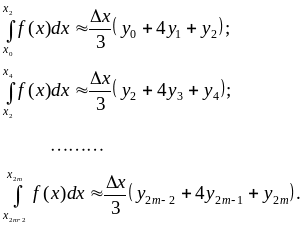
Суммируя, получим

,

где , a  z  b, f⁽⁴⁾(z) - наибольшее значение четвертой производной подынтегральной функции.

2.3. Численные методы решения дифференциальных уравнений первого порядка

Требуется найти решение задачи Коши:

при у(x₀) = y₀.

2.3.1. Метод Эйлера

Метод Эйлера прост и нагляден, хотя недостаточно практически эффективен. Заменяем производную в дифференциальном уравнении разностным отношением. Будем считать, что шаг по x равен h = const и обозначим x₁ = x₀ + h; x₂ = x₀ + 2h; x₃ = x₀ + 3h; , а приближенные значения y(x_k) = y_k. Тогда

или

Отсюда получаем

y_k+1 = y_k + hf(x_k,y_k).

Полагая k = 0,1,2, можно найти значения y₁, y₂, , т.е. получается табличное задание искомой функции.

2.3.2. Метод Рунге-Кутта

При разложении искомой функции y = f(x) в ряд Тейлора в методе Рунге-Кутта в отличие от метода Эйлера используются члены до четвертой производной. Данный метод имеет следующие достоинства:

1. хорошая точность;

2. метод является явным, т.е. значение y_k+1 вычисляется по ранее найденным значениям за определенное число действий по определенным формулам;

3. метод допускает расчет с переменным шагом;

4. для начала расчета достаточно выбрать шаг и задать значение y₀; далее (для шага h = const) вычисления идут по одним и тем же формулам:

где

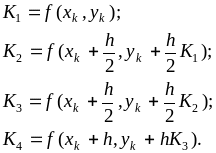
3. Пример решения задачи

Условие задачи:

вычислить значение суммы членов бесконечного ряда

с точностью до члена ряда, меньшего . Определить число членов ряда, вошедших в сумму.

Метод и алгоритм решения задачи.

Используем рекуррентное соотношение для вычисления очередного члена ряда. Для этого найдем отношение Получим

,

где а₁ = х, n = 2,3,4,

Схема алгоритма, реализующего предложенный метод, представлена на рис.7, где а - очередной член ряда, s - текущая сумма ряда, n - текущий номер члена ряда.

Текст программы на языке Паскаль имеет вид:

PROGRAM PR3;

VAR X,E,A,S:REAL; {E - абсолютная погрешность}

N:INTEGER;

BEGIN

WRITELN (‘ВВЕДИТЕ Х,E’);

READ (X,E);

A:=X;

S:=0;

N:=1;

WHILE ABS(A) >= E DO

BEGIN

S:=S+A;

N:=N+1;

A:=-A*X*X/((2*N-2)*(2*N-1))

END;

WRITELN(‘СУММА РЯДА=’,S);

WRITELN(‘ЧИСЛО ЧЛЕНОВ РЯДА=’,N)

END.

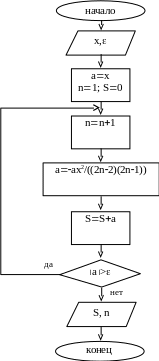
Рис.7. Блок-схема алгоритма

4. Задачи, выносимые на практические занятия

Для каждой из ниже перечисленных задач предлагается разработать алгоритм и программу.

1. Найти предел последовательности {a_n},где , принимая за него такое значение a_n, при котором |a_n-a_n-1|<.

2. Вычислить ln(1+x) с относительной погрешностью %, используя разложение в ряд:

3. Вычислить y=xⁿ+xⁿ⁺¹+...+x+1+x^-1+... с точностью до члена ряда, меньшего . Текущий член ряда вычислять, используя рекуррентную формулу.

4. Вычислить значение корня уравнения с точностью до  методом дихотомии.

5. Вычислить значение корня уравнения с точностью до  методом простых итераций.

6. Вычислить значение корня уравнения с точностью до  методом простых итераций.

7. Вычислить значение корня уравнения x+cos(x^0.52+2)=0 c точностью до  методом касательных.

8. Вычислить значение корня уравнения tg(0,3x+0,4)=x² с точностью до  методом хорд.

9. Вычислить значение корня уравнения 2x³-3x²-12x+10=0 с точностью до  комбинированным методом.

10. Вычислить интеграл по формуле прямоугольников с абсолютной погрешностью 0,001.

11. Вычислить интеграл по формуле трапеций с абсолютной погрешностью 0,001.

12. Вычислить интеграл по формуле Симпсона с абсолютной погрешностью 0,0001.

13. Методом Эйлера решить дифференциальное уравнение на интервале [a,b] с заданным y₀(a). Шаг h вводится.

14. Методом Рунге-Кутта решить дифференциальное уравнение на интервале [a,b] с заданным y₀(a) и h.

15. Найти экстремум функции y=x²-5sinx с точностью до  , используя метод касательных для производной этой функции.