2.1.3. Метод касательных

Пусть х₀ - нулевое приближение корня. Разложим f(x) по степеням (x-x₀) в ряд Тейлора:

.

Линеаризуем уравнение:

Тогда или в общем виде

(2)

Метод касательных имеет следующий геометрический смысл (рис.2).

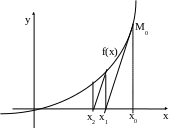
Рис.2. Метод касательных

Построим график f(x).

Рассмотрим на графике точку M₀(x₀,f(x₀)) и проведем касательную к М₀. Уравнение касательной

Найдем точку х₁. Тогда (так как y=0) и отсюда

Метод касательных всегда приводит к цели, если х₀ не лежит слишком далеко от . Возможно применение такого варианта метода:

где все наклонные прямые проводят параллельно касательной в точке М₀.

Метод касательных - частный случай метода простых итераций, где Поэтому метод сходится, когда т.е. Можно доказать, что итерации сходятся к корню с той стороны, с которой

(3)

Таким образом, алгоритм данного метода имеет следующий вид. Выделяется корень в [a,b]. Проверяется (3). Рассчитывается (2). Если |x_n+1 - x_n| < , то вычисления прекращаются.

2.1.4. Метод хорд

Если заменить производную в (2) разностью, получим итерационную формулу метода хорд:

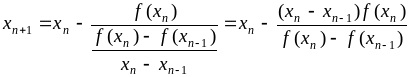(4)

Геометрический смысл метода хорд представлен на рис.3.

Метод хорд является двухшаговым, так как требует запоминания х_n и x_n-1. Можно доказать, что итерации сходятся к корню с той стороны, с которой

(5)

Таким образом алгоритм данного метода имеет следующий вид. Выделяется корень в [a,b]. Задается x₀=a, x₁=b и вычисляется x₂ по (4). Проверяется x₂ на (5). Если (5) выполняется, то берется новый интервал [x₂,b], иначе [a,x₂] и x₁=a. Если |x_n+1 - x_n| < , то вычисления заканчиваются.

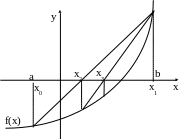
Рис.3. Метод хорд

2.1.5. Комбинированный метод

Если рассматриваемый участок графика не имеет изломов и точек перегиба, то метод хорд и метод касательных дают точки, расположенные по разные стороны от искомого корня.

Рис.6 поясняет комбинированный метод, где а₁ строится по методу хорд, а b₁ - по методу касательных.

Таким образом, получается двустороннее приближение к корню и новый интервал [a₁,b₁]. Сходимость метода очень высока. Критерий прекращения вычислений:|b_n - a_n| < 2.

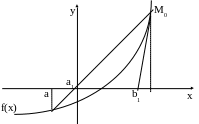
Рис.4. Комбинированный метод

2.2. Приближенное вычисление определенного интеграла

2.2.1. Формула прямоугольников

Пусть требуется вычислить . Разобьем отрезок [a,b] на n частей. Если в качестве исходных точек выбрать левые концы этих частей (рис.5), то приближенное значение J_n определенного интеграла:

где y_i = f(x_i) и x_i+1 - x_i = x для любых i.

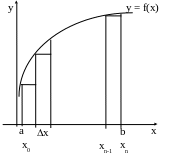
Рис.5. Метод прямоугольников

Если в качестве исходных точек выбрать правые концы частей разбиения, то

На практике обычно принимают Если соответствующую ординату обозначить как , то

,

где R_n - остаточный член, определяющий погрешность  и вычисляемый по формуле

,

где a  z  b и - наибольшее значение второй производной подынтегральной функции.

2.2.2. Формула трапеций

Разобьем отрезок [a,b] на n равных частей. Подсчитаем значение f(x) в точках x_k: f(x_k)=y_k. Тогда по формуле площади трапеции (рис.6)

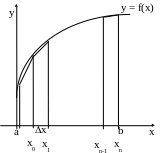
Рис.6. Метод трапеций

Суммируя, получаем

где , a  z  b и имеет тот же смысл, что и в формуле прямоугольников.