8. Преобразование треугольника сопротивлений в эквивалентную звезду и обратное преобразование

При расчете разветвленных цепей и, особенно, при определении их входных сопротивлений может возникнуть вопрос о преобразовании треугольника сопротивлений в эквивалентную звезду или обратного преобразования. Такая процедура становится возможной при условии неизменности потенциалов на зажимах преобразуемого участка цепи.

Рассмотрим участок цепи, соединенный треугольником (Рис. 3 .48).

Составим уравнения по первому и второму законам Кирхгофа для «треугольника».

Рис.3.48. Взаимное преобразование «треугольника» в «звезду»

По первому закону Кирхгофа:

«1 узел»: ;

«2 узел»: .

По второму закону Кирхгофа:

.

Решим эту систему уравнений, например, относительно тока :

Определим напряжение :

в схеме «треугольник»:

;

в схеме «звезда»:

Причем, должно выполняться такое равенство: . Приравнивая эти выражения, получим формулы перехода от соединения сопротивлений «треугольником» к сопротивлениям «звезды»:

.87(3.80)

Покажем на примере применимость данного преобразования.

Рис.3.49. Преобразование «треугольника» сопротивлений в «звезду»

Рис.3.50. Преобразование «звезды» сопротивлений в «треугольник»

Обратное преобразование из «звезды» в «треугольник» выполняется по формуле перехода:

88(3.81)

9. Метод эквивалентного генератора (активного двухполюсника)

Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.

Пусть дана некоторая электрическая цепь, которую представим активным двухполюсником (Рис. 3 .51). Необходимо рассчитать ток в ветви ab:

1) введем в ветвь abдва источника ЭДС.иодинаковые по величине и противоположно направленные:

;

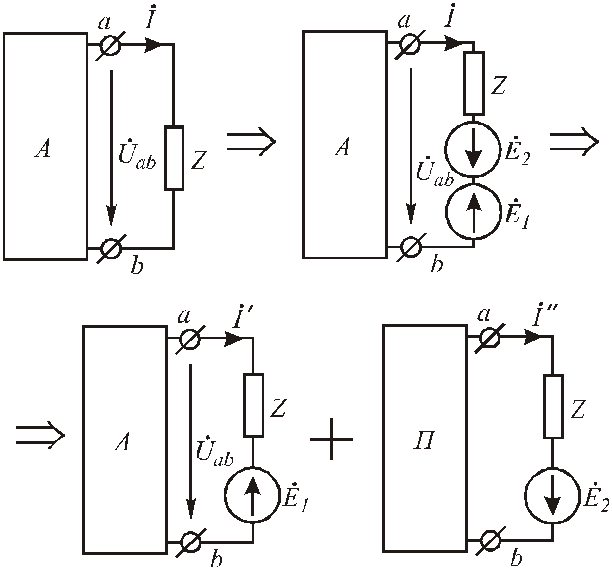
Рис.3.51. Преобразование исходного двухполюсника в сумму двух цепей

2) используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС . Вторая цепь представляет собой пассивный двухполюсник и источник ЭДС.

На основании принципа наложения ток ветви ab:

;

;.

Поскольку – любые по величине, то подберем их значения такими, чтобы токбыл равен нулю. Для этого выберем.

Напряжение на зажимах источника в режиме холостого хода численно равна его ЭДС. Тогда активный двухполюсник с источником может быть представлен в виде:

Рис.3.52. Схема замещения активного двухполюсника

В этой схеме эквивалентная ЭДС активного двухполюсника:

и, следовательно, ток

.

Таким образом, ток в ветви ab:

.89(3.82)

Пусть дана цепь (рис.2.12), рассчитаем ток методом эквивалентного генератора.

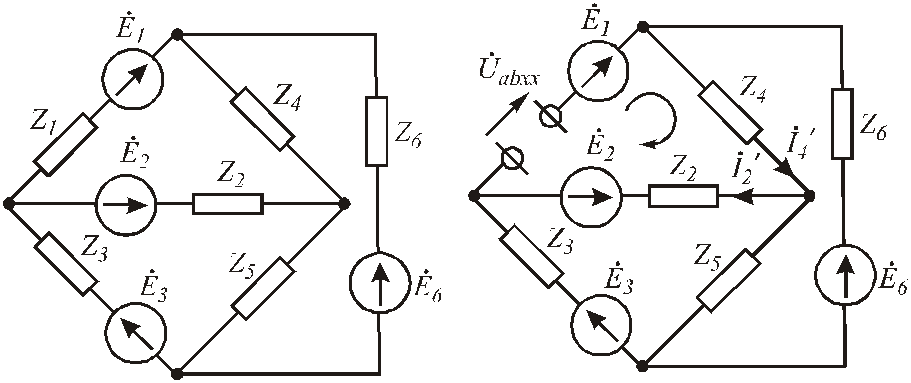
Рис.3.53. Исходная цепь

Последовательность расчета:

1. Разомкнем ветвь с сопротивлением Z₁или примемZ₁ =  .

2. Зададим положительное направление и для произвольно выбранных положительных направлений токов, например, первого контура, запишем уравнение по второму закону Кирхгофа:

.

3. Токи ив преобразованной схеме (Рис. 3 .54) рассчитываем любым известным методом, например, методом контурных токов:

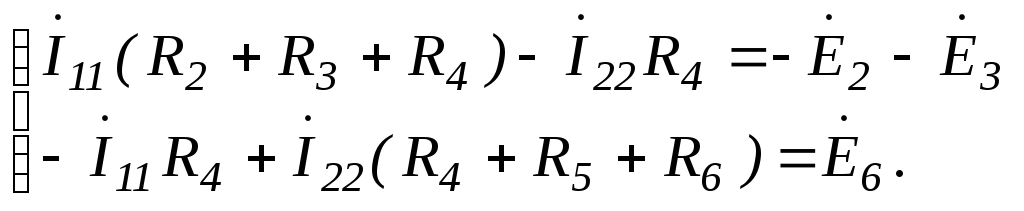
Тогда ;.

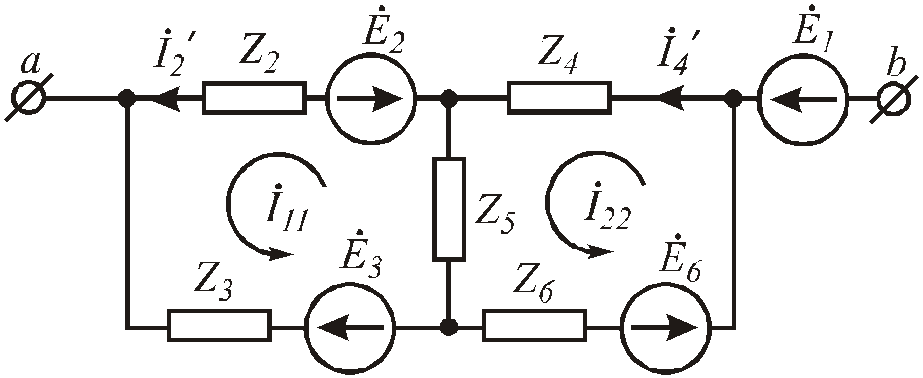
Рис.3.54. Преобразованная цепь

4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя для реальных источников их внутренние сопротивления.

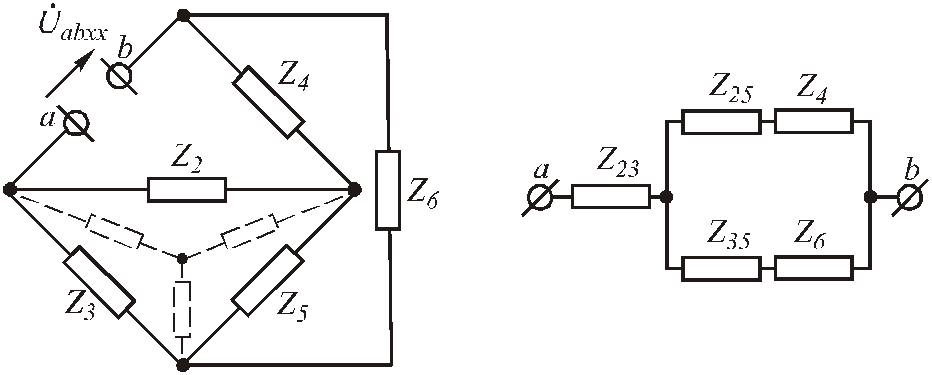
Рис.3.55. Схема пассивного двухполюсника

В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов a-b, так как нет последовательно-параллельного соединения приемников, поэтому необходимо выполнить преобразование какого-либо участка цепи из «треугольника» в «звезду» или выполнить обратное преобразование.

Заменим, например, треугольник сопротивлений Z₂–Z₃–Z₅в звездуZ₂₃–Z₂₅–Z₃₅. При этом получится схема с последовательно-параллельным соединением приемников (Рис. 3 .55.в).

Сопротивления этой схемы:

и эквивалентное сопротивление:

.

Окончательно:

.