4. Метод двух узлов

Этот метод является частным случаем метода узловых потенциалов.

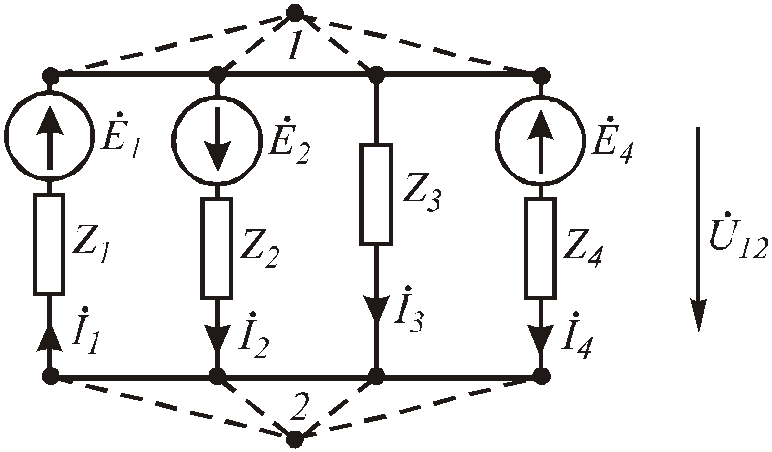
Рис.3.43. Разветвленная цепь с двумя узлами

Для вывода метода выполним следующие рассуждения. Пусть, к примеру, ₁ > ₂, тогдаU₁₂убывает от узла 1 к узлу 2.

;

.84(3.77)

Для произвольно выбранных направлений токов имеем:

;

;

;

.

Проверка правильности полученных результатов осуществляется по первому закону Кирхгофа.

5. Принцип наложения, метод наложения

Используя метод контурных токов, можно получить обобщенное уравнение по расчету любого i-го контурного тока. Сомножитель передимеет размерность Ом ^{– 1}, то есть уравнение будет иметь следующий вид:

.85

В общем случае это уравнение применимо для любого i-го контурного тока, однако, оно справедливо и для любого реального тока в ветви, так как всегда можно систему независимых контуров выбрать так, чтобы ток ветви численно равнялся контурному току. Если в уравнении (2.8) учесть, что контурная ЭДС есть сумма всех ЭДС контура, то, перегруппировав слагаемые таким образом, чтобы каждая ЭДС умножалась на соответствующую сумму слагаемых вида, получим уравнение для тока ветви.

(3.78)

В правой части уравнения (3.11) имеем сумму слагаемых – токов, созданных каждой из ЭДС ветви в отдельности.

Принцип наложения:ток любойi-ой ветви равен алгебраической сумме токов, созданных каждой из ЭДС цепи в отдельности.

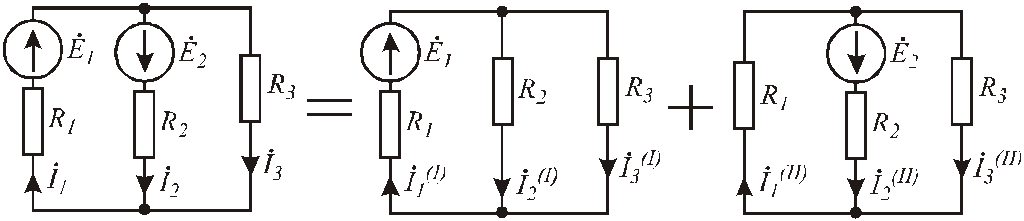
Рис.3.44. Иллюстрация принципа наложения

На сформулированном принципе базируется метод наложения, суть которого состоит в следующем: в исходной электрической цепи поочередно закорачиваются все источники ЭДС, кроме одного и производится расчет частичных токов в ветвях любым из известных методов.

Для определения реальных токов в исходной цепи производится алгебраическое суммирование этих частичных токов:

;

;

.

6. Входные и взаимные проводимости

Пусть дана некоторая электрическая цепь, содержащая единственный источник ЭДС в k-ой ветви. Кроме того, выделим еще одну ветвь –m-ю, а всю оставшуюся часть электрической цепи представим в виде некоторого пассивного четырехполюсника (Рис. 3 .45).

Рис.3.45. Схема пассивного четырехполюсника

Определим k-й иm-й токи. Используя уравнение (3.11), запишем выражение дляk-го иm-го токов:

;

.

Если E_k =1В, то;;

k-й иm-й токи численно равны своим проводимостям, при условии, чтоE_k =1В.Y_kk– входная проводимостьk – ой ветви.Y_kn– взаимная проводимостьk – ой иm - ой ветви. Рассмотрим пример определения входных и взаимных проводимостей (Рис. 3 .46).

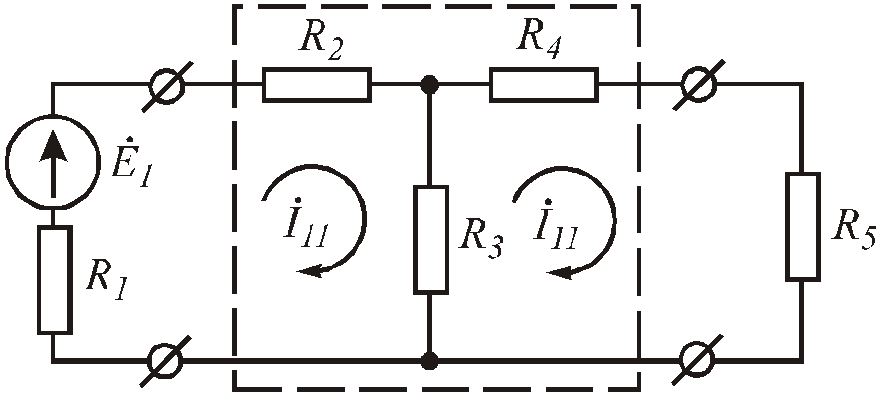
Рис.3.46. Схема замещения пассивного четырехполюсника

Представим пассивный четырехполюсник в виде схемы Рис. 3 .46 и составим для нее уравнения по методу контурных токов.

;

;

;

;

;

.

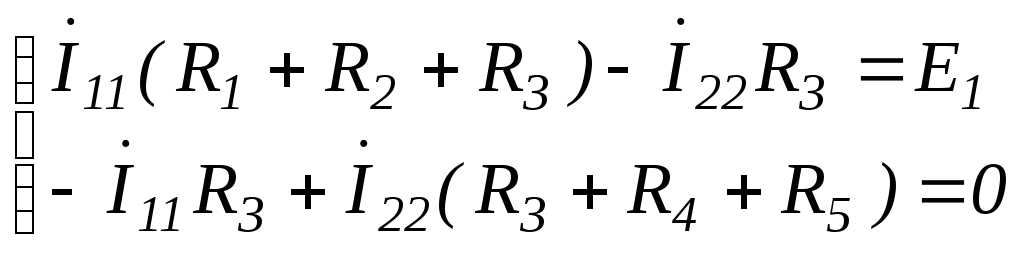7. Свойство взаимности

Рассмотрим еще одно важное свойство, имеющее место в сложных цепях, присущее линейным электрическим цепям, базирующееся на понятиях входных и взаимных проводимостей.

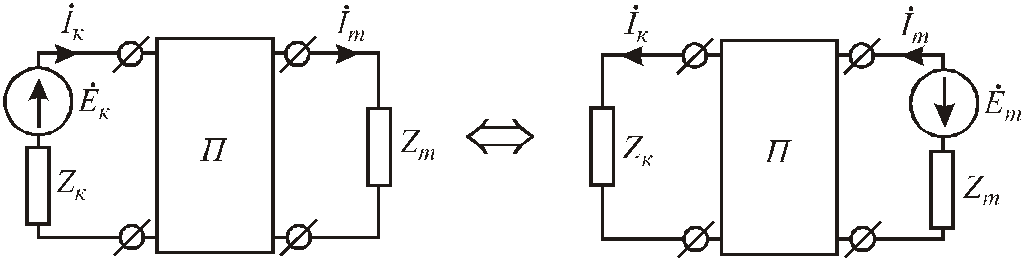
Рис.3.47. Схемы, иллюстрирующие принцип взаимности

;

.

Докажем, что взаимные проводимости Y_kkиY_knравны. Пусть для некоторой многоконтурной схемы составлена система уравнений по методу контурных токов, и главный определитель системы имеет вид:

Этот определитель всегда симметричен относительно первой главной диагонали, проходящей через элементы Z₁₁ – Z_nn, т.к. любой элементZ_km=Z_mk(сопротивления, расположенные на границеk-ого иm-ого контуров). У такого определителя строкаmне отличается от столбцаkи поэтому алгебраические дополнения, полученные вычеркиваниемk-ой строки иm-ого столбца и наоборот, равны, следовательно:

.86(3.79)

Пусть и;

Свойство взаимности:если ЭДСk-ой ветви вызывает вm-ой ветви токI_m, то, будучи перенесенным вm-ю ветвь, этот же источник вызовет ток той же амплитуды и фазы вk-ой ветви.

Цепи, обладающие такими свойствами, носят название обратимых цепей. Все линейные цепи обратимы.