I. Классическая механика Галилея-Ньютона Общие соображения

Сначала некоторые общие соображения. В том случае, когда можно полагать, что время передачи сигнала бесконечно велико (когда скорости тел малы по сравнению со скоростью передачи сигнала, т.е. по сравнению со скоростью света c= см/с, а время передачи сигнала мало по сравнению с исследуемыми промежутками времени) прекрасно работает классическая механика; она с высочайшей степенью точности позволяет вычислять движение планет Солнечной системы, спутников и ракет. Система отсчета может состоять из декартовой системы координат (например) и одних часов, находящихся в любой точке.

Теперь нужно выбрать такую систему отсчета, в которой законы механики (вообще – законы природы) описываются самым простым образом.

Пример 1. Уравнение эллипса имеет наиболее простой вид в том случае, если ось x совпадает с осью a эллипса, ось y совпадает с осью b эллипса, а начало координат совпадает с центром эллипса: - уравнение эллипса в главных осях.

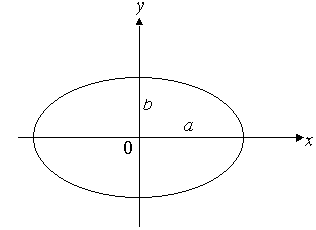
РИС. 2-1

Пример 2. В геоцентрической системе планетной системы Птолемея траектории движения планет Солнечной системы имели весьма сложный вид. В гелиоцентрической системе Коперника они же оказались простыми эллипсами.

Основные законы механики (законы Ньютона) позволяют выделить из всех систем отсчета те, в которых не только законы механики, но и все законы природы будут выглядеть особенно просто.

Представим себе, что мы выбрали некоторую систему отсчета (или системы отсчета, так как их, вообще говоря, множество), в которой материальная точка, не подверженная действию внешних сил, будет двигаться равномерно и прямолинейно, т.е. двигаться по инерции, т.е. сохранять свое состояние покоя или равномерного прямолинейного движения, пока и поскольку она не будет выведена из этого состояния вследствие взаимодействия с другими телами. Такая система отсчета называется инерциальной (инерциальная система отсчета - ИСО).

Определения и приближения

1. Материальной точкой будем называть тело, размерами которого в условиях данной задачи можно пренебречь, например:

- радиус электрона ~10^-13 см мал по сравнению с радиусом электронной орбиты ~10^-8см;

- радиус Земли =6.410³ км мал по сравнению с радиусом земной орбиты 1.510⁸ км;

- можно пренебречь диаметром Солнечной системы при рассмотрении ее движения в Галактике; и т.д.

2) Систематизация сил

Как исключается действие внешних сил, обусловленных другими телами?

Несколько слов о систематизации сил. Различают:

а) короткодействующие силы (силы взаимодействия между элементарными частицами, в том числе ядерные силы) ; характерные расстояния , на которых действуют эти силы, составляют ~10^-12 см; классическая (в смысле не квантовая) механика рассматривает только макроскопические задачи, поэтому короткодействующими силами можно пренебречь;

б) дальнодействующие силы , например:

гравитационная ( -взаимодействующие массы);

кулоновская ( - взаимодействующие заряды).

Экспериментально установлено, что дальние тела Вселенной не создают на Земле заметных статических гравитационных полей, вопрос о существовании в земных пределах переменных гравитационных полей (гравитационных волн) остается пока открытым. Земное тяготение можно исключить, создав условия невесомости .

От электрического и магнитного взаимодействия можно избавиться, или взяв немагнитное незаряженное тело, либо путем экранирования.

Известны также способы в сильной степени ослабить действие силы трения (сопротивления) , , путем разумного выбора скорости движения .

Таким образом, действие внешних сил можно исключить и, значит,

ИСО может быть реализована на практике.

Предположение о существовании ИСО эквивалентно первому закону механики Галилея-Ньютона – закону инерции.

Покажем, что ИСО не может двигаться с ускорением.

Р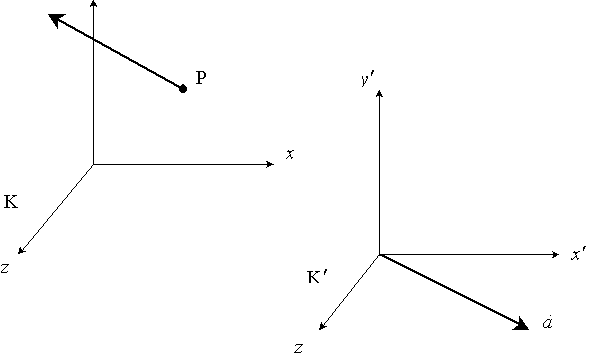 ассмотрим систему отсчета K, в которой материальная точка покоится, т. е. находится в состоянии, когда на нее не действуют никакие силы (точнее, сумма всех сил равна нулю, ).

РИС. 2-2

Если рассматривать точку из другой системы K’, движущейся относительно системы K с ускорением , то материальная точка, рассматриваемая из системы K’, будет двигаться относительно нее с ускорением - . Таким образом, наблюдатель из системы K’ будет полагать, что на точку действует сила , а этот вывод противоречит эксперименту.

Значит: 1) система K’ – неинерциальная;

2) в неинерциальной системе отсчета несправедливо представление об отсутствии сил (появляется сила инерции).

Если система K’ движется относительно K с постоянной скоростью, то точка в системе K будет двигаться относительно K’ тоже с постоянной скоростью. Сказанное справедливо по отношению к любой системе и т.д., если эти системы движутся с постоянной скоростью, т.е. все они являются ИСО. Следовательно, ИСО - бесконечное множество.

Если мы знаем хотя бы одну ИСО, то все остальные системы отсчета, движущиеся относительно первой равномерно и прямолинейно, тоже будут ИСО.

Реализация ИСО

Система отсчета, привязанная к поверхности Земли, не является инерциальной, так как из-за вращения Земли возникает дополнительное центробежное ускорение.

Для точки на экваторе: ускорение ,

период обращения Земли вокруг своей оси =86400 с,

круговая частота рад/с=0.710^-4 с^-1,

радиус Земли км = 6.4 10⁸ см, = 3.2 см/с².

Именно на эту величину ускорение силы тяжести на экваторе меньше, чем на полюсе.

Экспериментально установлено, что с высокой степенью точности инерциальной является система отсчета, начало декартовых координат которой находится в центре Солнца, а оси направлены на систему неподвижных звезд.

Инерциальные системы отсчета выделяются из других не только в механике, но, например, в электродинамике: неподвижный или движущийся с постоянной скоростью (без ускорения) заряд не излучает, а движущийся с ускорением излучает электромагнитные волны.